Question and Answers Forum
Question Number 48460 by mr W last updated on 24/Nov/18

Commented by mr W last updated on 24/Nov/18
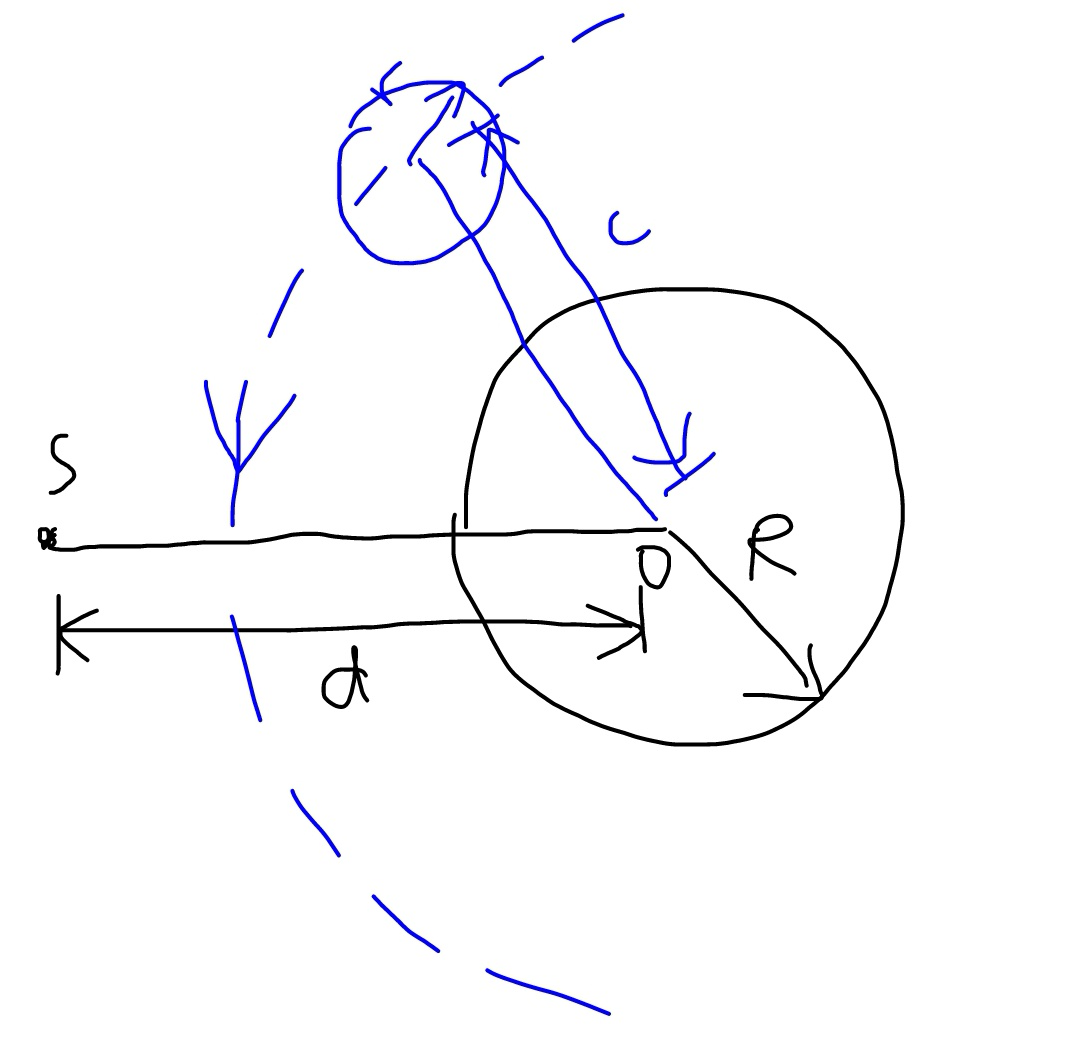
Commented by ajfour last updated on 24/Nov/18
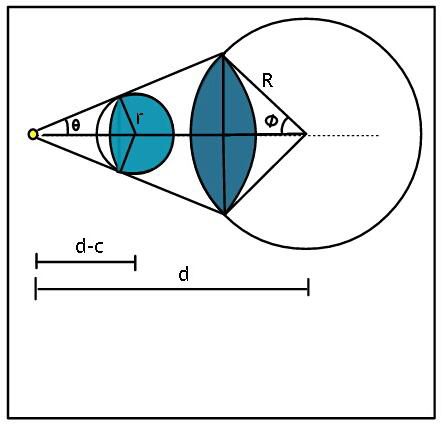
Answered by ajfour last updated on 24/Nov/18
![sin θ = (r/(d−c)) tan θ = ((Rsin φ)/(d−Rcos φ)) = λ (say) ⇒ dsin θ = R(sin φcos θ+cos φsin θ) ⇒ Rsin (φ+θ) = dsin θ φ = sin^(−1) ((rd)/(R(d−c)))−sin^(−1) (r/(d−c)) ....(i) shadow area on bigger sphere be S = ∫_0 ^( φ) (2πRsin ϕ)(Rdϕ) ⇒ S = 2πR^( 2) (1−cos φ) ...(ii) S = 2πR^2 [1−cos (sin^(−1) ((rd)/(R(d−c)))−sin^(−1) (r/(d−c)))] .](Q48487.png)
Commented by mr W last updated on 24/Nov/18

Commented by mr W last updated on 24/Nov/18