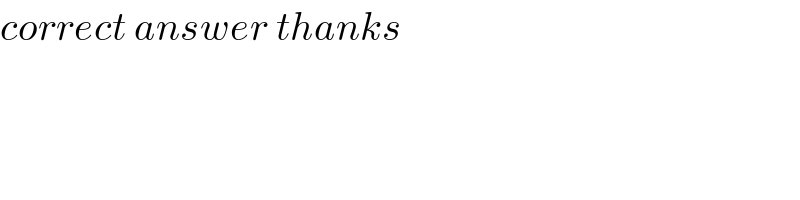let S_n =Σ_(k=1) ^n (k^2 /((2k−1)(2k+1))) 1) determine S_n interms of n 2) find lim_(n→+∞) S


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 48493 by maxmathsup by imad last updated on 24/Nov/18

$l e t S_{n} = \sum_{k = 1}^{n} \frac{k^{2}}{(2 k - 1) (2 k + 1)}$ $1) d e t e r m i n e S_{n} i n t e r m s o f n$ $2) f i n d {l i m}_{n \to + \infty} S_{n}$
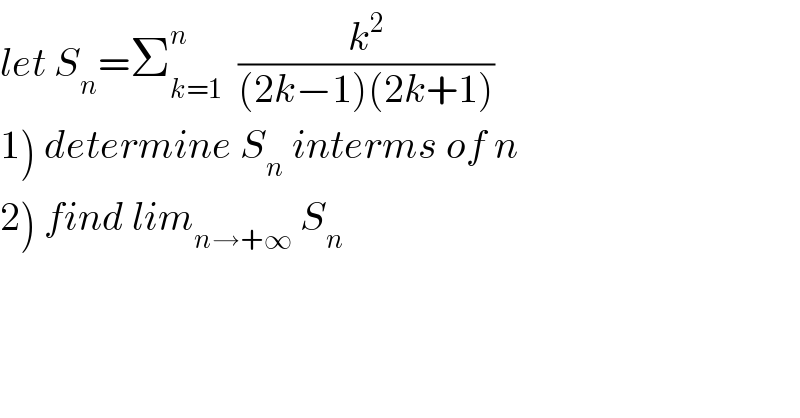
Commented by maxmathsup by imad last updated on 25/Nov/18

$1) f i r s t l e t d e c o m p o s e F (x) = \frac{x^{2}}{(2 x - 1) (2 x + 1)} \Rightarrow$ $F (x) = \frac{x}{4} (\frac{1}{2 x - 1} + \frac{1}{2 x + 1}) = \frac{1}{8} (\frac{2 x}{2 x - 1} + \frac{2 x}{2 x + 1})$ $= \frac{1}{8} (\frac{2 x - 1 + 1}{2 x - 1} + \frac{2 x + 1 - 1}{2 x + 1}) = \frac{1}{8} (1 + \frac{1}{2 x - 1} + 1 - \frac{1}{2 x + 1})$ $= \frac{1}{4} + \frac{1}{8} (\frac{1}{2 x - 1} - \frac{1}{2 x + 1}) \Rightarrow S_{n} = \frac{n}{4} + \frac{1}{8} \sum_{k = 1}^{n} \frac{1}{2 k - 1} - \frac{1}{8} \sum_{k = 1}^{n} \frac{1}{2 k + 1}$ $b u t \sum_{k = 1}^{n} \frac{1}{2 k + 1} =_{k + 1 = j} \sum_{j = 2}^{n + 1} \frac{1}{2 j - 1} = \sum_{j = 1}^{n} \frac{1}{2 j - 1} - 1 + \frac{1}{2 n + 1} \Rightarrow$ $S_{n} = \frac{n}{4} + \frac{1}{8} \sum_{k = 1}^{n} \frac{1}{2 k - 1} - \frac{1}{8} (\sum_{k = 1}^{n} \frac{1}{2 k - 1} - 1 + \frac{1}{2 n + 1})$ $= \frac{n}{4} + \frac{1}{8} - \frac{1}{8 (2 n + 1)}$ $2) i t s c l e a r t h a t {l i m}_{n \to + \infty} S_{n} = + \infty .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 24/Nov/18

	$1) \frac{k^{2}}{(2 k + 1) (2 k - 1)}$ $= \frac{1}{4} [\frac{4 k^{2} - 1 + 1}{(2 k + 1) (2 k - 1)}]$ $= \frac{1}{4} [1 + \frac{1}{2} \times \frac{(2 k + 1) - (2 k - 1)}{(2 k + 1) (2 k - 1}]$ $T_{k} = \frac{1}{4} + \frac{1}{8} [\frac{1}{2 k - 1} - \frac{1}{2 k + 1}]$ $T_{1} = \frac{1}{4} + \frac{1}{8} [\frac{1}{1} - \frac{1}{3}]$ $T_{2} = \frac{1}{4} + \frac{1}{8} [\frac{1}{3} - \frac{1}{5}]$ $T_{3} = \frac{1}{4} + \frac{1}{8} [\frac{1}{5} - \frac{1}{7}]$ $. . .$ $. . .$ $T_{n} = \frac{1}{4} + \frac{1}{8} [\frac{1}{2 n - 1} - \frac{1}{2 n + 1}]$ $a d d t h e m$ $S_{n} . = \frac{n}{4} + \frac{1}{8} [1 - \frac{1}{2 n + 1}]$ $w h e n n \to \infty$ $S_{n} = \infty + \frac{1}{8} [1 - 0] = \infty$ $p l s c h e c k . . .$
	Commented by maxmathsup by imad last updated on 25/Nov/18

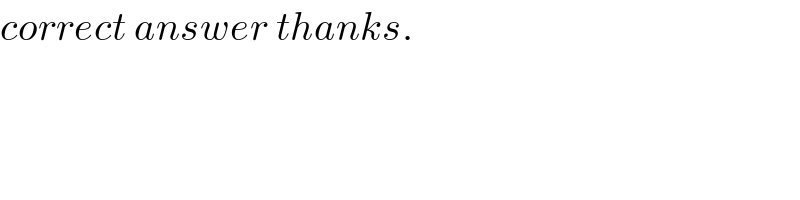
	$c o r r e c t a n s w e r t h a n k s .$
	Answered by ajfour last updated on 25/Nov/18

	$S_{n} = \underset{k = 1}{\sum^{n}} \frac{k^{2}}{(2 k - 1) (2 k + 1)}$ $= \frac{1}{4} Σ \frac{k [(2 k + 1) + (2 k - 1)]}{(2 k - 1) (2 k + 1)}$ $4 S_{n} = Σ \frac{k}{2 k - 1} + Σ \frac{k}{2 k + 1}$ $8 S_{n} = Σ (1 + \frac{1}{2 k - 1}) + Σ (1 - \frac{1}{2 k + 1})$ $= 2 n + (\frac{1}{1} + \frac{1}{3} + . . + \frac{1}{2 n - 1})$ $- (\frac{1}{3} + \frac{1}{5} + . . . + \frac{1}{2 n + 1})$ $S_{n} = \frac{n}{4} + \frac{1}{8} (1 - \frac{1}{2 n + 1}) .$
	Commented by maxmathsup by imad last updated on 25/Nov/18

	$c o r r e c t a n s w e r t h a n k s$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum