Question Number 48498 by maxmathsup by imad last updated on 24/Nov/18
$${find}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{{n}} {xdx}\:\:{and}\:{B}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{{n}} {xdx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{6}} {xdx}\:{and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{6}} {xdx}\:. \\ $$
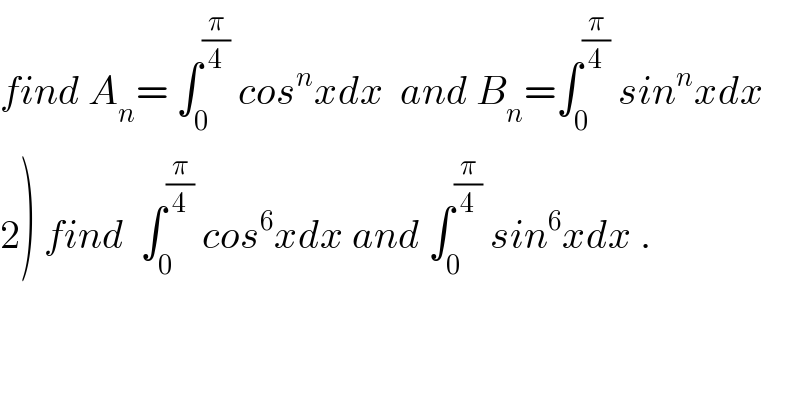
Commented by Abdulhafeez Abu qatada last updated on 24/Nov/18
$$ \\ $$$$ \\ $$$$ \\ $$$${i}\:{made}\:{an}\:{error},\:{but}\:{its}\:{corrected} \\ $$
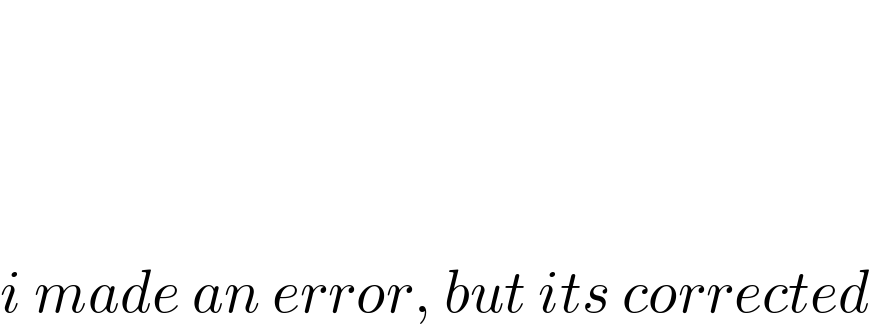
Commented by maxmathsup by imad last updated on 25/Nov/18
![1) W_n =∫_0 ^(π/4) (((e^(ix) +e^(−ix) )/2))^n dx =(1/2^n ) ∫_0 ^(π/4) (e^(ix) +e^(−ix) )^n dx =(1/2^n ) ∫_0 ^(π/4) (Σ_(k=0) ^n C_n ^k (e^(ix) )^k (e^(−ix) )^(n−k) )dx =(1/2^n ) Σ_(k=0) ^n C_n ^k ∫_0 ^(π/4) e^(ikx) e^(−i(n−k)x) dx =(1/2^n ) Σ_(k=0) ^n C_n ^k A_k A_k =∫_0 ^(π/4) e^((ik−in +ik)x) dx =∫_0 ^(π/4) e^((2ik−in)x) dx =∫_0 ^(π/4) e^(i(2k−n)x) dx =∫_0 ^(π/4) cos(2k−n)x dx +i ∫_0 ^(π/4) sin(2k−n)x dx =[(1/(2k−n))sin(2k−n)x]_0 ^(π/4) −i [(1/(2k−n)) cos(2k−n)x]_0 ^(π/4) =(1/(2k−n))sin(2k−n)(π/4) +i ((1/(2k−n)) −(1/(2k−n)) cos(2k−n)(π/4)) ⇒ W_n =(1/2^n ) Σ_(k=0) ^n C_n ^k (1/(2k−n)){sin(2k−n)(π/4) +i(1−cos(2k−n)(π/4))} =(1/2^n ) Σ_(k=0) ^n C_n ^k ((sin(2k−n)(π/4))/(2k−n)) +i (1/2^n ) Σ_(k=0) ^n C_n ^k ((1−cos(2k−n)(π/4))/(2k−n)) but W_n is real ⇒ (1/2^n ) Σ_(k=0) ^n ((1−cos(2k−n)(π/4))/(2k−n)) =0 and W_n =(1/2^n ) Σ_(k=0) ^n C_n ^k ((sin(2k−n)(π/4))/(2k−n)) .](Q48604.png)
$$\left.\mathrm{1}\right)\:{W}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\frac{{e}^{{ix}} \:+{e}^{−{ix}} }{\mathrm{2}}\right)^{{n}} {dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({e}^{{ix}} \:+{e}^{−{ix}} \right)^{{n}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\left({e}^{{ix}} \right)^{{k}} \:\left({e}^{−{ix}} \right)^{{n}−{k}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{e}^{{ikx}} \:{e}^{−{i}\left({n}−{k}\right){x}} {dx}\:\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{A}_{{k}} \\ $$$${A}_{{k}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{e}^{\left({ik}−{in}\:+{ik}\right){x}} {dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:{e}^{\left(\mathrm{2}{ik}−{in}\right){x}} {dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{e}^{{i}\left(\mathrm{2}{k}−{n}\right){x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{k}−{n}\right){x}\:{dx}\:+{i}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}\left(\mathrm{2}{k}−{n}\right){x}\:{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}{sin}\left(\mathrm{2}{k}−{n}\right){x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−{i}\:\left[\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}\:{cos}\left(\mathrm{2}{k}−{n}\right){x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}{sin}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\:\:+{i}\:\left(\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}\:{cos}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$${W}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \frac{\mathrm{1}}{\mathrm{2}{k}−{n}}\left\{{sin}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\:+{i}\left(\mathrm{1}−{cos}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:{C}_{{n}} ^{{k}} \:\:\frac{{sin}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}}{\mathrm{2}{k}−{n}}\:+{i}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}}{\mathrm{2}{k}−{n}}\:{but}\:{W}_{{n}} {is}\:{real}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}}{\mathrm{2}{k}−{n}}\:\:=\mathrm{0}\:{and}\:{W}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\frac{{sin}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}}{\mathrm{2}{k}−{n}}\:. \\ $$
Commented by maxmathsup by imad last updated on 25/Nov/18
![we have B_(n ) =∫_0 ^(π/4) (((e^(ix) −e^(−ix) )/(2i)))^n dx =(1/((2i)^n )) ∫_0 ^(π/4) (Σ_(k=0) ^n C_n ^k (e^(ix) )^k (−1)^(n−k) (e^(−ix) )^(n−k) dx =(1/((2i)^n )) Σ_(k=0) ^n C_n ^k (−1)^(n−k) ∫_0 ^(π/4) e^(ikx) e^(−i(n−k)x) dx =(1/((2i)^n )) Σ_(k=0) ^n (−1)^(n−k) C_n ^k .A_k with A_k =∫_0 ^(π/4) e^((ik−in+ik)x) dx =∫_0 ^(π/4) e^(i(2k−n)x) dx =∫_0 ^(π/4) cos(2k−n)x dx +i∫_0 ^(π/4) sin(2k−n)x dx =[(1/(2k−n))sin(2k−n)x]_0 ^(π/4) +i[−(1/(2k−n))cos(2k−n)x]_0 ^(π/4) =(1/(2k−n))sin(2k−n)(π/4) +(i/(2k−n))( 1−cos(2k−n)(π/4)) ⇒ B_n =(1/((2i)^n )) Σ_(k=0) ^n (−1)^(n−k) C_n ^k (1/(2k−n)){ sin(2k−n)(π/4) +i(1−cos(2k−n)(π/4))} ⇒B_(2n) = (1/(2^(2n) (−1)^n )) Σ_(k=0) ^(2n) (−1)^k C_(2n) ^k (1/(2k−2n)){sin(k−n)(π/2) +i(1−cos(k−n)(π/2))} but B_(2n) is real ⇒ B_(2n) =(((−1)^n )/2^(2n+1) ) Σ_(k=0) ^(2n) (−1)^k C_(2n) ^k ((sin(k−n)(π/2))/(k−n)) and we follow the same method to find B_(2n+1)](Q48605.png)
$${we}\:{have}\:{B}_{{n}\:} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}}\right)^{{n}} {dx}\:=\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{{n}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({e}^{{ix}} \right)^{{k}} \left(−\mathrm{1}\right)^{{n}−{k}} \:\left({e}^{−{ix}} \right)^{{n}−{k}} {dx}\right. \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(−\mathrm{1}\right)^{{n}−{k}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{e}^{{ikx}} \:{e}^{−{i}\left({n}−{k}\right){x}} {dx} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\left(−\mathrm{1}\right)^{{n}−{k}} \:{C}_{{n}} ^{{k}} \:\:.{A}_{{k}} \:\:\:{with}\:{A}_{{k}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{e}^{\left({ik}−{in}+{ik}\right){x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{e}^{{i}\left(\mathrm{2}{k}−{n}\right){x}} {dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{k}−{n}\right){x}\:{dx}\:+{i}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}\left(\mathrm{2}{k}−{n}\right){x}\:{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}{sin}\left(\mathrm{2}{k}−{n}\right){x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:+{i}\left[−\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}{cos}\left(\mathrm{2}{k}−{n}\right){x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}{sin}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\:+\frac{{i}}{\mathrm{2}{k}−{n}}\left(\:\mathrm{1}−{cos}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$${B}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{n}−{k}} \:{C}_{{n}} ^{{k}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−{n}}\left\{\:{sin}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\:+{i}\left(\mathrm{1}−{cos}\left(\mathrm{2}{k}−{n}\right)\frac{\pi}{\mathrm{4}}\right)\right\} \\ $$$$\:\Rightarrow{B}_{\mathrm{2}{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} \left(−\mathrm{1}\right)^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:\:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{2}{n}}\left\{{sin}\left({k}−{n}\right)\frac{\pi}{\mathrm{2}}\:+{i}\left(\mathrm{1}−{cos}\left({k}−{n}\right)\frac{\pi}{\mathrm{2}}\right)\right\} \\ $$$${but}\:{B}_{\mathrm{2}{n}} \:\:{is}\:{real}\:\Rightarrow\:{B}_{\mathrm{2}{n}} \:=\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:\:\:\frac{{sin}\left({k}−{n}\right)\frac{\pi}{\mathrm{2}}}{{k}−{n}}\: \\ $$$${and}\:{we}\:{follow}\:{the}\:{same}\:{method}\:{to}\:{find}\:{B}_{\mathrm{2}{n}+\mathrm{1}} \\ $$
Commented by maxmathsup by imad last updated on 25/Nov/18
![2) let I =∫_0 ^(π/4) cos^6 x dx and J =∫_0 ^(π/4) sin^6 x dx ⇒ I +J =∫_0 ^(π/4) { (cos^2 x)^(3 ) +(sin^2 x)^3 }dx =∫_0 ^(π/4) { (cos^2 x+sin^2 x)^3 −3cos^2 x sin^2 x(cos^2 x +sin^2 x)}dx =∫_0 ^(π/4) {1−3 cos^2 x sin^2 x}dx =∫_0 ^(π/4) {1−(3/4)(1+cos(2x))(1−cos(2x))dx =(π/4) −(3/4) ∫_0 ^(π/4) (1−cos^2 (2x))dx =(π/4) −(3/4).(π/4) +(3/4) ∫_0 ^(π/4) ((1+cos(4x))/2)dx =(π/(16)) +(3/8).(π/4) +(3/8) ∫_0 ^(π/4) cos(4x)dx =(π/(16)) +((3π)/(32)) +0 =((5π)/(32)) also we have I−J = ∫_0 ^(π/4) ( (cos^2 x)^3 −(sin^2 x)^3 dx =∫_0 ^(π/4) (cos^2 x −sin^2 x)(cos^4 x +cos^2 x sin^2 x +sin^4 x)dx =∫_0 ^(π/4) cos(2x)( (cos^2 x +sin^2 x)^2 −cos^2 x sin^2 x)dx =∫_0 ^(π/4) cos(2x)(1−(1/4)sin^2 (2x))dx=∫_0 ^(π/4) cos(2x)(1−(1/8)(1−cos(4x))dx =(7/8) ∫_0 ^(π/4) cos(2x)dx +(1/8) ∫_0 ^(π/4) cos(2x)cos(4x)dx but ∫_0 ^(π/4) cos(2x)dx =[(1/2)sin(2x)]_0 ^(π/4) =(1/2) ∫_0 ^(π/4) cos(2x)cos(4x) dx =(1/2) ∫_0 ^(π/4) (cos(6x)+cos(2x))dx =(1/(12))[sin(6x)]_0 ^(π/4) +(1/4)[sin(2x)]_0 ^(π/4) =(1/(12))sin(((3π)/2)) +(1/4) =−(1/(12)) +(1/4) =((−1+3)/(12)) =(1/6) ⇒ I −J =(7/(16)) +(1/(48)) =((22)/(48)) =((11)/(24)) ⇒ I +J =((5π)/(32)) and I −J =((11)/(24)) ⇒ 2I =((5π)/(32)) +((11)/(24)) ⇒ I =((5π)/(64)) +((11)/(48)) also 2J =((5π)/(32)) −((11)/(24)) ⇒ J =((5π)/(64)) −((11)/(48)) . J](Q48609.png)
$$\left.\mathrm{2}\right)\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{6}} {x}\:{dx}\:{and}\:{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{6}} {x}\:{dx}\:\Rightarrow \\ $$$${I}\:+{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\:\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}\:} \:+\left({sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \right\}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\:\left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\mathrm{3}{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\left({cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}\right)\right\}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\mathrm{1}−\mathrm{3}\:{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\right\}{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx}\right. \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{3}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{3}}{\mathrm{4}}.\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}{dx} \\ $$$$=\frac{\pi}{\mathrm{16}}\:\:+\frac{\mathrm{3}}{\mathrm{8}}.\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{4}{x}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{16}}\:+\frac{\mathrm{3}\pi}{\mathrm{32}}\:+\mathrm{0}\:=\frac{\mathrm{5}\pi}{\mathrm{32}}\:\:{also}\:{we}\:{have}\:{I}−{J}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\:\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\left({sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} {dx}\right. \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({cos}^{\mathrm{2}} {x}\:−{sin}^{\mathrm{2}} {x}\right)\left({cos}^{\mathrm{4}} {x}\:+{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{4}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}\left(\mathrm{2}{x}\right)\left(\:\left({cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)\right){dx}\right. \\ $$$$=\frac{\mathrm{7}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){dx}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right){dx}\:{but}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){dx}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right)\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left({cos}\left(\mathrm{6}{x}\right)+{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left[{sin}\left(\mathrm{6}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\frac{\mathrm{1}}{\mathrm{12}}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{12}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:=\frac{−\mathrm{1}+\mathrm{3}}{\mathrm{12}}\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow\:{I}\:−{J}\:=\frac{\mathrm{7}}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{48}}\:=\frac{\mathrm{22}}{\mathrm{48}}\:=\frac{\mathrm{11}}{\mathrm{24}}\:\Rightarrow\:{I}\:+{J}\:=\frac{\mathrm{5}\pi}{\mathrm{32}}\:{and}\:{I}\:−{J}\:=\frac{\mathrm{11}}{\mathrm{24}}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\frac{\mathrm{5}\pi}{\mathrm{32}}\:+\frac{\mathrm{11}}{\mathrm{24}}\:\Rightarrow\:{I}\:=\frac{\mathrm{5}\pi}{\mathrm{64}}\:+\frac{\mathrm{11}}{\mathrm{48}}\:{also}\:\:\mathrm{2}{J}\:=\frac{\mathrm{5}\pi}{\mathrm{32}}\:−\frac{\mathrm{11}}{\mathrm{24}}\:\Rightarrow\:{J}\:=\frac{\mathrm{5}\pi}{\mathrm{64}}\:−\frac{\mathrm{11}}{\mathrm{48}}\:. \\ $$$${J} \\ $$$$ \\ $$
Answered by Abdulhafeez Abu qatada last updated on 24/Nov/18
![If I_n = ∫sin^n x dx, I_n = ((−cosx.sin^(n−1) x)/n) + ((n−1)/n)I_(n−2) ∴ B_n = ∫_0 ^(π/4) sin^n x dx, B_n = [((−cosx.sin^(n−1) x)/n) + ((n−1)/n)A_(n−2) ]_0 ^(π/4) B_n = ((−(((√2)/2))^n )/n) + ((n−1)/n)B_(n−2) A_n = [((sinx.cos^(n−1) x)/n) + ((n−1)/n)A_(n−2) ]_0 ^(π/4) A_n = (((((√2)/2))^n )/n) + ((n−1)/n)A_(n−2) A_6 = (((((√2)/2))^6 )/6) + (5/6)A_4 A_6 = (((((√2)/2))^6 )/6) + (5/6)((((((√2)/2))^4 )/4) + (3/4)A_2 ) A_6 = (((((√2)/2))^6 )/6) + (5/6)((((((√2)/2))^4 )/4) ) + (5/6).(3/4)((((((√2)/2))^2 )/2) + (1/2)A_0 ) A_0 = ∫^(π/4) _0 dx = (π/4) A_6 = (((((√2)/2))^6 )/6) + (5/6)((((((√2)/2))^4 )/4) ) + (5/6).(3/4)((((((√2)/2))^2 )/2) + (π/8)) A_6 = ((5π)/(64)) + ((11)/(48)).....After simplifying B_6 = ((−(((√2)/2))^6 )/6) + (5/6)B_4 B_6 = ((−(((√2)/2))^6 )/6) + (5/6)(((−(((√2)/2))^4 )/4) + (3/4)B_2 ) B_6 = ((−(((√2)/2))^6 )/6) + (5/6)(((−(((√2)/2))^4 )/4) ) + (5/6).(3/4)(((−(((√2)/2))^2 )/2) + (1/2)B_0 ) B_0 = ∫^(π/4) _0 dx = (π/4) B_6 = ((−(((√2)/2))^6 )/6) + (5/6)(((−(((√2)/2))^4 )/4) ) + (5/6).(3/4)(((−(((√2)/2))^2 )/2) + (π/8)) B_6 = ((5π)/(64)) − ((11)/(48))......After simplifying Abu qatada](Q48512.png)
$$ \\ $$$$ \\ $$$${If}\:{I}_{{n}} \:=\:\int{sin}^{{n}} {x}\:{dx},\:{I}_{{n}} \:=\:\frac{−\mathrm{cos}{x}.\mathrm{sin}^{{n}−\mathrm{1}} {x}}{{n}}\:+\:\frac{{n}−\mathrm{1}}{{n}}{I}_{{n}−\mathrm{2}} \\ $$$$\therefore\:{B}_{{n}} \:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}{sin}^{{n}} {x}\:{dx},\:{B}_{{n}} \:=\:\left[\frac{−\mathrm{cos}{x}.\mathrm{sin}^{{n}−\mathrm{1}} {x}}{{n}}\:+\:\frac{{n}−\mathrm{1}}{{n}}{A}_{{n}−\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$${B}_{{n}} \:=\:\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{{n}} }{{n}}\:+\:\frac{{n}−\mathrm{1}}{{n}}{B}_{{n}−\mathrm{2}} \: \\ $$$$ \\ $$$${A}_{{n}} \:=\:\left[\frac{\mathrm{sin}{x}.\mathrm{cos}^{{n}−\mathrm{1}} {x}}{{n}}\:+\:\frac{{n}−\mathrm{1}}{{n}}{A}_{{n}−\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$${A}_{{n}} \:=\:\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{{n}} }{{n}}\:+\:\frac{{n}−\mathrm{1}}{{n}}{A}_{{n}−\mathrm{2}} \: \\ $$$${A}_{\mathrm{6}} \:=\:\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}{A}_{\mathrm{4}} \: \\ $$$${A}_{\mathrm{6}} \:=\:\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}{A}_{\mathrm{2}} \right) \\ $$$${A}_{\mathrm{6}} \:=\:\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}}\:\right)\:+\:\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{A}_{\mathrm{0}} \right) \\ $$$${A}_{\mathrm{0}} \:=\:\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{4}}} \:{dx}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$${A}_{\mathrm{6}} \:=\:\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}}\:\right)\:+\:\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\pi}{\mathrm{8}}\right) \\ $$$$ \\ $$$${A}_{\mathrm{6}} \:=\:\:\frac{\mathrm{5}\pi}{\mathrm{64}}\:+\:\frac{\mathrm{11}}{\mathrm{48}}.....{After}\:{simplifying} \\ $$$$ \\ $$$${B}_{\mathrm{6}} \:=\:\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}{B}_{\mathrm{4}} \: \\ $$$${B}_{\mathrm{6}} \:=\:\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}{B}_{\mathrm{2}} \right) \\ $$$${B}_{\mathrm{6}} \:=\:\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}}\:\right)\:+\:\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{B}_{\mathrm{0}} \right) \\ $$$$ \\ $$$${B}_{\mathrm{0}} \:=\:\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{4}}} \:{dx}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$$${B}_{\mathrm{6}} \:=\:\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{6}} }{\mathrm{6}}\:+\:\frac{\mathrm{5}}{\mathrm{6}}\left(\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}}\:\right)\:+\:\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\pi}{\mathrm{8}}\right) \\ $$$$ \\ $$$${B}_{\mathrm{6}} \:=\:\frac{\mathrm{5}\pi}{\mathrm{64}}\:−\:\frac{\mathrm{11}}{\mathrm{48}}......{After}\:{simplifying} \\ $$$$ \\ $$$${Abu}\:{qatada} \\ $$
Answered by Abdulhafeez Abu qatada last updated on 24/Nov/18
