
Question Number 48517 by ajfour last updated on 24/Nov/18

Commented by ajfour last updated on 25/Nov/18

$${Find}\:{ratio}\:{of}\:{maximum}\:{triangle} \\ $$$${area}\:\left({with}\:{A}\:{and}\:{B}\:{fixed}\right)\:{to} \\ $$$${ellipse}\:{area}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Nov/18
![A(a,0) B(0,−b) P(acosθ ,bsinθ) area (S)=(1/2)[x_1 (y_2 −y_3 )+x_2 (y_3 −y_1 )+x_3 (y_1 −y_2 )] =(1/2)[a(−b−bsinθ)+0(bsinθ−0)+acosθ(0+b)] =(1/2)[−ab−absinθ+abcosθ] =((−ab)/2)[1+sinθ−cosθ] =((−ab)/2)[1+(√2) ((1/(√2))sinθ−(1/(√2))cosθ)] =((−ab)/2)[1+(√2) sin(θ−(π/4))] max value of sin(θ−(π/4))=1 min value=−1 so S =((−ab)/2)[1+(√2) ] when sin(θ−(π/4))=1 S=((−ab)/2)[1−(√2) ]=((ab)/2)[(√2) −1] so max area=((ab)/2)[1+(√2) ] ( ofABP triangle) rewquired ratio=((((ab)/2)[1+(√2) ])/(πab))=((1+(√2) )/(2π))](Q48530.png)
$${A}\left({a},\mathrm{0}\right)\:\:{B}\left(\mathrm{0},−{b}\right)\:\:{P}\left({acos}\theta\:\:,{bsin}\theta\right) \\ $$$${area}\:\left({S}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}_{\mathrm{1}} \left({y}_{\mathrm{2}} −{y}_{\mathrm{3}} \right)+{x}_{\mathrm{2}} \left({y}_{\mathrm{3}} −{y}_{\mathrm{1}} \right)+{x}_{\mathrm{3}} \left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{a}\left(−{b}−{bsin}\theta\right)+\mathrm{0}\left({bsin}\theta−\mathrm{0}\right)+{acos}\theta\left(\mathrm{0}+{b}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−{ab}−{absin}\theta+{abcos}\theta\right] \\ $$$$=\frac{−{ab}}{\mathrm{2}}\left[\mathrm{1}+{sin}\theta−{cos}\theta\right] \\ $$$$=\frac{−{ab}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{sin}\theta−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{cos}\theta\right)\right] \\ $$$$=\frac{−{ab}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{2}}\:{sin}\left(\theta−\frac{\pi}{\mathrm{4}}\right)\right] \\ $$$${max}\:{value}\:{of}\:{sin}\left(\theta−\frac{\pi}{\mathrm{4}}\right)=\mathrm{1}\:\:\:{min}\:{value}=−\mathrm{1} \\ $$$${so}\:{S}\:=\frac{−{ab}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{2}}\:\right]\:{when}\:{sin}\left(\theta−\frac{\pi}{\mathrm{4}}\right)=\mathrm{1} \\ $$$${S}=\frac{−{ab}}{\mathrm{2}}\left[\mathrm{1}−\sqrt{\mathrm{2}}\:\right]=\frac{{ab}}{\mathrm{2}}\left[\sqrt{\mathrm{2}}\:−\mathrm{1}\right] \\ $$$${so}\:{max}\:{area}=\frac{{ab}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{2}}\:\right]\:\:\left(\:{ofABP}\:{triangle}\right) \\ $$$$ \\ $$$${rewquired}\:{ratio}=\frac{\frac{{ab}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{2}}\:\right]}{\pi{ab}}=\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:}{\mathrm{2}\pi} \\ $$
Commented by ajfour last updated on 25/Nov/18
$${Thanks}\:{Sir},\:{i}'{d}\:{got}\:{the}\:{same}\:{ans}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Nov/18

$${thank}\:{you}\:{sir}... \\ $$
Answered by ajfour last updated on 25/Nov/18

$${Area}\:{of}\:\bigtriangleup{APB}\:{is}\:{maximum} \\ $$$${when}\:{P}\:{is}\:{farthest}\:{from}\:{base} \\ $$$${AB}. \\ $$$$\Rightarrow\:\:{P}\:{is}\:{contact}\:{point}\:{of}\:{a}\:{tangent} \\ $$$${to}\:{ellipse}\:{that}\:{is}\:{parallel}\:{to}\:{AB}. \\ $$$${let}\:{P}\:\left({h},{k}\right). \\ $$$${eq}.\:{of}\:{ellipse}:\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}\:=\:−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{h}}{{k}}\right)\:=\:{slope}\:{of}\:{AB}\:=\:\frac{{b}}{{a}} \\ $$$$\Rightarrow\:\frac{{h}}{{k}}\:=\:−\frac{{a}}{{b}}\:\:\:\&\:\:\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }×\frac{{k}^{\mathrm{2}} }{{h}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:=\:\mathrm{1}\:\: \\ $$$$\Rightarrow\:\:\left({h},{k}\right)\equiv\:\left(−\frac{{a}}{\sqrt{\mathrm{2}}},\:\frac{{b}}{\sqrt{\mathrm{2}}}\right) \\ $$$$\bot\:{distance}\:{of}\:{P}\:{from}\:{line}\:{AB}\:{is} \\ $$$$\:\:\:\:\:{p}\:=\:\frac{\mid\frac{−{a}/\sqrt{\mathrm{2}}}{{a}}−\frac{{b}/\sqrt{\mathrm{2}}}{{b}}−\mathrm{1}\mid}{\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }}}\:=\:\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${maximum}\:{area}\:{of}\:\bigtriangleup{APB}\:{is} \\ $$$$\:\:\:\:\bigtriangleup\:=\:\frac{{p}}{\mathrm{2}}×\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:=\:\frac{{ab}}{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\frac{{max}.\:{area}\:{of}\:\bigtriangleup{APB}}{{area}\:{of}\:{ellipse}}\:=\:\frac{\frac{{ab}}{\mathrm{2}}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}{\pi{ab}} \\ $$$$\:\:\:\:=\:\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{2}\pi}\:. \\ $$$$ \\ $$
Answered by mr W last updated on 25/Nov/18
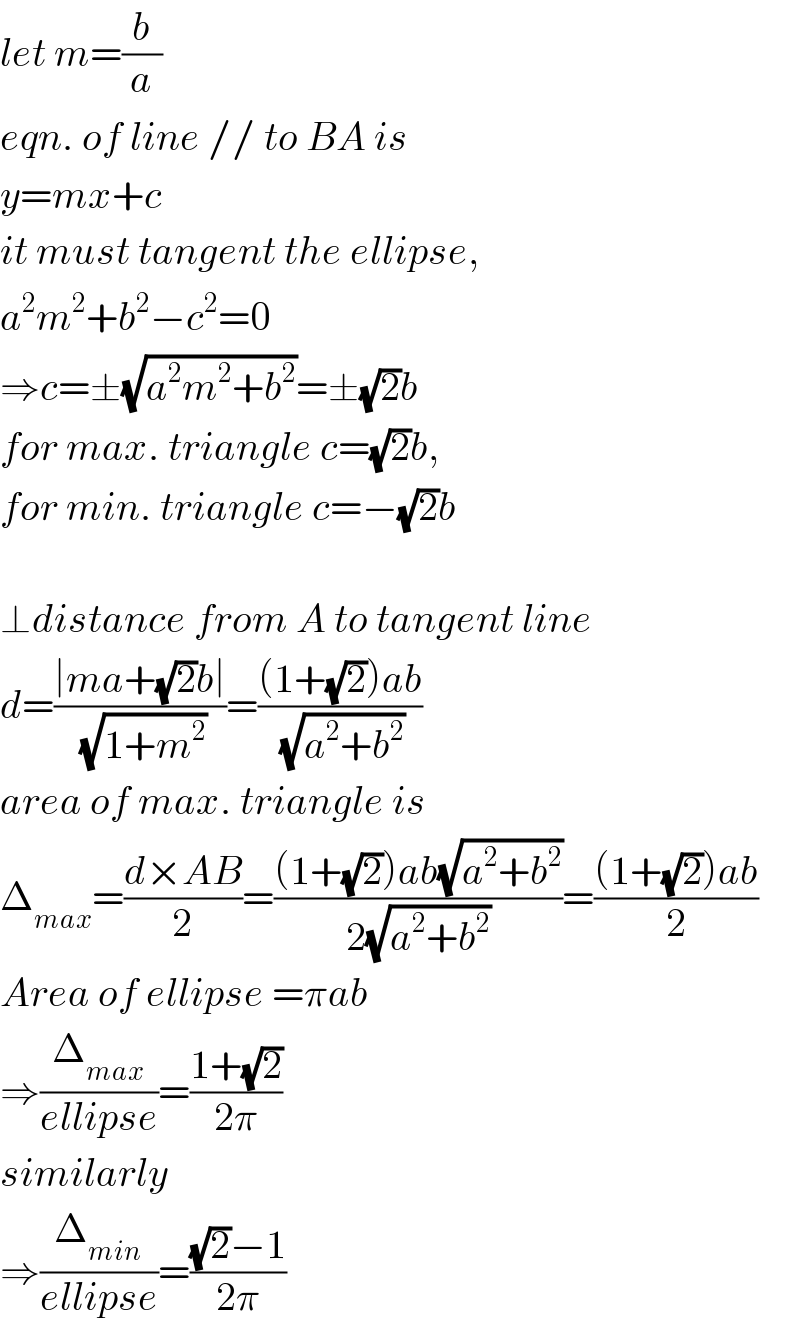
$${let}\:{m}=\frac{{b}}{{a}} \\ $$$${eqn}.\:{of}\:{line}\://\:{to}\:{BA}\:{is} \\ $$$${y}={mx}+{c} \\ $$$${it}\:{must}\:{tangent}\:{the}\:{ellipse}, \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{c}=\pm\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\pm\sqrt{\mathrm{2}}{b} \\ $$$${for}\:{max}.\:{triangle}\:{c}=\sqrt{\mathrm{2}}{b}, \\ $$$${for}\:{min}.\:{triangle}\:{c}=−\sqrt{\mathrm{2}}{b} \\ $$$$ \\ $$$$\bot{distance}\:{from}\:{A}\:{to}\:{tangent}\:{line} \\ $$$${d}=\frac{\mid{ma}+\sqrt{\mathrm{2}}{b}\mid}{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){ab}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${area}\:{of}\:{max}.\:{triangle}\:{is} \\ $$$$\Delta_{{max}} =\frac{{d}×{AB}}{\mathrm{2}}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){ab}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){ab}}{\mathrm{2}} \\ $$$${Area}\:{of}\:{ellipse}\:=\pi{ab} \\ $$$$\Rightarrow\frac{\Delta_{{max}} }{{ellipse}}=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}\pi} \\ $$$${similarly} \\ $$$$\Rightarrow\frac{\Delta_{{min}} }{{ellipse}}=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}\pi} \\ $$
