Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 48638 by mr W last updated on 26/Nov/18

Commented by mr W last updated on 26/Nov/18

Find the locus of P such that PO is the bisector of ∠APB.

$${Find}\:{the}\:{locus}\:{of}\:{P}\:{such}\:{that}\:{PO} \\ $$$${is}\:{the}\:{bisector}\:{of}\:\angle{APB}. \\ $$

Commented by ajfour last updated on 28/Nov/18

Commented by ajfour last updated on 28/Nov/18

(a/(sin φ)) = (r/(sin (θ+φ))) & (b/(sin φ)) = (r/(sin ((π/2)−θ+φ))) = (r/(cos (θ−φ))) ⇒ sin θcos φ+cos θsin φ=(r/a)sin φ sin θsin φ+cos θcos φ+=(r/b)sin φ ⇒ sin θ = ((rsin φ(((cos φ)/a)−((sin φ)/b)))/(cos^2 φ−sin^2 φ)) cos θ = ((rsin φ(((cos φ)/b)−((sin φ)/a)))/(cos^2 φ−sin^2 φ)) ⇒ 1=((r^2 sin^2 φ[(((cos φ)/a)−((sin φ)/b))^2 +(((cos φ)/b)−((sin φ)/a))^2 ])/((cos^2 φ−sin^2 φ)^2 )) ⇒ 1=((r^2 sin^2 φ[(1/a^2 )+(1/b^2 )−((4sin φcos φ)/(ab))])/((cos^2 φ−sin^2 φ)^2 )) ⇒ r^2 = ((cos^2 2φ)/(sin^2 φ((1/a^2 )+(1/b^2 )−((2sin 2φ)/(ab))))) r^2 = ((cot^2 φ−1)/((1/a^2 )+(1/b^2 )−((2sin 2φ)/(ab)))) ((2rdr)/dφ) = 0 ⇒ −2cot φcosec^2 φ((1/a^2 )+(1/b^2 )−((2sin 2φ)/(ab))) = ((−4cos 2φ)/(ab))(cot^2 φ−1) ⇒ ((a^2 +b^2 )/(2ab))−sin 2φ = cos^2 2φtan φ let tan φ = t , ((a^2 +b^2 )/(2ab)) = c ⇒ t(((1−t^2 )/(1+t^2 )))^2 +((2t)/(1+t^2 ))−c = 0 ⇒ t(1−t^2 )^2 +2t(1+t^2 )−c(1+t^2 )^2 = 0 .....

$$\frac{{a}}{\mathrm{sin}\:\phi}\:=\:\frac{{r}}{\mathrm{sin}\:\left(\theta+\phi\right)}\:\:\:\& \\ $$$$\frac{{b}}{\mathrm{sin}\:\phi}\:=\:\frac{{r}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta+\phi\right)}\:=\:\frac{{r}}{\mathrm{cos}\:\left(\theta−\phi\right)} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\mathrm{cos}\:\phi+\mathrm{cos}\:\theta\mathrm{sin}\:\phi=\left({r}/{a}\right)\mathrm{sin}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\mathrm{sin}\:\theta\mathrm{sin}\:\phi+\mathrm{cos}\:\theta\mathrm{cos}\:\phi+=\left({r}/{b}\right)\mathrm{sin}\:\phi \\ $$$$\Rightarrow\:\mathrm{sin}\:\theta\:=\:\frac{{r}\mathrm{sin}\:\phi\left(\frac{\mathrm{cos}\:\phi}{{a}}−\frac{\mathrm{sin}\:\phi}{{b}}\right)}{\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi} \\ $$$$\:\:\:\:\mathrm{cos}\:\theta\:=\:\frac{{r}\mathrm{sin}\:\phi\left(\frac{\mathrm{cos}\:\phi}{{b}}−\frac{\mathrm{sin}\:\phi}{{a}}\right)}{\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi} \\ $$$$\Rightarrow\:\mathrm{1}=\frac{{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi\left[\left(\frac{\mathrm{cos}\:\phi}{{a}}−\frac{\mathrm{sin}\:\phi}{{b}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{cos}\:\phi}{{b}}−\frac{\mathrm{sin}\:\phi}{{a}}\right)^{\mathrm{2}} \right]}{\left(\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{1}=\frac{{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi\left[\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{4sin}\:\phi\mathrm{cos}\:\phi}{{ab}}\right]}{\left(\mathrm{cos}\:^{\mathrm{2}} \phi−\mathrm{sin}\:^{\mathrm{2}} \phi\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} \:=\:\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\phi}{\mathrm{sin}\:^{\mathrm{2}} \phi\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{2sin}\:\mathrm{2}\phi}{{ab}}\right)} \\ $$$$\:\:\:\:\:\:{r}^{\mathrm{2}} \:=\:\frac{\mathrm{cot}\:^{\mathrm{2}} \phi−\mathrm{1}}{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{2sin}\:\mathrm{2}\phi}{{ab}}} \\ $$$$\:\frac{\mathrm{2}{rdr}}{{d}\phi}\:=\:\mathrm{0}\:\Rightarrow \\ $$$$−\mathrm{2cot}\:\phi\mathrm{cosec}\:^{\mathrm{2}} \phi\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{2sin}\:\mathrm{2}\phi}{{ab}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{4cos}\:\mathrm{2}\phi}{{ab}}\left(\mathrm{cot}\:^{\mathrm{2}} \phi−\mathrm{1}\right) \\ $$$$\Rightarrow\:\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}{ab}}−\mathrm{sin}\:\mathrm{2}\phi\:=\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\phi\mathrm{tan}\:\phi \\ $$$${let}\:\:\:\:\mathrm{tan}\:\phi\:=\:{t}\:,\:\:\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}{ab}}\:=\:\boldsymbol{{c}} \\ $$$$\Rightarrow\:\:{t}\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−{c}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−{c}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$$..... \\ $$

Commented by mr W last updated on 28/Nov/18

thanks sir! we can also build the eqn. w.r.t. θ: (r/a)=cos θ+sin θ (((b/a) tan θ−1)/(tan θ−(b/a))) MJS sir has solved the maximum for this eqn. in Q48739.

$${thanks}\:{sir}! \\ $$$${we}\:{can}\:{also}\:{build}\:{the}\:{eqn}.\:{w}.{r}.{t}.\:\theta: \\ $$$$\frac{{r}}{{a}}=\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\frac{\frac{{b}}{{a}}\:\mathrm{tan}\:\theta−\mathrm{1}}{\mathrm{tan}\:\theta−\frac{{b}}{{a}}} \\ $$$${MJS}\:{sir}\:{has}\:{solved}\:{the}\:{maximum}\:{for} \\ $$$${this}\:{eqn}.\:{in}\:{Q}\mathrm{48739}. \\ $$

Answered by ajfour last updated on 26/Nov/18

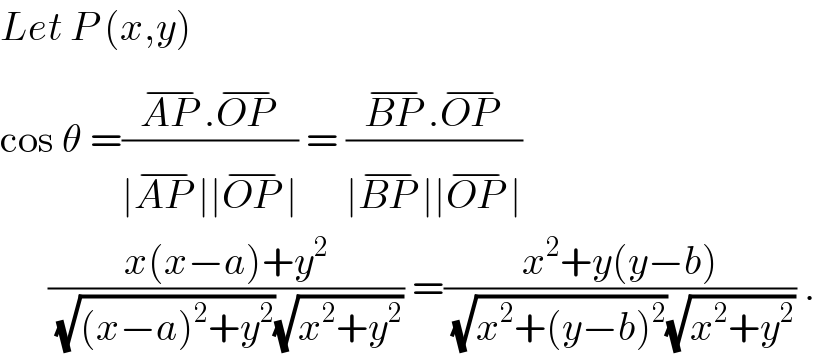
Let P (x,y) cos θ =((AP ^(−) .OP ^(−) )/(∣AP ^(−) ∣∣OP ^(−) ∣)) = ((BP ^(−) .OP ^(−) )/(∣BP ^(−) ∣∣OP ^(−) ∣)) ((x(x−a)+y^2 )/((√((x−a)^2 +y^2 ))(√(x^2 +y^2 )))) =((x^2 +y(y−b))/((√(x^2 +(y−b)^2 ))(√(x^2 +y^2 )))) .

$${Let}\:{P}\:\left({x},{y}\right) \\ $$$$\mathrm{cos}\:\theta\:=\frac{\overline {{AP}\:}.\overline {{OP}\:}}{\mid\overline {{AP}\:}\mid\mid\overline {{OP}\:}\mid}\:=\:\frac{\overline {{BP}\:}.\overline {{OP}\:}}{\mid\overline {{BP}\:}\mid\mid\overline {{OP}\:}\mid} \\ $$$$\:\:\:\:\:\:\frac{{x}\left({x}−{a}\right)+{y}^{\mathrm{2}} }{\sqrt{\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:=\frac{{x}^{\mathrm{2}} +{y}\left({y}−{b}\right)}{\sqrt{{x}^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} }\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:. \\ $$

Commented by ajfour last updated on 26/Nov/18

should not be omitted, it might serve to remind that origin cannot be a point of locus (for θ is not deined then).

$${should}\:{not}\:{be}\:{omitted},\:{it}\:{might} \\ $$$${serve}\:{to}\:{remind}\:{that}\:{origin}\:{cannot} \\ $$$${be}\:{a}\:{point}\:{of}\:{locus}\:\left({for}\:\theta\:{is}\:{not}\right. \\ $$$$\left.{deined}\:{then}\right). \\ $$

Commented by mr W last updated on 26/Nov/18

Ok sir! assume P is only in first quadrant. let R=OP is there a max. R?

$${Ok}\:{sir}! \\ $$$${assume}\:{P}\:{is}\:{only}\:{in}\:{first}\:{quadrant}. \\ $$$${let}\:{R}={OP} \\ $$$${is}\:{there}\:{a}\:{max}.\:{R}?\: \\ $$

Commented by ajfour last updated on 26/Nov/18

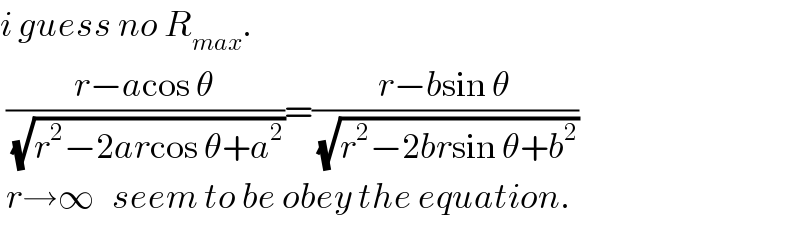
i guess no R_(max) . ((r−acos θ)/(√(r^2 −2arcos θ+a^2 )))=((r−bsin θ)/(√(r^2 −2brsin θ+b^2 ))) r→∞ seem to be obey the equation.

$${i}\:{guess}\:{no}\:{R}_{{max}} . \\ $$$$\:\frac{{r}−{a}\mathrm{cos}\:\theta}{\sqrt{{r}^{\mathrm{2}} −\mathrm{2}{ar}\mathrm{cos}\:\theta+{a}^{\mathrm{2}} }}=\frac{{r}−{b}\mathrm{sin}\:\theta}{\sqrt{{r}^{\mathrm{2}} −\mathrm{2}{br}\mathrm{sin}\:\theta+{b}^{\mathrm{2}} }} \\ $$$$\:{r}\rightarrow\infty\:\:\:{seem}\:{to}\:{be}\:{obey}\:{the}\:{equation}. \\ $$

Commented by mr W last updated on 26/Nov/18

thank you sir! ∣OP∣ on both sides can be omitted. so the eqn. is ((x^2 +y^2 −ax)/(√((x−a)^2 +y^2 ))) =((x^2 +y^2 −by)/(√(x^2 +(y−b)^2 ))) I′m trying to image how it looks like.

$${thank}\:{you}\:{sir}! \\ $$$$\mid{OP}\mid\:{on}\:{both}\:{sides}\:{can}\:{be}\:{omitted}.\:{so} \\ $$$${the}\:{eqn}.\:{is} \\ $$$$\:\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{ax}}{\sqrt{\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:=\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{by}}{\sqrt{{x}^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} }} \\ $$$${I}'{m}\:{trying}\:{to}\:{image}\:{how}\:{it}\:{looks}\:{like}. \\ $$

Commented by mr W last updated on 27/Nov/18

Commented by mr W last updated on 27/Nov/18

for the case a>b, the locus of poini P in the first quadrant is the red curve. we have point P_1 with distance R_1 to the origin. we have point P_2 =A with distance R_2 to the origin (R_2 =a). we can see 0<r≤R_1 and R_2 <r<∞. that means for R_1 <r<R_2 there is no solution for θ. R_1 is a kind of local maximum for r.

$${for}\:{the}\:{case}\:{a}>{b},\:{the}\:{locus}\:{of}\:{poini}\:{P} \\ $$$${in}\:{the}\:{first}\:{quadrant}\:{is}\:{the}\:{red}\:{curve}. \\ $$$${we}\:{have}\:{point}\:{P}_{\mathrm{1}} \:{with}\:{distance}\:{R}_{\mathrm{1}} \:{to} \\ $$$${the}\:{origin}.\:{we}\:{have}\:{point}\:{P}_{\mathrm{2}} \:={A}\:{with} \\ $$$${distance}\:{R}_{\mathrm{2}} \:{to}\:{the}\:{origin}\:\left({R}_{\mathrm{2}} ={a}\right). \\ $$$${we}\:{can}\:{see}\:\mathrm{0}<{r}\leqslant{R}_{\mathrm{1}} \:{and}\:{R}_{\mathrm{2}} <{r}<\infty. \\ $$$${that}\:{means}\:{for}\:{R}_{\mathrm{1}} <{r}<{R}_{\mathrm{2}} \:{there}\:{is} \\ $$$${no}\:{solution}\:{for}\:\theta.\:{R}_{\mathrm{1}} \:{is}\:{a}\:{kind}\:{of}\:{local} \\ $$$${maximum}\:{for}\:{r}. \\ $$

Commented by mr W last updated on 27/Nov/18

Commented by mr W last updated on 27/Nov/18

this diagram shows the case a=4, b=3. for r in the shaded area there is no solution. since r is the length of the rod, that means we can not find a solution for some lengthes of rod.

$${this}\:{diagram}\:{shows}\:{the}\:{case}\:{a}=\mathrm{4},\:{b}=\mathrm{3}. \\ $$$${for}\:{r}\:{in}\:{the}\:{shaded}\:{area}\:{there}\:{is}\:{no} \\ $$$${solution}.\:{since}\:{r}\:{is}\:{the}\:{length}\:{of}\:{the} \\ $$$${rod},\:{that}\:{means}\:{we}\:{can}\:{not}\:{find}\:{a} \\ $$$${solution}\:{for}\:{some}\:{lengthes}\:{of}\:{rod}. \\ $$

Commented by ajfour last updated on 27/Nov/18

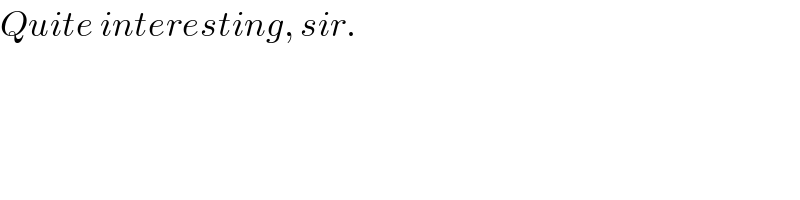
Quite interesting, sir.

$${Quite}\:{interesting},\:{sir}. \\ $$

Commented by mr W last updated on 27/Nov/18

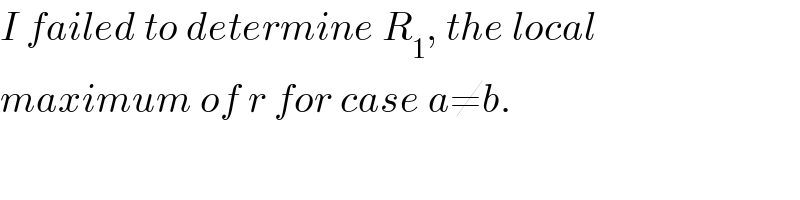
I failed to determine R_1 , the local maximum of r for case a≠b.

$${I}\:{failed}\:{to}\:{determine}\:{R}_{\mathrm{1}} ,\:{the}\:{local} \\ $$$${maximum}\:{of}\:{r}\:{for}\:{case}\:{a}\neq{b}. \\ $$

Commented by ajfour last updated on 28/Nov/18

i am not in good health sir.

$${i}\:{am}\:{not}\:{in}\:{good}\:{health}\:{sir}. \\ $$

Commented by mr W last updated on 28/Nov/18

sorry to hear this sir. I wish you a full recovery a.s.a.p.!

$${sorry}\:{to}\:{hear}\:{this}\:{sir}.\:{I}\:{wish}\:{you}\:{a}\:{full} \\ $$$${recovery}\:{a}.{s}.{a}.{p}.! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com