
Question and Answers Forum
Question Number 48667 by maxmathsup by imad last updated on 26/Nov/18
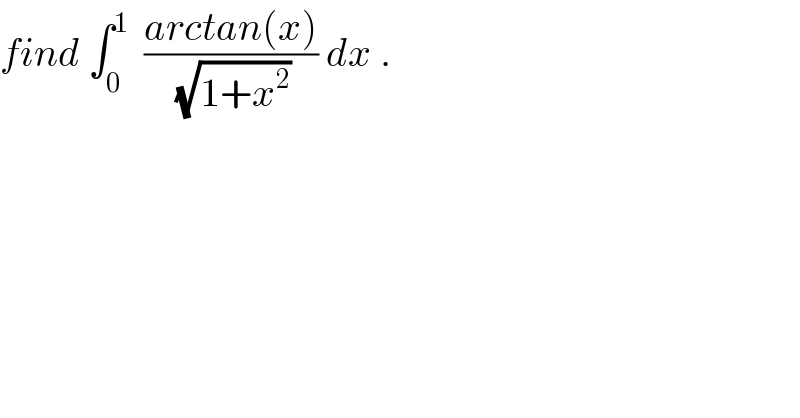
Commented by Abdo msup. last updated on 02/Dec/18
![changement x=tant give I =∫_0 ^(π/4) (t/(√(1+tan^2 t))) (1+tan^2 t)dt =∫_0 ^(π/4) t (dt/(cost)) =∫_0 ^(π/4) (t/(cost)) dt =_(tan((t/2))=u) ∫_0 ^((√2)−1) ((2arctanu)/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) =4 ∫_0 ^((√2)−1) ((arctan(u))/(1−u^2 )) du =4 ∫_0 ^((√2)−1) arctan(u)(Σ_(n=0) ^∞ u^(2n) )du =4 Σ_(n=0) ^∞ ∫_0 ^((√2)−1) u^(2n) arctan u du =4 Σ_(n=0) ^∞ A_n by parts A_n =∫_0 ^((√2)−1) u^(2n) arctan(u)du =[(1/(2n+1))u^(2n+1) arctanu]_0 ^((√2) −1) +∫_0 ^((√2)−1) (1/(2n+1)) u^(2n+1) (du/(1+u^2 )) =(1/(2n+1))((√2)−1)^(2n+1) arctan((√2)−1) +(1/(2n+1))∫_0 ^((√2)−1) (u^(2n+1) /(1+u^2 ))du =((π((√2)−1)^(2n+1) )/(8(2n+1))) +(1/(2n+1)) ∫_0 ^((√2)−1) (u^(2n+1) /(1+u^2 )) du but ∫_0 ^((√2)−1) (u^(2n+1) /(1+u^2 )) du =_(tanθ=u) ∫_0 ^(π/8) ((tan^(2n+1) θ)/(1+tan^2 θ)) (1+tan^2 θ)dθ = ∫_0 ^(π/8) tan^(2n+1) θ dθ ....be continued....](Q49110.png)
Answered by Abdulhafeez Abu qatada last updated on 26/Nov/18

| ||
Question and Answers Forum | ||
Question Number 48667 by maxmathsup by imad last updated on 26/Nov/18 | ||
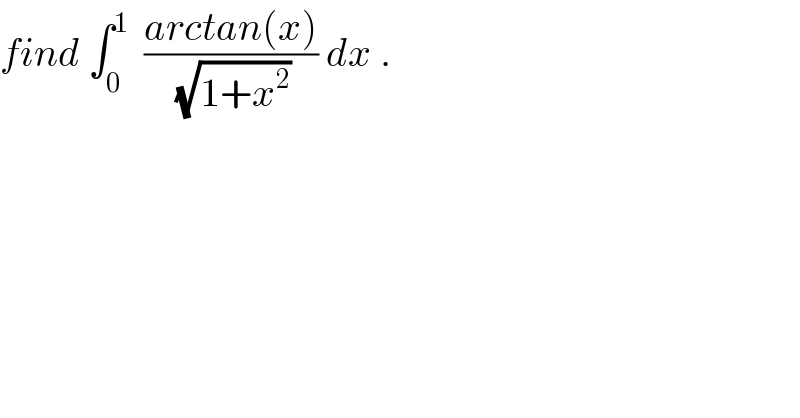 | ||
Commented by Abdo msup. last updated on 02/Dec/18 | ||
![changement x=tant give I =∫_0 ^(π/4) (t/(√(1+tan^2 t))) (1+tan^2 t)dt =∫_0 ^(π/4) t (dt/(cost)) =∫_0 ^(π/4) (t/(cost)) dt =_(tan((t/2))=u) ∫_0 ^((√2)−1) ((2arctanu)/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) =4 ∫_0 ^((√2)−1) ((arctan(u))/(1−u^2 )) du =4 ∫_0 ^((√2)−1) arctan(u)(Σ_(n=0) ^∞ u^(2n) )du =4 Σ_(n=0) ^∞ ∫_0 ^((√2)−1) u^(2n) arctan u du =4 Σ_(n=0) ^∞ A_n by parts A_n =∫_0 ^((√2)−1) u^(2n) arctan(u)du =[(1/(2n+1))u^(2n+1) arctanu]_0 ^((√2) −1) +∫_0 ^((√2)−1) (1/(2n+1)) u^(2n+1) (du/(1+u^2 )) =(1/(2n+1))((√2)−1)^(2n+1) arctan((√2)−1) +(1/(2n+1))∫_0 ^((√2)−1) (u^(2n+1) /(1+u^2 ))du =((π((√2)−1)^(2n+1) )/(8(2n+1))) +(1/(2n+1)) ∫_0 ^((√2)−1) (u^(2n+1) /(1+u^2 )) du but ∫_0 ^((√2)−1) (u^(2n+1) /(1+u^2 )) du =_(tanθ=u) ∫_0 ^(π/8) ((tan^(2n+1) θ)/(1+tan^2 θ)) (1+tan^2 θ)dθ = ∫_0 ^(π/8) tan^(2n+1) θ dθ ....be continued....](Q49110.png) | ||
Answered by Abdulhafeez Abu qatada last updated on 26/Nov/18 | ||
 | ||