Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 48715 by Abdo msup. last updated on 27/Nov/18

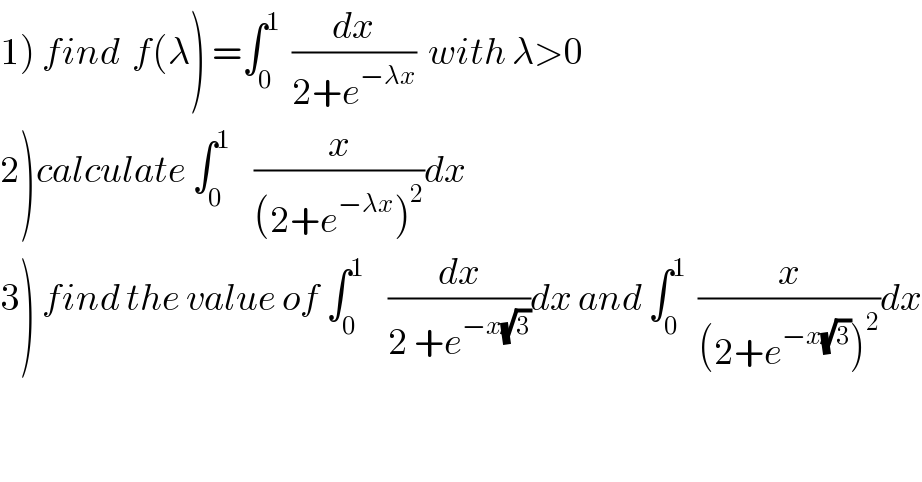
1) find f(λ) =∫_0 ^1 (dx/(2+e^(−λx) )) with λ>0 2)calculate ∫_0 ^1 (x/((2+e^(−λx) )^2 ))dx 3) find the value of ∫_0 ^1 (dx/(2 +e^(−x(√3)) ))dx and ∫_0 ^1 (x/((2+e^(−x(√3)) )^2 ))dx

$$\left.\mathrm{1}\right)\:{find}\:\:{f}\left(\lambda\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{2}+{e}^{−\lambda{x}} }\:\:{with}\:\lambda>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}}{\left(\mathrm{2}+{e}^{−\lambda{x}} \right)^{\mathrm{2}} }{dx} \\ $$ $$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\mathrm{2}\:+{e}^{−{x}\sqrt{\mathrm{3}}} }{dx}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\left(\mathrm{2}+{e}^{−{x}\sqrt{\mathrm{3}}} \right)^{\mathrm{2}} }{dx} \\ $$

Commented bymaxmathsup by imad last updated on 01/Dec/18

1) we have f(λ)=∫_0 ^1 (dx/(2+e^(−λx) )) changement e^(λx ) =t give λx=ln(t) ⇒ x=(1/λ)ln(t) ⇒f(λ)=∫_1 ^e^λ (1/(λ(2+t^(−1) ))) (dt/t) =(1/λ) ∫_1 ^e^λ (dt/(2t +1)) =(1/(2λ))[ln(2t+1)]_1 ^e^λ = (1/(2λ)){ln(2e^λ +1)−ln(3)} ⇒ f(λ)=(1/(2λ)){ln(2 e^λ +1)−ln(3)} .

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left(\lambda\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{2}+{e}^{−\lambda{x}} }\:\:{changement}\:\:{e}^{\lambda{x}\:} ={t}\:{give}\:\lambda{x}={ln}\left({t}\right)\:\Rightarrow \\ $$ $${x}=\frac{\mathrm{1}}{\lambda}{ln}\left({t}\right)\:\Rightarrow{f}\left(\lambda\right)=\int_{\mathrm{1}} ^{{e}^{\lambda} } \:\:\:\:\:\frac{\mathrm{1}}{\lambda\left(\mathrm{2}+{t}^{−\mathrm{1}} \right)}\:\frac{{dt}}{{t}}\:=\frac{\mathrm{1}}{\lambda}\:\int_{\mathrm{1}} ^{{e}^{\lambda} } \:\:\:\frac{{dt}}{\mathrm{2}{t}\:+\mathrm{1}} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}\lambda}\left[{ln}\left(\mathrm{2}{t}+\mathrm{1}\right)\right]_{\mathrm{1}} ^{{e}^{\lambda} } \:\:=\:\frac{\mathrm{1}}{\mathrm{2}\lambda}\left\{{ln}\left(\mathrm{2}{e}^{\lambda} \:+\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\right\}\:\:\:\Rightarrow \\ $$ $${f}\left(\lambda\right)=\frac{\mathrm{1}}{\mathrm{2}\lambda}\left\{{ln}\left(\mathrm{2}\:{e}^{\lambda} \:+\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\right\}\:. \\ $$

Commented bymaxmathsup by imad last updated on 01/Dec/18

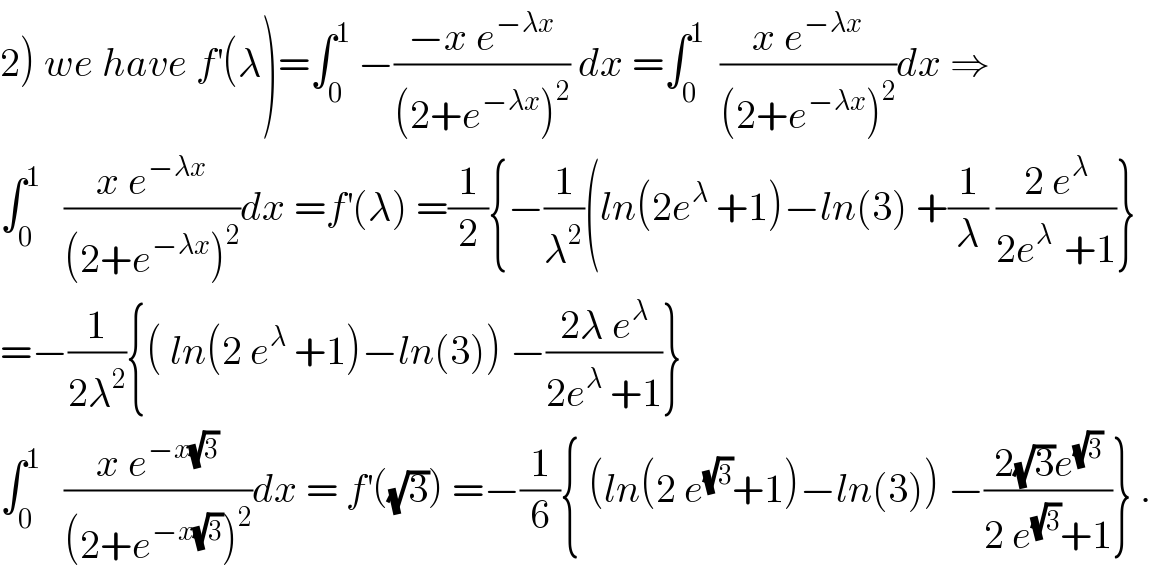
2) we have f^′ (λ)=∫_0 ^1 −((−x e^(−λx) )/((2+e^(−λx) )^2 )) dx =∫_0 ^1 ((x e^(−λx) )/((2+e^(−λx) )^2 ))dx ⇒ ∫_0 ^1 ((x e^(−λx) )/((2+e^(−λx) )^2 ))dx =f^′ (λ) =(1/2){−(1/λ^2 )(ln(2e^λ +1)−ln(3) +(1/λ) ((2 e^λ )/(2e^(λ ) +1))} =−(1/(2λ^2 )){( ln(2 e^λ +1)−ln(3)) −((2λ e^λ )/(2e^λ +1))} ∫_0 ^1 ((x e^(−x(√3)) )/((2+e^(−x(√3)) )^2 ))dx = f^′ ((√3)) =−(1/6){ (ln(2 e^(√3) +1)−ln(3)) −((2(√3)e^(√3) )/(2 e^(√3) +1))} .

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left(\lambda\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{−{x}\:{e}^{−\lambda{x}} }{\left(\mathrm{2}+{e}^{−\lambda{x}} \right)^{\mathrm{2}} }\:{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}\:{e}^{−\lambda{x}} }{\left(\mathrm{2}+{e}^{−\lambda{x}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}\:{e}^{−\lambda{x}} }{\left(\mathrm{2}+{e}^{−\lambda{x}} \right)^{\mathrm{2}} }{dx}\:={f}^{'} \left(\lambda\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }\left({ln}\left(\mathrm{2}{e}^{\lambda} \:+\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\:+\frac{\mathrm{1}}{\lambda}\:\frac{\mathrm{2}\:{e}^{\lambda} }{\mathrm{2}{e}^{\lambda\:} \:+\mathrm{1}}\right\}\right. \\ $$ $$=−\frac{\mathrm{1}}{\mathrm{2}\lambda^{\mathrm{2}} }\left\{\left(\:{ln}\left(\mathrm{2}\:{e}^{\lambda} \:+\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\right)\:−\frac{\mathrm{2}\lambda\:{e}^{\lambda} }{\mathrm{2}{e}^{\lambda} \:+\mathrm{1}}\right\} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}\:{e}^{−{x}\sqrt{\mathrm{3}}} }{\left(\mathrm{2}+{e}^{−{x}\sqrt{\mathrm{3}}} \right)^{\mathrm{2}} }{dx}\:=\:{f}^{'} \left(\sqrt{\mathrm{3}}\right)\:=−\frac{\mathrm{1}}{\mathrm{6}}\left\{\:\left({ln}\left(\mathrm{2}\:{e}^{\sqrt{\mathrm{3}}} +\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\right)\:−\frac{\mathrm{2}\sqrt{\mathrm{3}}{e}^{\sqrt{\mathrm{3}}} }{\mathrm{2}\:{e}^{\sqrt{\mathrm{3}}} +\mathrm{1}}\right\}\:. \\ $$

Commented bymaxmathsup by imad last updated on 01/Dec/18

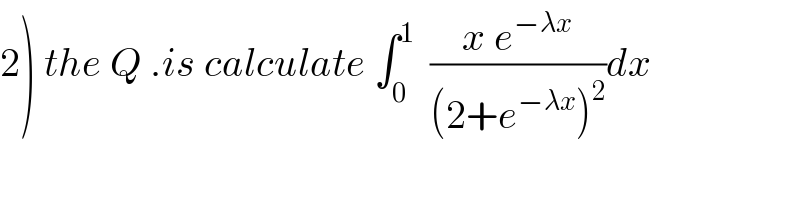
2) the Q .is calculate ∫_0 ^1 ((x e^(−λx) )/((2+e^(−λx) )^2 ))dx

$$\left.\mathrm{2}\right)\:{the}\:{Q}\:.{is}\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}\:{e}^{−\lambda{x}} }{\left(\mathrm{2}+{e}^{−\lambda{x}} \right)^{\mathrm{2}} }{dx} \\ $$

Commented bymaxmathsup by imad last updated on 01/Dec/18

) we have ∫_0 ^1 (dx/(2+e^(−x(√3)) )) =f((√3)) =(1/(2(√3))){ln(2 e^(√3) +1)−ln(3)}

$$\left.\right)\:{we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{2}+{e}^{−{x}\sqrt{\mathrm{3}}} }\:={f}\left(\sqrt{\mathrm{3}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left\{{ln}\left(\mathrm{2}\:{e}^{\sqrt{\mathrm{3}}} +\mathrm{1}\right)−{ln}\left(\mathrm{3}\right)\right\}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com