∫ ∫ (√(x^2 + y^2 )) dx dy, (√(3y)) ≤ x ≤ (√(4 − y^2 )) , 0 ≤ y ≤ 2


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 48725 by Tawa1 last updated on 27/Nov/18

$\int \int \sqrt{x^{2} + y^{2}} dx dy, \sqrt{3 y} ⩽ x ⩽ \sqrt{4 - y^{2}}, 0 ⩽ y ⩽ 2$
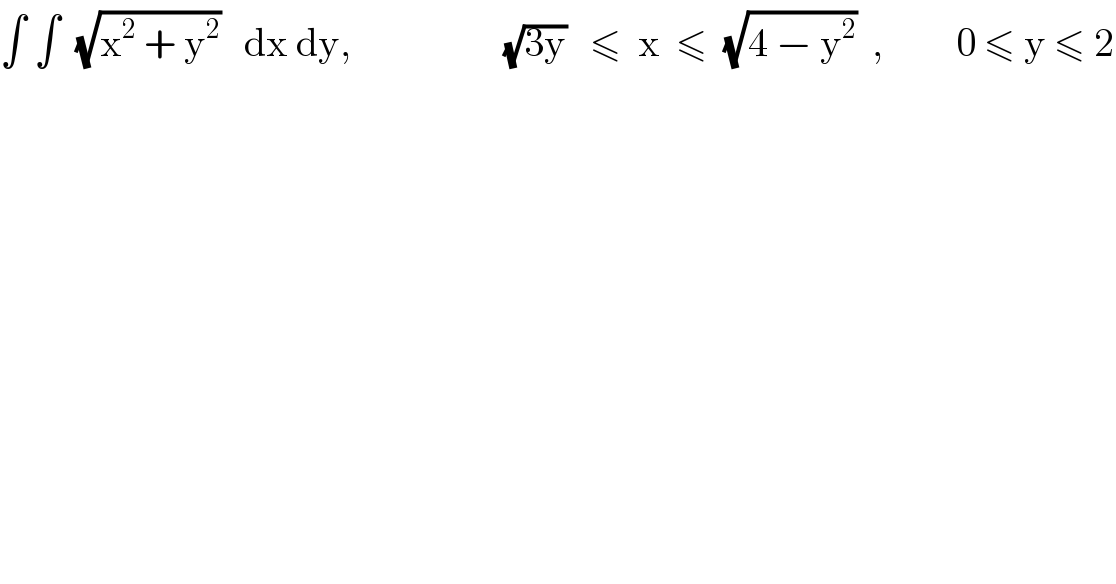
Commented by Abdo msup. last updated on 27/Nov/18
$let I =∫∫_D (√(x^2 +y^2 ))dxdy with D={(x,y)∈R^2 /0≤y≤2 and (√(3y))≤x≤(√(4−y^2 )) I =∫_0 ^2 (∫_(√(3y)) ^(√(4−y^2 )) (√(x^2 +y^2 ))dx)dy let find A(y)=∫_(√(3y)) ^(√(4−y^2 )) (√(x^2 +y^2 ))dx A(y) =_(x=ysh(t)) ∫_(argsh(((√3)/(√y)))) ^(argsh(((√(4−y^2 ))/y))) ych(t)y ch(t)dt = y^2 ∫_(ln(((√3)/(√y)) +(√(3/y^2 ))+1)) ^(ln(((√(4−y^2 ))/y) +(√((4−y^2 )/y^2 ))+1)) ((1+ch(2t))/2) dt =(y^2 /2){ln(((√(4−y^2 ))/y)+(2/y))−ln(((√3)/(√y)) +(√(3/y^2 ))+1)} +(y^2 /4)[sh(2t)]_(α(y)) ^(β(y)) =...+(y^2 /8)[ e^(2t) −e^(−2t) ]_(α(y)) ^(β(y)) =....+(y^2 /8){ (((√(4−y^2 ))/y) +(2/y))^2 −(((√3)/(√y)) +(√((3/y^2 )+1)))^(−2) } ⇒ A(y)=(y^2 /2){ln(((√(4−y^2 ))/y) +(2/y))−ln(((√3)/(√y)) +(√((3/y^2 )+1))) +(y^2 /8){ln(((√(4−y^2 ))/y) +(2/y))−ln(((√3)/(√y)) +(√((3/y^2 )+1)))^(−2) } ⇒ I =∫_0 ^2 A(y)dy ...be continued...$
$l e t I = \int \int_{D} \sqrt{x^{2} + y^{2}} d x d y w i t h D = {(x, y) \in R^{2} / 0 ⩽ y ⩽ 2 a n d$ $\sqrt{3 y} ⩽ x ⩽ \sqrt{4 - y^{2}}$ $I = \int_{0}^{2} (\int_{\sqrt{3 y}}^{\sqrt{4 - y^{2}}} \sqrt{x^{2} + y^{2}} d x) d y l e t f i n d A (y) = \int_{\sqrt{3 y}}^{\sqrt{4 - y^{2}}} \sqrt{x^{2} + y^{2}} d x$ $A (y) =_{x = y s h (t)} \int_{a r g s h (\frac{\sqrt{3}}{\sqrt{y}})}^{a r g s h (\frac{\sqrt{4 - y^{2}}}{y})} y c h (t) y c h (t) d t$ $= y^{2} \int_{l n (\frac{\sqrt{3}}{\sqrt{y}} + \sqrt{\frac{3}{y^{2}}} + 1)}^{l n (\frac{\sqrt{4 - y^{2}}}{y} + \sqrt{\frac{4 - y^{2}}{y^{2}}} + 1)} \frac{1 + c h (2 t)}{2} d t$ $= \frac{y^{2}}{2} {l n (\frac{\sqrt{4 - y^{2}}}{y} + \frac{2}{y}) - l n (\frac{\sqrt{3}}{\sqrt{y}} + \sqrt{\frac{3}{y^{2}}} + 1)}$ $+ \frac{y^{2}}{4} {[s h (2 t)]}_{α (y)}^{β (y)} = . . . + \frac{y^{2}}{8} {[e^{2 t} - e^{- 2 t}]}_{α (y)}^{β (y)}$ $= . . . . + \frac{y^{2}}{8} {{(\frac{\sqrt{4 - y^{2}}}{y} + \frac{2}{y})}^{2} - {(\frac{\sqrt{3}}{\sqrt{y}} + \sqrt{\frac{3}{y^{2}} + 1})}^{- 2}} \Rightarrow$ $A (y) = \frac{y^{2}}{2} {l n (\frac{\sqrt{4 - y^{2}}}{y} + \frac{2}{y}) - l n (\frac{\sqrt{3}}{\sqrt{y}} + \sqrt{\frac{3}{y^{2}} + 1})$ $+ \frac{y^{2}}{8} {l n (\frac{\sqrt{4 - y^{2}}}{y} + \frac{2}{y}) - l n {(\frac{\sqrt{3}}{\sqrt{y}} + \sqrt{\frac{3}{y^{2}} + 1})}^{- 2}} \Rightarrow$ $I = \int_{0}^{2} A (y) d y . . . b e c o n t i n u e d . . .$
Commented by Tawa1 last updated on 29/Nov/18

$God bless you sir$
Commented by maxmathsup by imad last updated on 01/Dec/18

$t h a n k y o u s i r .$
	Answered by MJS last updated on 28/Nov/18

	$(1) \int \sqrt{x^{2} + y^{2}} d x =$ $[t = arcsinh \frac{x}{y} \to x = y \sinh t \land d x = y \cosh t d t]$ $= \int y \cosh t \sqrt{y^{2} + y^{2} \sinh^{2} t} d t = y^{2} \int \cosh^{2} t d t =$ $= \frac{y^{2}}{2} \int \cosh 2 t d t + \frac{y^{2}}{2} \int d t = \frac{y^{2}}{4} \sinh 2 t + \frac{y^{2}}{2} t =$ $[y ⩾ 0]$ $= \frac{x}{2} \sqrt{x^{2} + y^{2}} + \frac{y^{2}}{2} arcsinh \frac{x}{y}$ $\underset{\sqrt{3 y}}{\int^{\sqrt{4 - y^{2}}}} \sqrt{x^{2} + y^{2}} d x = \sqrt{4 - y^{2}} + \frac{y^{2}}{2} arcsinh \frac{\sqrt{4 - y^{2}}}{y} - \frac{y}{2} \sqrt{3 (y + 3)} - \frac{y^{2}}{2} arcsinh \sqrt{\frac{3}{y}}$ $(2.1) \int \sqrt{4 - y^{2}} d y =$ $[u = \arcsin \frac{y}{2} \to y = 2 \sin u \land d y = 2 \cos u d u]$ $= \int 2 \cos u \sqrt{4 - {4 \sin}^{2} u} d u = 4 \int \cos^{2} u d u =$ $= 2 \int \cos 2 u d u + 2 \int d u = \sin 2 u + 2 u =$ $= \frac{y}{2} \sqrt{4 - y^{2}} + 2 \arcsin \frac{y}{2}$ $(2.2) \int \frac{y^{2}}{2} arcsinh \frac{\sqrt{4 - y^{2}}}{y} d y =$ $[\begin{matrix} \int f^{'} g = f g - \int {f g}^{'} with : f^{'} = \frac{y^{2}}{2} \to f = \frac{y^{3}}{6} \\ g = arcsinh \frac{\sqrt{4 - y^{2}}}{y} \to g^{'} = - \frac{2}{y \sqrt{4 - y^{2}}} \end{matrix}]$ $= \frac{y^{3}}{6} arcsinh \frac{\sqrt{4 - y^{2}}}{y} + \frac{1}{3} \int \frac{y^{2}}{\sqrt{4 - y^{2}}} d y =$ $\frac{1}{3} \int \frac{y^{2}}{\sqrt{4 - y^{2}}} d y = \frac{1}{3} \int \frac{y^{2} - 4 + 4}{\sqrt{4 - y^{2}}} d y =$ $= - \frac{1}{3} \int \sqrt{4 - y^{2}} d y + \frac{4}{3} \int \frac{d y}{\sqrt{4 - y^{2}}} =$ $= - \frac{y}{6} \sqrt{4 - y^{2}} + \frac{2}{3} \arcsin \frac{y}{2}$ $= \frac{y^{3}}{6} arcsinh \frac{\sqrt{4 - y^{2}}}{y} - \frac{y}{6} \sqrt{4 - y^{2}} + \frac{2}{3} \arcsin \frac{y}{2}$ $(2.3) \int - \frac{y}{2} \sqrt{3 (y + 3)} d y = - \frac{\sqrt{3}}{2} \int y \sqrt{y + 3} d y =$ $[v = y + 3 \to d y = d v]$ $= - \frac{\sqrt{3}}{2} \int (v - 3) \sqrt{v} d v = \frac{3 \sqrt{3}}{2} \int v^{\frac{1}{2}} d v - \frac{\sqrt{3}}{2} \int v^{\frac{3}{2}} d v =$ $= \sqrt{3} v^{\frac{3}{2}} - \frac{\sqrt{3}}{5} v^{\frac{5}{2}} = \sqrt{3} {(y + 3)}^{\frac{3}{2}} - \frac{\sqrt{3}}{5} {(y + 3)}^{\frac{5}{2}} = \frac{\sqrt{3}}{5} (2 - y) {(y + 3)}^{\frac{3}{2}}$ $(2.4) \int - \frac{y^{2}}{2} arcsinh \sqrt{\frac{3}{y}} d y = - \frac{1}{2} \int y^{2} arcsinh \sqrt{\frac{3}{y}} d y =$ $[w = \frac{y^{3}}{3} \to d x = \frac{d w}{y^{2}}]$ $= - \frac{1}{2} \int arcsinh \frac{\sqrt[3]{3}}{\sqrt[6]{w}} d w =$ $[\begin{matrix} \int f^{'} g = f g - \int {f g}^{'} with : f^{'} = 1 \to f = w \\ g = arcsinh \frac{\sqrt[3]{3}}{\sqrt[6]{w}} \to g^{'} = - \frac{\sqrt[3]{3}}{6 w \sqrt{\sqrt[3]{w} + \sqrt[3]{9}}} \end{matrix}]$ $= - \frac{w}{2} arcsinh \frac{\sqrt[3]{3}}{\sqrt[6]{w}} - \frac{\sqrt[3]{3}}{12} \int \frac{d w}{\sqrt{\sqrt[3]{w} + \sqrt[3]{9}}}$ $- \frac{\sqrt[3]{3}}{12} \int \frac{d w}{\sqrt{\sqrt[3]{w} + \sqrt[3]{9}}} =$ $[z = \sqrt[3]{w} + \sqrt[3]{9} \to d w = 3 (z - \sqrt[3]{9}) d z]$ $= - \frac{\sqrt[3]{3}}{4} \int z^{\frac{3}{2}} d z + \frac{3}{2} \int z^{\frac{1}{2}} d z - \frac{3 \sqrt[3]{9}}{4} \int z^{- \frac{1}{2}} d z =$ $= - \frac{\sqrt[3]{3}}{10} z^{\frac{5}{2}} + z^{\frac{3}{2}} - \frac{3 \sqrt[3]{9}}{2} z^{\frac{1}{2}} = (- \frac{\sqrt[3]{3}}{10} \sqrt[3]{w^{2}} + \frac{2}{5} \sqrt[3]{w} - \frac{4 \sqrt[3]{9}}{5}) \sqrt{\sqrt[3]{w} + \sqrt[3]{9}}$ $= - \frac{w}{2} arcsinh \frac{\sqrt[3]{3}}{\sqrt[6]{w}} - (\frac{\sqrt[3]{3}}{10} \sqrt[3]{w^{2}} - \frac{2}{5} \sqrt[3]{w} + \frac{4 \sqrt[3]{9}}{5}) \sqrt{\sqrt[3]{w} + \sqrt[3]{9}} =$ $= - \frac{y^{3}}{6} arcsinh \frac{\sqrt[3]{9}}{y} - \frac{1}{30} (y^{2} - 4 y + 24) \sqrt{3 (y + 3)}$ $\underset{0}{\int^{2}} (\underset{\sqrt{3 y}}{\int^{\sqrt{4 - y^{2}}}} \sqrt{x^{2} + y^{2}} d x) d y = \frac{4 π}{3} - \frac{4}{3} arcsinh \frac{\sqrt[3]{9}}{2} - \frac{2 \sqrt{15}}{3} - \frac{6}{5} \approx - . 805740$
	Commented by MJS last updated on 28/Nov/18

	$. . . please someone check for typos . {it}^{'} s 3 a . m .$ $and I^{'} m really tired . . .$
	Commented by maxmathsup by imad last updated on 28/Nov/18

	$t h a n k y o u s i r f o r t h i s h a r d w o r k t h i s i s t h e w a y .$
	Commented by MJS last updated on 28/Nov/18

	${you}^{'} re welcome$
	Commented by Tawa1 last updated on 29/Nov/18

	$God bless you sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum