Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 48955 by Abdulhafeez Abu qatada last updated on 30/Nov/18

$$Evaluate\underset{0}{\stackrel{\frac{\sqrt{3}}{4}}{\int }}\frac{2x{\sin }^{-1}\left(2x\right)}{\sqrt{1-4x^2}}dx$$

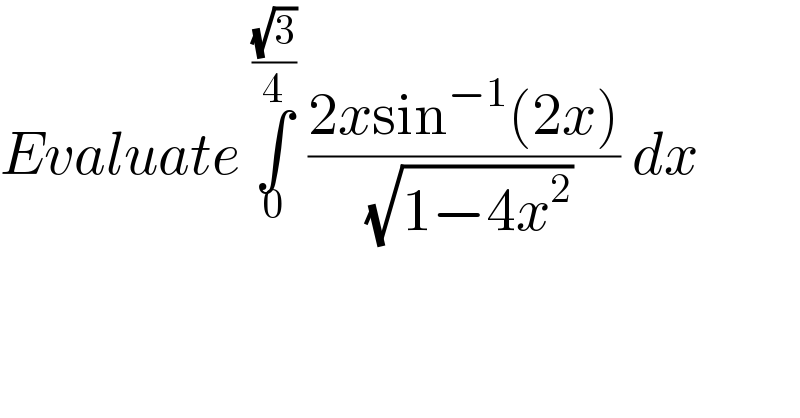
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Nov/18

$$2x=sin\theta 2dx=cos\theta d\theta$$$${\int }_0^{\frac{\pi }{3}}\frac{sin\theta \times \theta }{\sqrt{1-{sin}^2\theta }}\times \frac{cos\theta d\theta }{2}$$$$\frac{1}{2}{\int }_0^{\frac{\pi }{3}}\theta sin\theta d\theta$$$$I=\int \theta sin\theta d\theta$$$$=\theta \int sin\theta d\theta -\int [\frac{d\theta }{d\theta }\int sin\theta d\theta ]d\theta$$$$=-\theta cos\theta -\int -cos\theta d\theta$$$$=-\theta cos\theta +sin\theta +c$$$$sorequiredintregalis$$$$\frac{1}{2}\mid -\theta cos\theta +sin\theta {\mid }_0^{\frac{\pi }{3}}$$$$=\frac{1}{2}\left[(-\frac{\pi }{3}\times \frac{1}{2}+\frac{\sqrt{3}}{2})\right]$$$$=\frac{-\pi }{12}+\frac{\sqrt{3}}{4}$$

Answered by MJS last updated on 30/Nov/18

$$u^{\prime }=\frac{2x}{\sqrt{1-4x^2}}\Rightarrow u=-\frac{\sqrt{1-4x^2}}{4}$$$$v=\arcsin 2x\Rightarrow v^{\prime }=\frac{2}{\sqrt{1-x^2}}$$$$\int u^{\prime }v=uv-\int {uv}^{\prime }$$$$\int \frac{2x\arcsin 2x}{\sqrt{1-4x^2}}=x-\frac{\sqrt{1-4x^2}}{2}\arcsin 2x$$$$\underset{0}{\stackrel{\frac{\sqrt{3}}{4}}{\int }}\frac{2x\arcsin 2x}{\sqrt{1-4x^2}}dx=\frac{3\sqrt{3}-\pi }{12}$$

Answered by Abdulhafeez Abu qatada last updated on 02/Dec/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com