Question and Answers Forum
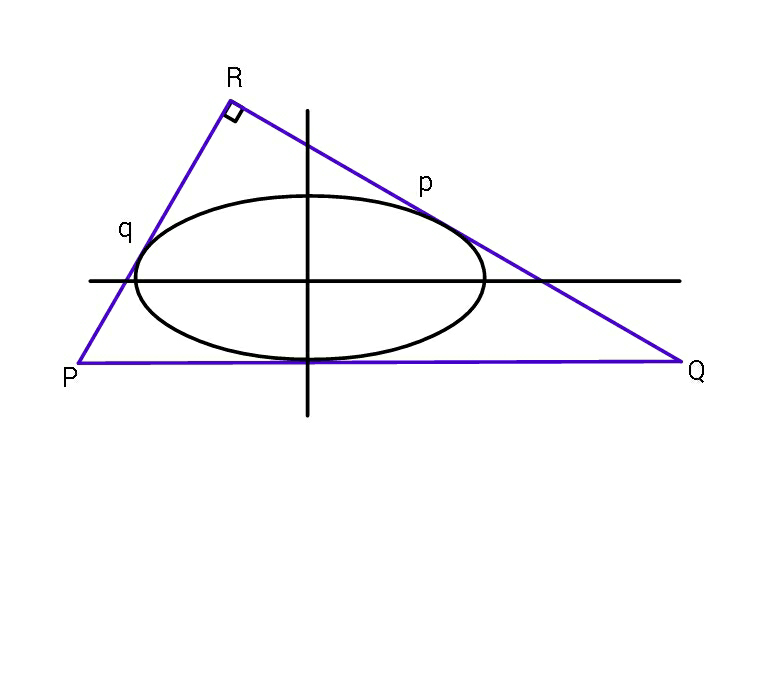
Question Number 49020 by ajfour last updated on 01/Dec/18
Commented by ajfour last updated on 01/Dec/18

Commented by ajfour last updated on 01/Dec/18
Answered by mr W last updated on 01/Dec/18
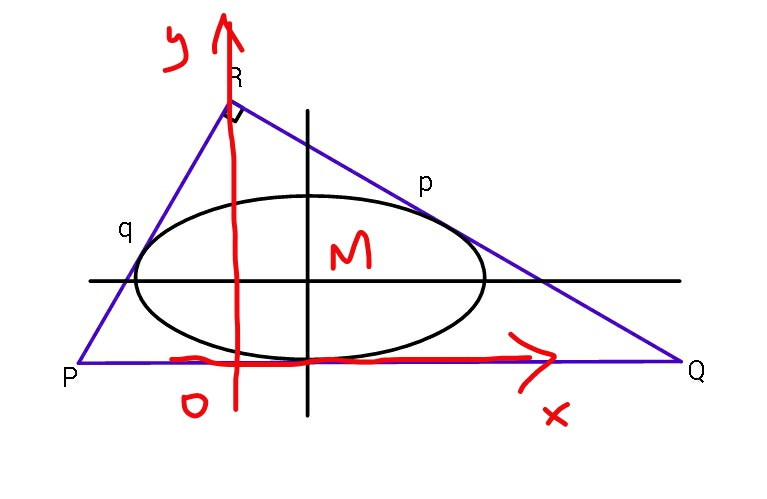
Commented by mr W last updated on 02/Dec/18
![let m=(q/p), λ=m^2 −1 R(0,d) where d=((pq)/(√(p^2 +q^2 )))=altitude of triangle M(h,b)=center of ellipse eqn. of ellipse: (((x−h)^2 )/a^2 )+(((y−b)^2 )/b^2 )=1 eqn. of RQ: y=−mx+d a^2 m^2 +b^2 =(d−mh−b)^2 ← tangent of ellipsr a^2 m^2 =(d−mh)^2 −2(d−mh)b a^2 m^2 +2(d−mh)b=(d−mh)^2 ...(i) eqn. of RP: y=(1/m)x+d (a^2 /m^2 )+b^2 =(d+(h/m)−b)^2 ← tangent of ellipse (a^2 /m^2 )=(d+(h/m))^2 −2(d+(h/m))b a^2 =(md+h)^2 −2m(md+h)b a^2 +2m(md+h)b=(md+h)^2 ...(ii) case 1: p=q, i.e. m=1, h=0 from (i) or (ii) we get a^2 +2db=d^2 ⇒b=((d^2 −a^2 )/(2d)) area of ellipse A=πab=((π(d^2 a−a^3 ))/(2d)) (dA/da)=0⇒d^2 −3a^2 =0⇒a=(d/(√3))⇒b=(d/3) case 2: p≠q, i.e. m≠1 (ii)×m^2 −(i): 2[m^4 d+m^3 h−d+mh]b=(m^2 d+mh+d−mh)(m^2 d+mh−d+mh) 2[(m^2 −1)d+mh]b=[(m^2 −1)d+2mh]d ⇒b=(([(m^2 −1)d+2mh]d)/(2[(m^2 −1)d+mh]))=(([(m^2 −1)+((2mh)/d)]d)/(2[(m^2 −1)+((mh)/d)])) ⇒b=(d/2)(((λ+2μ)/(λ+μ))) with μ=((mh)/d)=((h(√(p^2 +q^2 )))/p^2 ) (i)×m(md+h)−(ii)×(d−mh): a^2 [m^3 (md+h)−(d−mh)]=m(md+h)(d−mh)^2 −(d−mh)(md+h)^2 a^2 [(m^2 −1)d+mh]=(mh−d)(md+h)h ⇒a^2 =(((mh−d)(md+h)h)/((m^2 −1)d+mh))=(d^2 /m^2 )×(((((mh)/d)−1)(m^2 +((mh)/d))((mh)/d))/([(m^2 −1)+((mh)/d)])) ⇒a^2 =(d^2 /m^2 )×((μ(μ−1)(m^2 +μ))/(λ+μ)) P=((4m^2 )/d^2 )×a^2 b^2 =((μ(μ−1)(λ+1+μ)(λ+2μ)^2 )/((λ+μ)^3 )) since area of ellipse is A=πab, max. A means also max. P. (dP/dμ)=(((μ−1)(λ+1+μ)(λ+2μ)^2 +μ(λ+1+μ)(λ+2μ)^2 +μ(μ−1)(λ+2μ)^2 +4μ(μ−1)(λ+1+μ)(λ+2μ))/((λ+μ)^3 ))−((3μ(μ−1)(λ+1+μ)(λ+2μ)^2 )/((λ+μ)^4 ))=0 6μ^4 +13λμ^3 +(9λ^2 −2λ−2)μ^2 +(2λ^3 −3λ^2 −3λ)μ−(λ^3 +λ^2 )=2μ^4 +λμ^3 −(λ^2 +2λ+2)μ^2 +(λ^2 +λ)μ ⇒4μ^4 +12λμ^3 +10λ^2 μ^2 +2λ(λ^2 −2λ−2)μ−λ^2 (λ+1)=0 we solve this eqn. for μ=f(λ) ⇒a=(d/m)(√((μ(μ−1)(m^2 +μ))/(m^2 +μ−1))) ⇒b=(d/2)(1+(μ/(m^2 +μ−1))) ⇒h=((μd)/m)=((μp^2 )/(√(p^2 +q^2 )))](Q49047.png)
Commented by ajfour last updated on 02/Dec/18

Commented by mr W last updated on 02/Dec/18
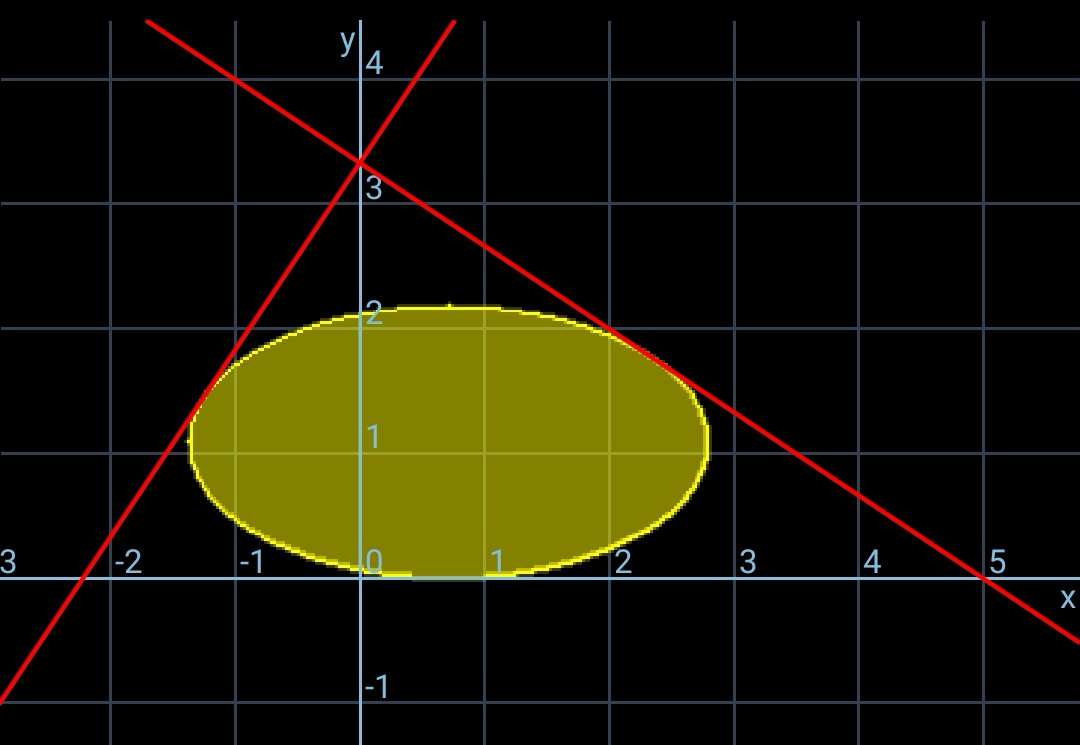
Commented by mr W last updated on 02/Dec/18
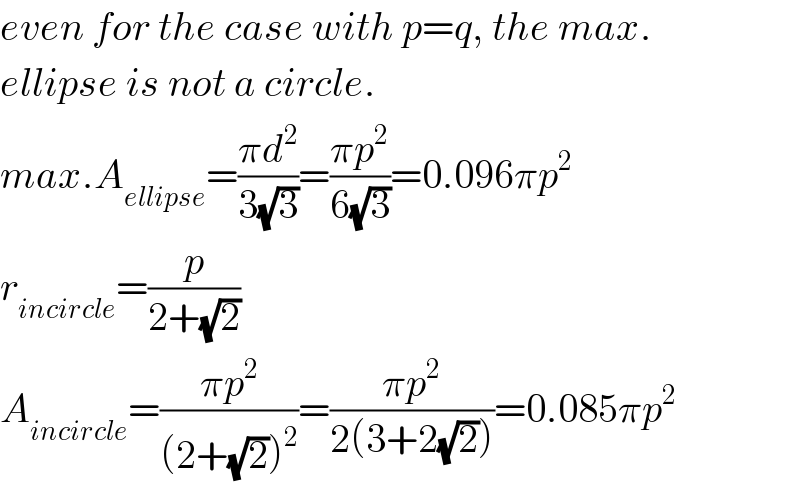
Commented by mr W last updated on 02/Dec/18
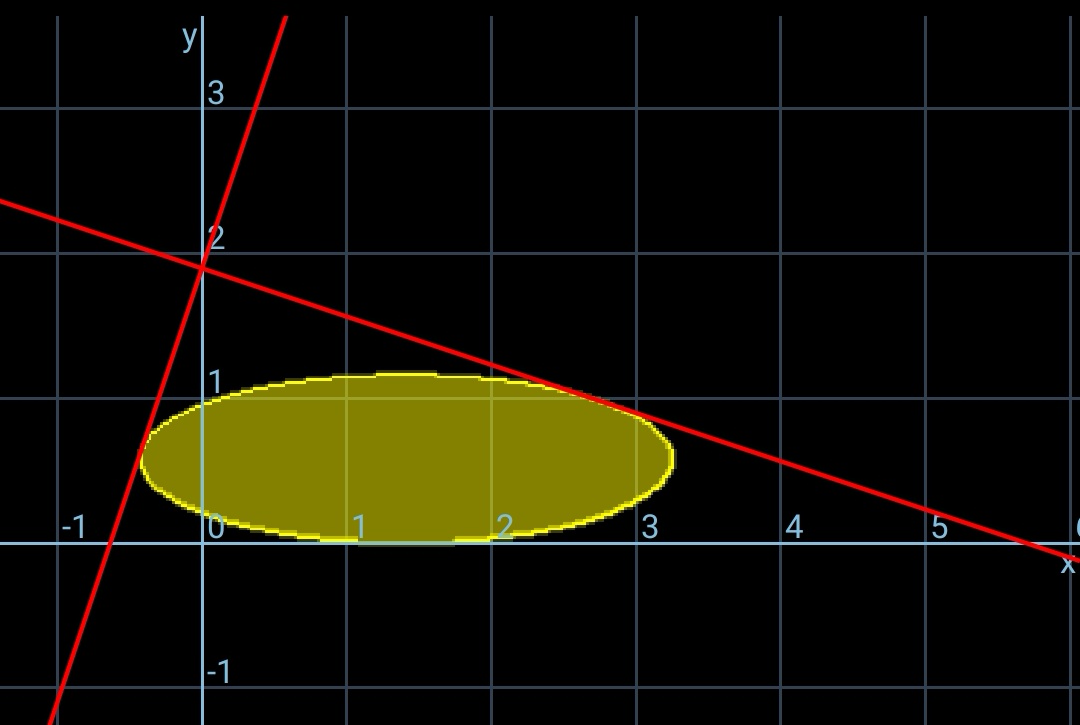
Commented by mr W last updated on 02/Dec/18
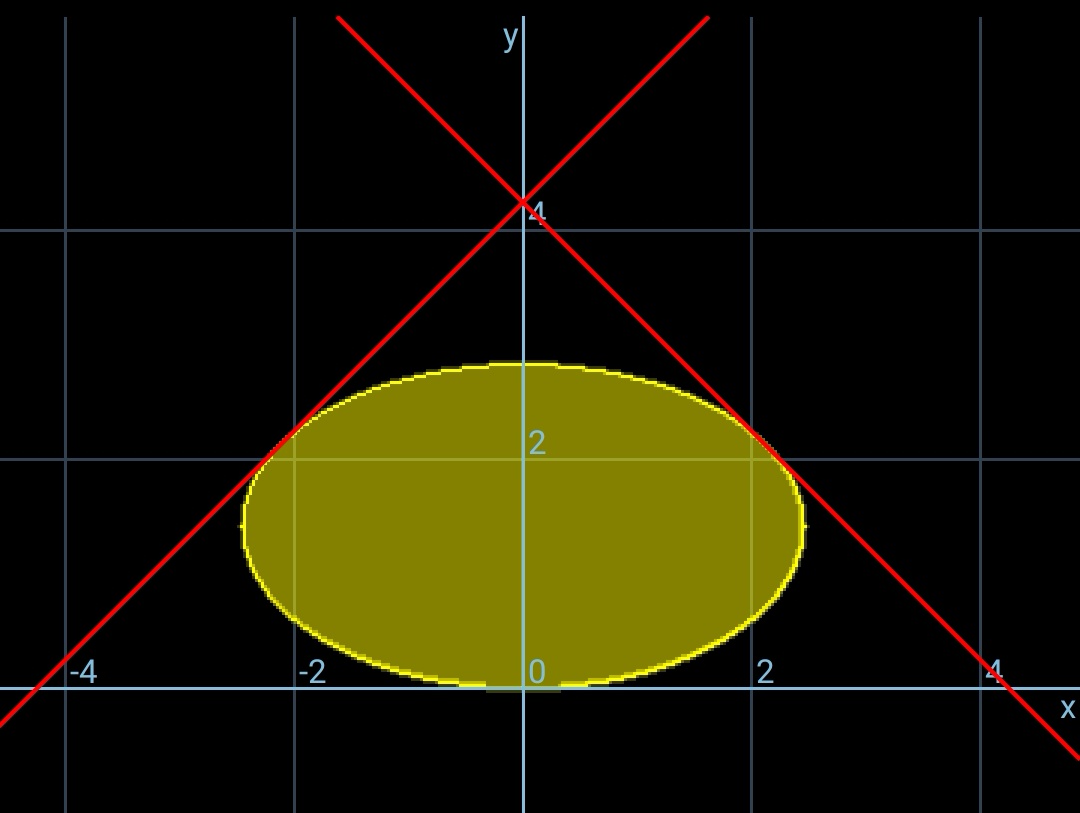
Commented by mr W last updated on 02/Dec/18
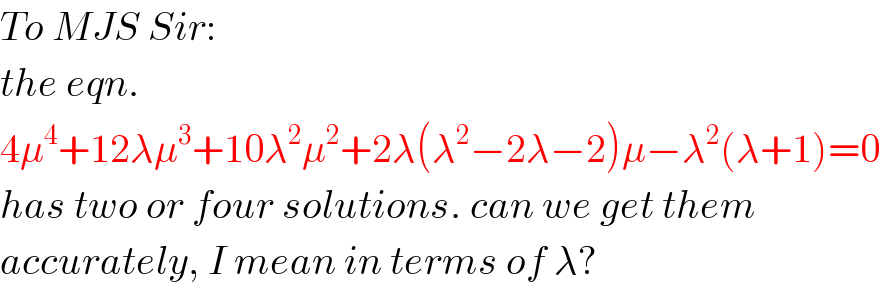
Commented by ajfour last updated on 02/Dec/18

Commented by mr W last updated on 02/Dec/18
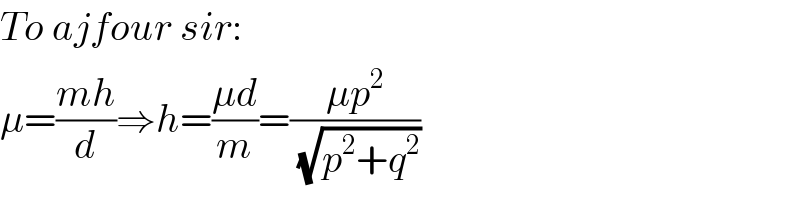
Commented by mr W last updated on 02/Dec/18
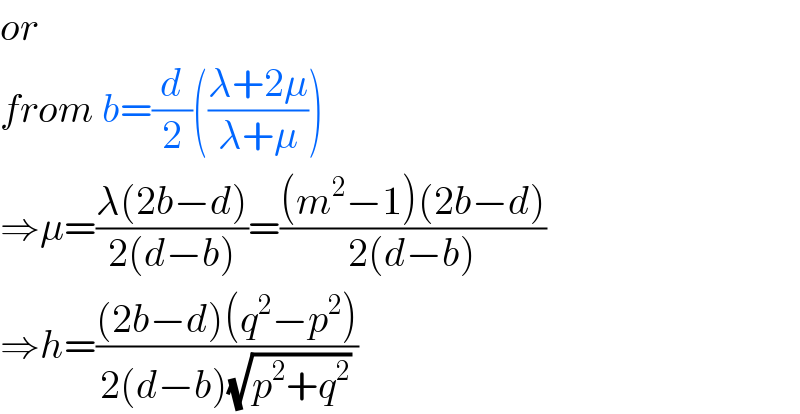
Commented by MJS last updated on 02/Dec/18
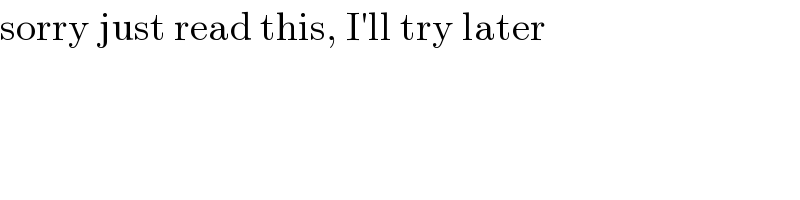
Commented by MJS last updated on 02/Dec/18
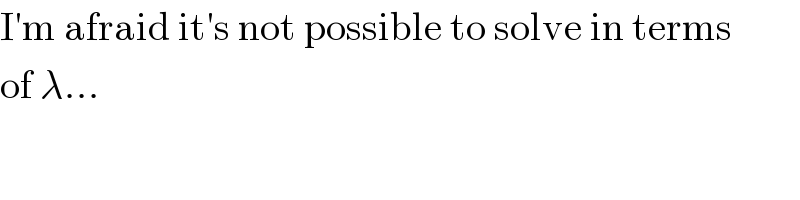
Commented by mr W last updated on 03/Dec/18
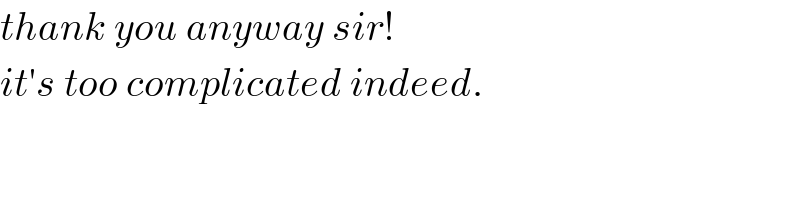
Answered by ajfour last updated on 03/Dec/18
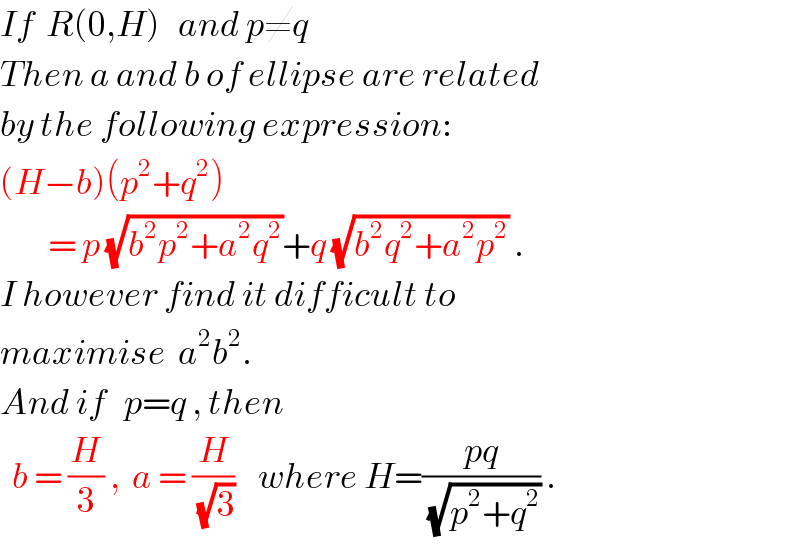
Commented by mr W last updated on 03/Dec/18
![(H−b)(p^2 +q^2 )= p (√(b^2 p^2 +a^2 q^2 ))+q (√(b^2 q^2 +a^2 p^2 )) (aH−ab)(p^2 +q^2 )= p (√(a^2 b^2 p^2 +a^4 q^2 ))+q (√(a^2 b^2 q^2 +a^4 p^2 )) (aH−S)(p^2 +q^2 )= p (√(S^2 p^2 +a^4 q^2 ))+q (√(S^2 q^2 +a^4 p^2 )) with S=ab (dS/da)=0 H(p^2 +q^2 )= p ((4a^3 q^2 )/(2(√(S^2 p^2 +a^4 q^2 ))))+q((4a^3 p^2 )/(2 (√(S^2 q^2 +a^4 p^2 )) )) H(p^2 +q^2 )=2pqa^2 [ (q/(√(b^2 p^2 +a^2 q^2 )))+(p/( (√(b^2 q^2 +a^2 p^2 )) ))] H(p^2 +q^2 )=2pqa^2 [ ((q (√(b^2 q^2 +a^2 p^2 ))+p(√(b^2 p^2 +a^2 q^2 )))/(√((b^2 p^2 +a^2 q^2 )(b^2 q^2 +a^2 p^2 ))))] H(p^2 +q^2 )=2pqa^2 [ (((H−b)(p^2 +q^2 ))/(√((b^2 p^2 +a^2 q^2 )(b^2 q^2 +a^2 p^2 ))))] H=2pqa^2 [ (((H−b))/(√((b^2 p^2 +a^2 q^2 )(b^2 q^2 +a^2 p^2 ))))] let β=(b/a) ((pq)/(√(p^2 +q^2 )))=2pq[ (((H−b))/(√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))))] (1/(√(p^2 +q^2 )))=2[ (((H−b))/(√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))))] b=H[1−(1/(2H))(√(((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))/(p^2 +q^2 )))] (H/b)=(1/([1−(1/(2H))(√(((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))/(p^2 +q^2 )))])) =(1/(1−((√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 )))/(2pq)))) ((H/b)−1)(p^2 +q^2 )β= p (√(β^2 p^2 +q^2 ))+q (√(β^2 q^2 +p^2 )) {(1/(1−((√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 )))/(2pq))))−1}(p^2 +q^2 )β= p (√(β^2 p^2 +q^2 ))+q (√(β^2 q^2 +p^2 )) with m=(q/p) ⇒{(1/(1−((√((β^2 +m^2 )(β^2 m^2 +1)))/2)))−1}(1+m^2 )β= (√(β^2 +m^2 ))+m (√(β^2 m^2 +1)) ⇒β=....](Q49135.png)
Commented by mr W last updated on 03/Dec/18

Commented by ajfour last updated on 03/Dec/18