Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 4911 by FilupSmith last updated on 21/Mar/16

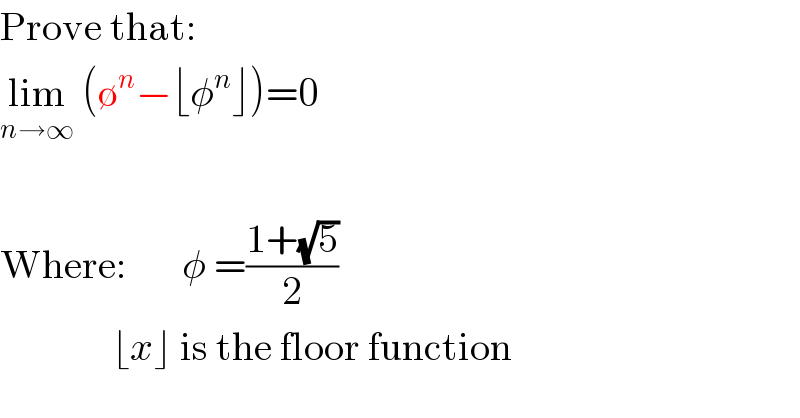
Prove that: lim_(n→∞) (∅^n −⌊φ^n ⌋)=0 Where: φ =((1+(√5))/2) ⌊x⌋ is the floor function

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\emptyset^{{n}} −\lfloor\phi^{{n}} \rfloor\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Where}:\:\:\:\:\:\:\:\phi\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\lfloor{x}\rfloor\:\mathrm{is}\:\mathrm{the}\:\mathrm{floor}\:\mathrm{function} \\ $$

Commented by Yozzii last updated on 21/Mar/16

Let f(x)=a^x where a>1,x∈R^+ . ⇒f^′ (x)=a^x lna. a>1⇒lna>0 and a>1⇒a^x >1>0 for x∈R^+ . So, f^′ (x)>0 for all x∈R^+ . Hence, f is perpetually increasing as x increases. Treating x as an natural number n, f(n)=a^n is increasing for all n∈N. Now, φ≈1.618033989>1. ⇒φ^n >1⇒f(n)>1.⇒⌊f(n)⌋≥1>0 for all n∈N. So, lim_(n→∞) ⌊f(n)⌋≠0.

$${Let}\:{f}\left({x}\right)={a}^{{x}} \:{where}\:{a}>\mathrm{1},{x}\in\mathbb{R}^{+} . \\ $$$$\Rightarrow{f}^{'} \left({x}\right)={a}^{{x}} {lna}. \\ $$$${a}>\mathrm{1}\Rightarrow{lna}>\mathrm{0}\:{and}\:{a}>\mathrm{1}\Rightarrow{a}^{{x}} >\mathrm{1}>\mathrm{0}\:{for}\:{x}\in\mathbb{R}^{+} . \\ $$$${So},\:{f}^{'} \left({x}\right)>\mathrm{0}\:{for}\:{all}\:{x}\in\mathbb{R}^{+} .\:{Hence}, \\ $$$${f}\:{is}\:{perpetually}\:{increasing}\:{as}\:{x}\:{increases}. \\ $$$${Treating}\:{x}\:{as}\:{an}\:{natural}\:{number}\:{n}, \\ $$$${f}\left({n}\right)={a}^{{n}} \:{is}\:{increasing}\:{for}\:{all}\:{n}\in\mathbb{N}. \\ $$$${Now},\:\phi\approx\mathrm{1}.\mathrm{618033989}>\mathrm{1}. \\ $$$$\Rightarrow\phi^{{n}} >\mathrm{1}\Rightarrow{f}\left({n}\right)>\mathrm{1}.\Rightarrow\lfloor{f}\left({n}\right)\rfloor\geqslant\mathrm{1}>\mathrm{0}\:{for}\: \\ $$$${all}\:{n}\in\mathbb{N}.\:{So},\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor{f}\left({n}\right)\rfloor\neq\mathrm{0}.\: \\ $$$$ \\ $$$$ \\ $$

Commented by FilupSmith last updated on 21/Mar/16

sorry i made a horrible typo on my question

$${sorry}\:{i}\:{made}\:{a}\:{horrible}\:{typo}\:{on}\:{my}\:{question} \\ $$

Answered by Algebro last updated on 21/Mar/16

∅≈1.618 lim_(n→∞) (⌊1.6^n ⌋)=∞ because lim_(n→∞) (1.6^n )=∞ I am srry bro :/ peace Algebro

$$ \\ $$$$\emptyset\approx\mathrm{1}.\mathrm{618} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\lfloor\mathrm{1}.\mathrm{6}^{{n}} \rfloor\right)=\infty \\ $$$$\mathrm{because} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}.\mathrm{6}^{{n}} \right)=\infty \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{srry}\:\mathrm{bro}\::/ \\ $$$$\mathrm{peace}\:\boldsymbol{\mathrm{Algebro}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com