
Question Number 49177 by rahul 19 last updated on 04/Dec/18
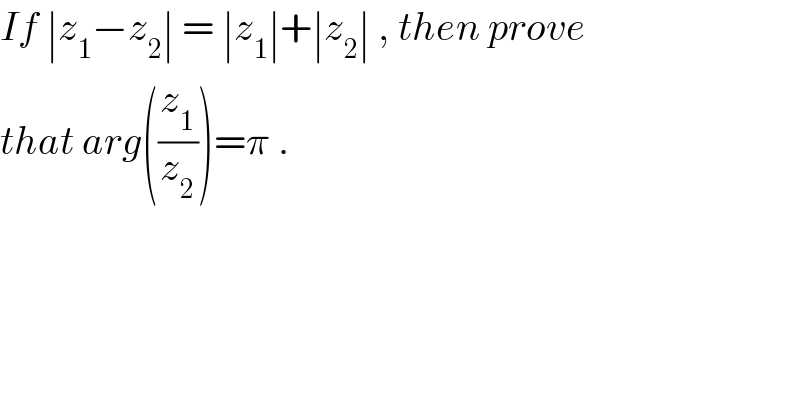
$${If}\:\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid\:=\:\mid{z}_{\mathrm{1}} \mid+\mid{z}_{\mathrm{2}} \mid\:,\:{then}\:{prove}\: \\ $$$${that}\:{arg}\left(\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\right)=\pi\:. \\ $$
Answered by MJS last updated on 04/Dec/18
![z_1 =pe^(iα) ; z_2 =qe^(iβ) ∣z_1 −z_2 ∣=(√(p^2 +q^2 −2pq cos (α−β))) ∣z_1 ∣+∣z_2 ∣=∣p∣+∣q∣ ⇒ −2pqcos (α−β)=2pq ⇒ cos (α−β)=−1 ⇒ α−β=π [(z_1 /z_2 )=(p/q)e^(i(α−β)) ]](Q49181.png)
$${z}_{\mathrm{1}} ={p}\mathrm{e}^{\mathrm{i}\alpha} ;\:\mathrm{z}_{\mathrm{2}} ={q}\mathrm{e}^{\mathrm{i}\beta} \\ $$$$\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\:\mathrm{cos}\:\left(\alpha−\beta\right)} \\ $$$$\mid{z}_{\mathrm{1}} \mid+\mid{z}_{\mathrm{2}} \mid=\mid{p}\mid+\mid{q}\mid \\ $$$$\Rightarrow\:−\mathrm{2}{pq}\mathrm{cos}\:\left(\alpha−\beta\right)=\mathrm{2}{pq} \\ $$$$\Rightarrow\:\mathrm{cos}\:\left(\alpha−\beta\right)=−\mathrm{1}\:\Rightarrow\:\alpha−\beta=\pi \\ $$$$\left[\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }=\frac{{p}}{{q}}\mathrm{e}^{\mathrm{i}\left(\alpha−\beta\right)} \right] \\ $$
Commented by MJS last updated on 04/Dec/18

$$...\mathrm{corrected} \\ $$
Commented by rahul 19 last updated on 04/Dec/18
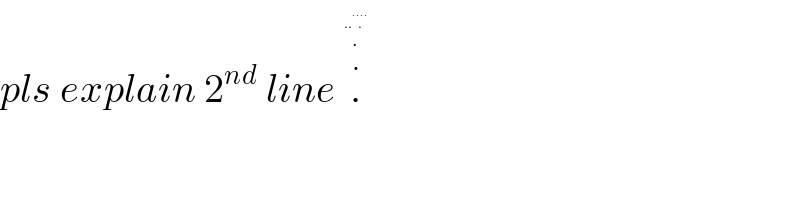
$${pls}\:{explain}\:\mathrm{2}^{{nd}} \:{line}\:\overset{\overset{\overset{..\overset{....} {.}} {.}} {.}} {.} \\ $$
Commented by MJS last updated on 04/Dec/18
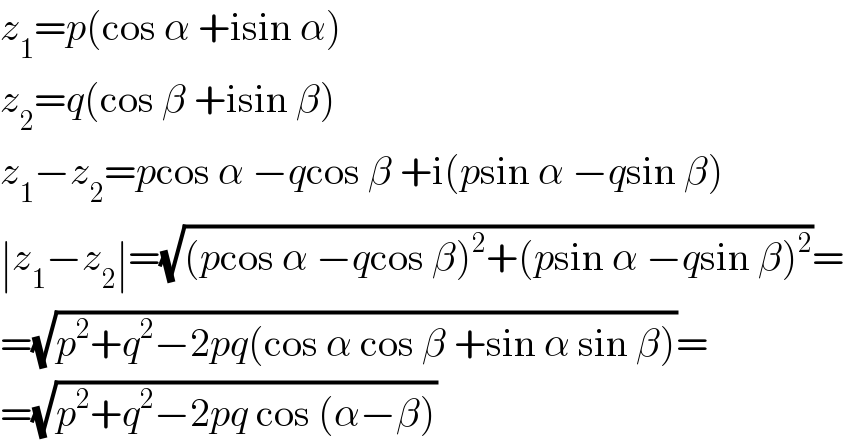
$${z}_{\mathrm{1}} ={p}\left(\mathrm{cos}\:\alpha\:+\mathrm{isin}\:\alpha\right) \\ $$$${z}_{\mathrm{2}} ={q}\left(\mathrm{cos}\:\beta\:+\mathrm{isin}\:\beta\right) \\ $$$${z}_{\mathrm{1}} −{z}_{\mathrm{2}} ={p}\mathrm{cos}\:\alpha\:−{q}\mathrm{cos}\:\beta\:+\mathrm{i}\left({p}\mathrm{sin}\:\alpha\:−{q}\mathrm{sin}\:\beta\right) \\ $$$$\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid=\sqrt{\left({p}\mathrm{cos}\:\alpha\:−{q}\mathrm{cos}\:\beta\right)^{\mathrm{2}} +\left({p}\mathrm{sin}\:\alpha\:−{q}\mathrm{sin}\:\beta\right)^{\mathrm{2}} }= \\ $$$$=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:+\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\right)}= \\ $$$$=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\:\mathrm{cos}\:\left(\alpha−\beta\right)} \\ $$
Commented by rahul 19 last updated on 04/Dec/18
thank you sir! ����
Commented by MJS last updated on 04/Dec/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
