
Question and Answers Forum
Question Number 49183 by ajfour last updated on 04/Dec/18
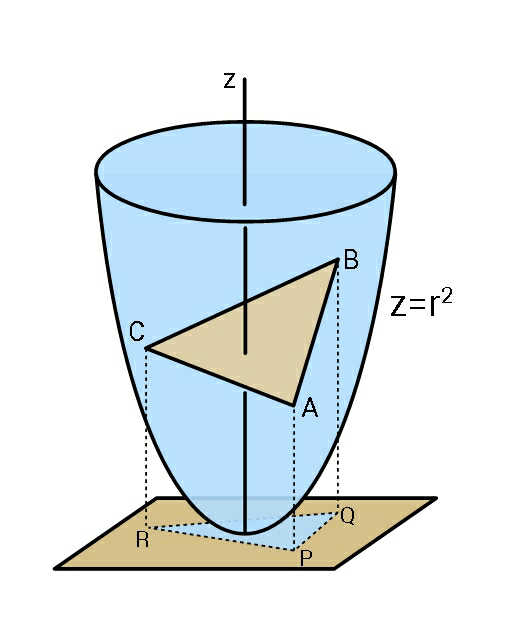
Commented by ajfour last updated on 04/Dec/18
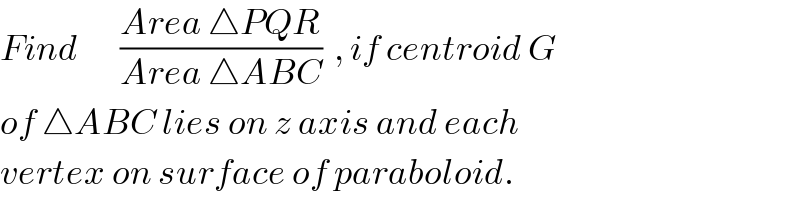
Commented by mr W last updated on 04/Dec/18
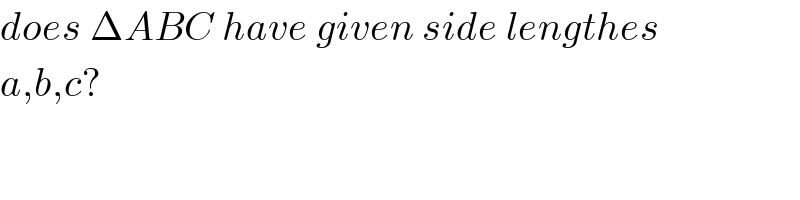
Commented by ajfour last updated on 04/Dec/18

Answered by mr W last updated on 05/Dec/18
![z=kr^2 with k=1 lengthes of medians of ΔABC: AG=(2/3)m_a =g_a =((√(2(b^2 +c^2 )−a^2 ))/3) BG=(2/3)m_b =g_b =((√(2(c^2 +a^2 )−b^2 ))/3) CG=(2/3)m_c =g_c =((√(2(a^2 +b^2 )−c^2 ))/3) let z_G =h let z_A =z_G +AG sin α=h+g_a sin α let z_B =z_G +BG sin β=h+g_b sin β we have three unknowns: h,α,β. r_A =AG cos α=g_a cos α r_B =BG cos β=g_b cos β z_A =kr_A ^2 ⇒h+g_a sin α=kg_a ^2 cos^2 α ⇒sin^2 α+(1/(kg_a )) sin α+(h/(kg_a ^2 ))−1=0 ...(i) similarly ⇒sin^2 β+(1/(kg_b )) sin β+(h/(kg_b ^2 ))−1=0 ...(ii) ⇒sin^2 γ+(1/(kg_c )) sin γ+(h/(kg_c ^2 ))−1=0 z_(B′) =z_G −B′G sin β=h−(1/3)m_b sin β z_(B′) =(1/2)(z_A +z_C ) z_C =2z_(B′) −z_A =2h−(2/3)m_b sin β−h−(2/3)m_a sin α ⇒z_C =h−(2/3)(m_a sin α+m_b sin β) z_C =h+(2/3)m_c sin γ ⇒(2/3)m_c sin γ=−(2/3)(m_a sin α+m_b sin β) ⇒ sin γ=−(1/g_c )(g_a sin α+g_b sin β) ⇒k(g_a sin α+g_b sin β)^2 −(g_a sin α+g_b sin β)+h−kg_c ^2 =0 ...(iii) from (i) and (ii): k(g_a ^2 sin^2 α−g_b ^2 sin^2 β)+(g_a sin α−g_b sin β)−k(g_a ^2 −g_b ^2 )=0 (1+kg_a sin α+kg_b sin β)(g_a sin α−g_b sin β)=k(g_a ^2 −g_b ^2 ) from (i) and (iii): k[g_a ^2 sin^2 α−(g_a sin α+g_b sin β)^2 ]+[g_a sin α+(g_a sin α+g_b sin β)]−k(g_a ^2 −g_c ^2 )=0 (1−kg_b sin β)(2g_a sin α+g_b sin β)=k(g_a ^2 −g_c ^2 ) we can solve (nummerically) { ((((1/k)+g_a sin α+g_b sin β)(g_a sin α−g_b sin β)=g_a ^2 −g_b ^2 )),((((1/k)−g_b sin β)(2g_a sin α+g_b sin β)=g_a ^2 −g_c ^2 )) :} for sin α and sin β. note: there can be more than one solution! with sin α and sin β we get sin γ from g_a sin α+g_b sin β+g_c sin γ=0 let e_a ,e_b ,e_c =projection of AG,BG,CG e_a =g_a cos α=g_a (√(1−sin^2 α)) e_b =g_b cos β=g_b (√(1−sin^2 β)) e_c =g_c cos γ=g_c (√(1−sin^2 γ)) Δ_(PQR) =((3(√((e_a +e_b +e_c )(−e_a +e_b +e_c )(e_a −e_b +e_c )(e_a +e_b −e_c ))))/4) Δ_(ABC) =((√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))/4) (Δ_(PQR) /Δ_(ABC) )=((3(√((e_a +e_b +e_c )(−e_a +e_b +e_c )(e_a −e_b +e_c )(e_a +e_b −e_c ))))/(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c))))](Q49228.png)
Commented by mr W last updated on 04/Dec/18
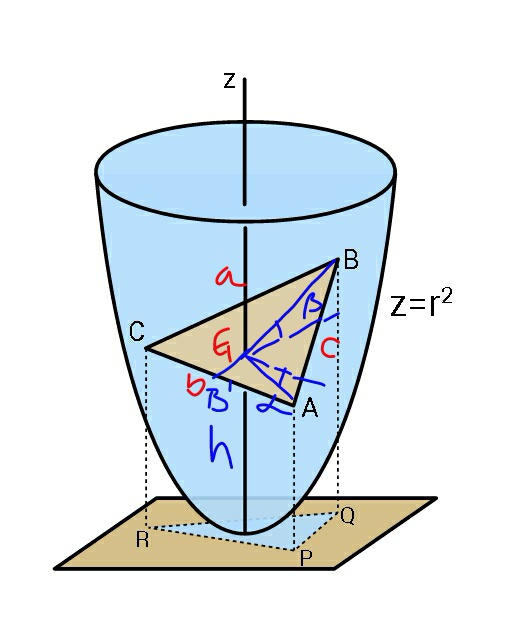
Commented by ajfour last updated on 06/Dec/18

Commented by mr W last updated on 06/Dec/18

