
Question and Answers Forum
Question Number 49187 by Rahul kharade last updated on 04/Dec/18

Answered by MJS last updated on 04/Dec/18
![∫((sin x)/(sin 4x))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−(1/2)∫(((t^2 +1)^2 )/((t−1)(t+1)(t−1−(√2))(t−1+(√2))(t+1−(√2))(t+1+(√2))))dt= =−(1/2)∫(−(1/(2(t−1)))+(1/(2(t+1)))+((√2)/(4(t−1−(√2))))−((√2)/(4(t−1+(√2))))+((√2)/(4(t+1−(√2))))−((√2)/(4(t+1+(√2)))))= [now solve with formula ∫(dt/(t+a))=ln ∣t+a∣] =((√2)/8)ln ∣((t^2 +2(√2)t+1)/(t^2 −2(√2)t+1))∣ +(1/4)ln ∣((t−1)/(t+1))∣ = =((√2)/8)ln ∣((1+(√2)sin x)/(1−(√2)sin x))∣ +(1/4)ln ∣(1/(tan ((x/2)+(π/4))))∣ +C](Q49204.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18
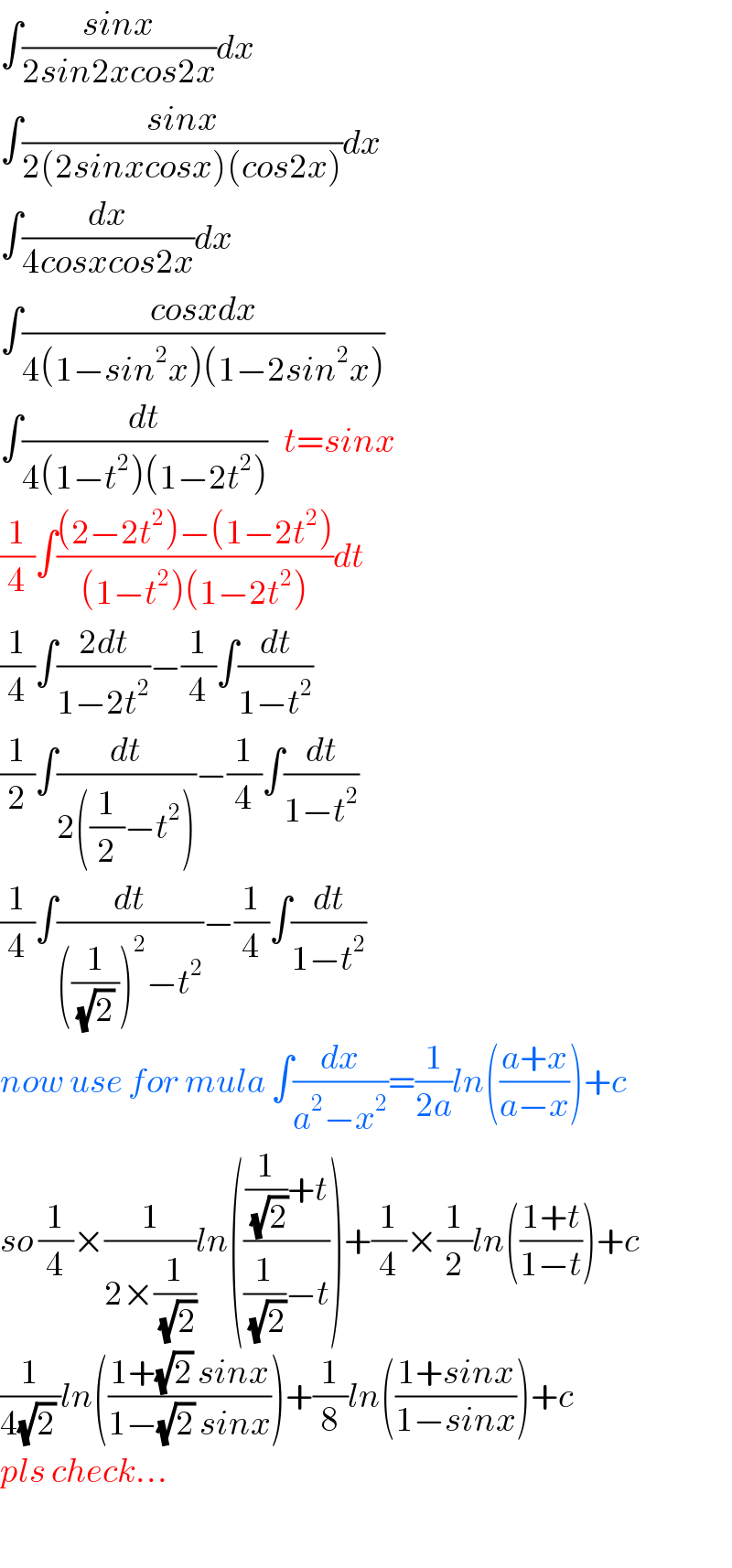
| ||
Question and Answers Forum | ||
Question Number 49187 by Rahul kharade last updated on 04/Dec/18 | ||
 | ||
Answered by MJS last updated on 04/Dec/18 | ||
![∫((sin x)/(sin 4x))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−(1/2)∫(((t^2 +1)^2 )/((t−1)(t+1)(t−1−(√2))(t−1+(√2))(t+1−(√2))(t+1+(√2))))dt= =−(1/2)∫(−(1/(2(t−1)))+(1/(2(t+1)))+((√2)/(4(t−1−(√2))))−((√2)/(4(t−1+(√2))))+((√2)/(4(t+1−(√2))))−((√2)/(4(t+1+(√2)))))= [now solve with formula ∫(dt/(t+a))=ln ∣t+a∣] =((√2)/8)ln ∣((t^2 +2(√2)t+1)/(t^2 −2(√2)t+1))∣ +(1/4)ln ∣((t−1)/(t+1))∣ = =((√2)/8)ln ∣((1+(√2)sin x)/(1−(√2)sin x))∣ +(1/4)ln ∣(1/(tan ((x/2)+(π/4))))∣ +C](Q49204.png) | ||
| ||
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18 | ||
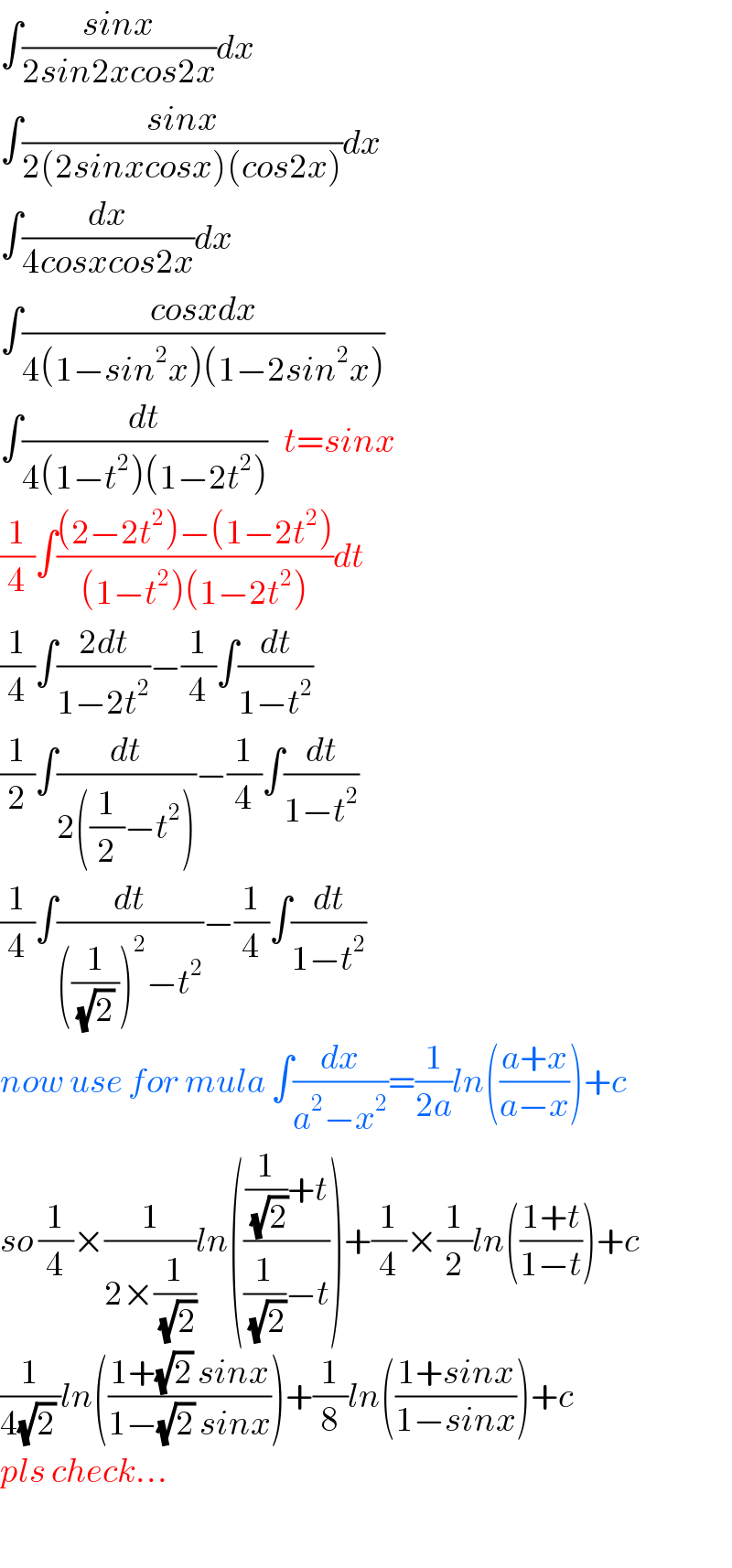 | ||
| ||