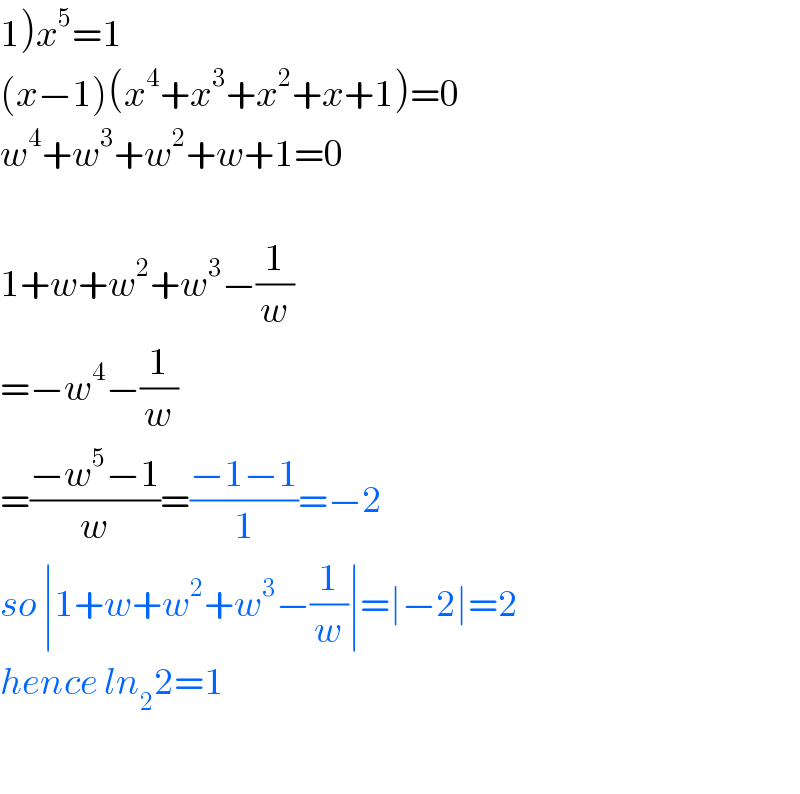Question and Answers Forum
Question Number 49202 by rahul 19 last updated on 04/Dec/18
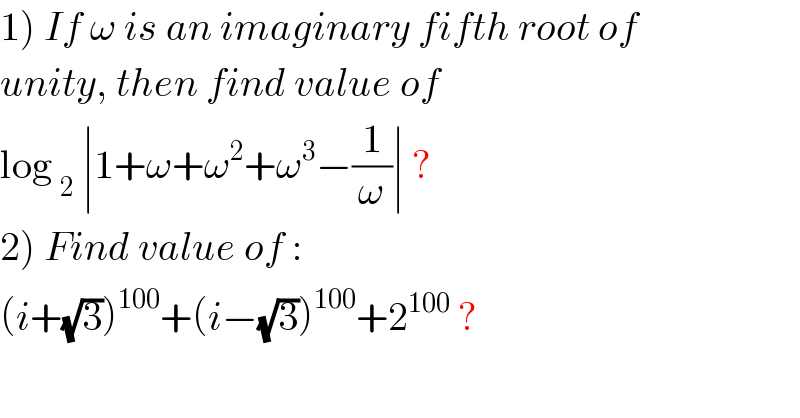
Commented by Abdo msup. last updated on 04/Dec/18
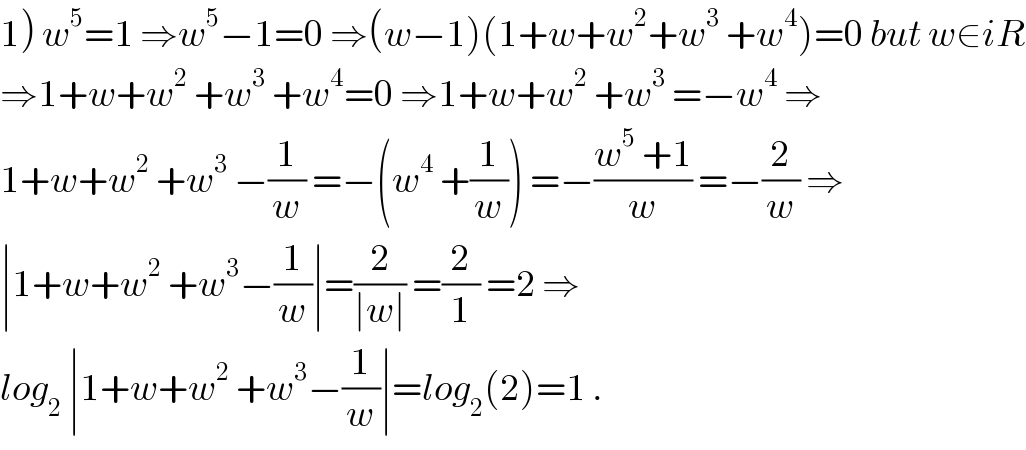
Commented by Abdo msup. last updated on 04/Dec/18

Commented by rahul 19 last updated on 05/Dec/18
thank you prof Abdo ☺️
Commented by maxmathsup by imad last updated on 05/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18

Commented by rahul 19 last updated on 05/Dec/18
thank you sir! ����
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18