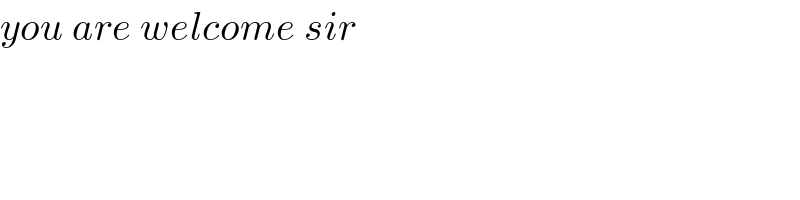Question Number 49238 by cesar.marval.larez@gmail.com last updated on 04/Dec/18
![Find the maximum common divisor of the folllwing polynomials: •f(x)=x^4 +5x^3 −4x^2 −2x and g(x)=−3x^4 −x^3 +4x^2 in Q[x]. •f(x)=2x^2 −2 and g(x)=x^4 −3x^3 +x^2 +3x−2 in R[x]](Q49238.png)
$${Find}\:{the}\:{maximum}\:{common}\:{divisor} \\ $$$${of}\:{the}\:{folllwing}\:{polynomials}: \\ $$$$\bullet{f}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}{x}\:{and}\: \\ $$$${g}\left({x}\right)=−\mathrm{3}{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} \:{in}\:{Q}\left[{x}\right]. \\ $$$$\bullet{f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}\:{and}\:{g}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\:{in}\:{R}\left[{x}\right] \\ $$
Commented by maxmathsup by imad last updated on 04/Dec/18
$${let}\:{f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}\:{and}\:{g}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \:+\mathrm{3}{x}−\mathrm{2}\:\Rightarrow \\ $$$${g}\left(\mathrm{1}\right)\:=\mathrm{1}−\mathrm{3}+\mathrm{1}+\mathrm{3}−\mathrm{2}\:=\mathrm{0}\:{and}\:{g}\left(−\mathrm{1}\right)\:=\mathrm{1}+\mathrm{3}+\mathrm{1}−\mathrm{3}−\mathrm{2}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{1}\:{divide}\:{g}\left({x}\right)\:\Rightarrow \\ $$$${g}\left({x}\right)=\lambda\left({x}^{\mathrm{2}} −\mathrm{1}\right){Q}\left({x}\right)\:{with}\:{deg}\:{Q}\:=\mathrm{2}\:\:\:{we}\:{see}\:{that}\:\lambda\:=\mathrm{1} \\ $$$$\Delta\left({f},{g}\right)\:=\Delta\left(\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right),\left({x}^{\mathrm{2}} −\mathrm{1}\right){Q}\left({x}\right)\right)\:=\left({x}^{\mathrm{2}} −\mathrm{1}\right)\Delta\left(\mathrm{2},{Q}\left({x}\right)\right)\:{but} \\ $$$${Q}\left({x}\right)={x}^{\mathrm{2}} \:+{ax}\:+{b}\:=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:+\frac{{a}}{\mathrm{2}}{x}\:+\frac{{b}}{\mathrm{2}}\right)\:=\mathrm{2}{v}\left({x}\right)\Rightarrow\Delta\left(\mathrm{2},{Q}\left({x}\right)\right) \\ $$$$=\Delta\left(\mathrm{2},\mathrm{2}{v}\left({x}\right)\right)=\mathrm{2}\Delta\left(\mathrm{1},{v}\left({x}\right)\right)=\mathrm{2}\:\Rightarrow\Delta\left({f},{g}\right)=\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${another}\:{way}\:{all}\:{roots}\:{of}\:{f}\:{are}\:{roots}\:{of}\:{g}\:\Rightarrow\:{f}\:{divide}\:{g}\:\Rightarrow\Delta\left({f},{g}\right)={f}\:. \\ $$
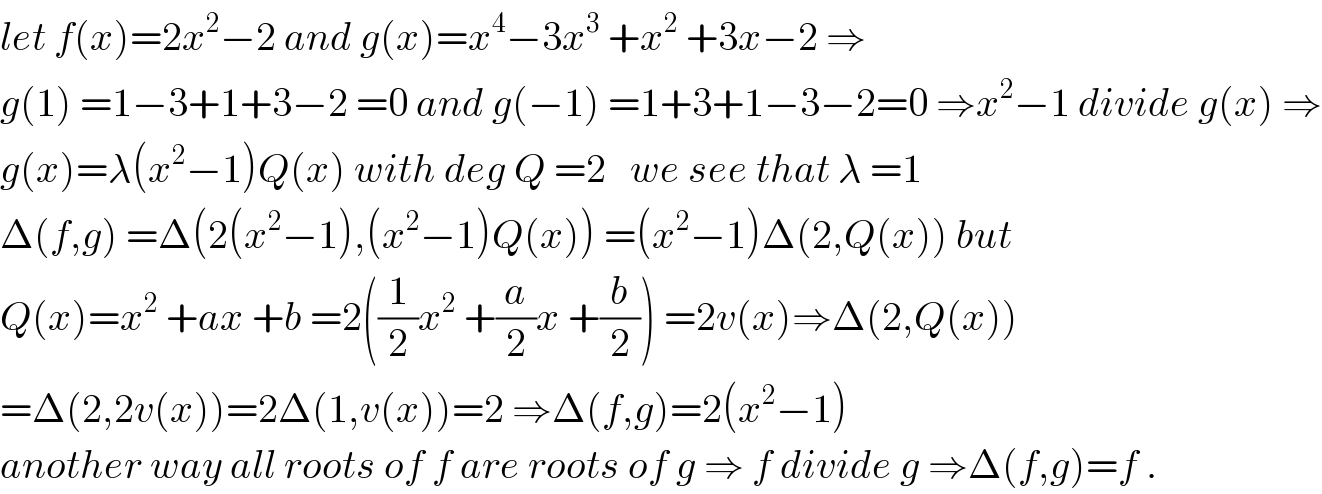
Commented by cesar.marval.larez@gmail.com last updated on 05/Dec/18
$${thank}\:{u}\:{sir} \\ $$
Commented by maxmathsup by imad last updated on 05/Dec/18
$${you}\:{are}\:{welcome}\:{sir} \\ $$