Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 49298 by peter frank last updated on 05/Dec/18

Answered by Kunal12588 last updated on 05/Dec/18

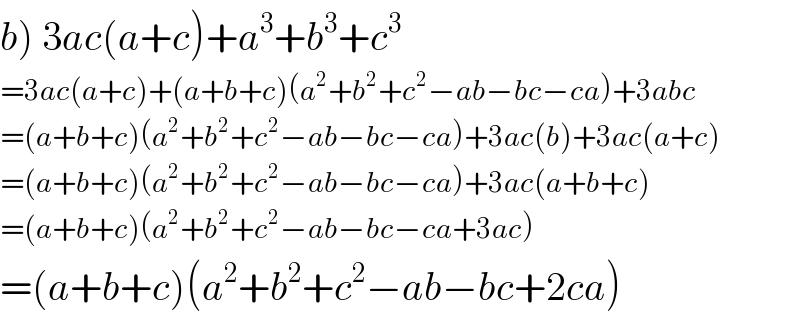
b) 3ac(a+c)+a^3 +b^3 +c^3 =3ac(a+c)+(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)+3abc =(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)+3ac(b)+3ac(a+c) =(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)+3ac(a+b+c) =(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca+3ac) =(a+b+c)(a^2 +b^2 +c^2 −ab−bc+2ca)

$$\left.{b}\right)\:\mathrm{3}{ac}\left({a}+{c}\right)+{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \\ $$$$=\mathrm{3}{ac}\left({a}+{c}\right)+\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)+\mathrm{3}{abc} \\ $$$$=\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)+\mathrm{3}{ac}\left({b}\right)+\mathrm{3}{ac}\left({a}+{c}\right) \\ $$$$=\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)+\mathrm{3}{ac}\left({a}+{b}+{c}\right) \\ $$$$=\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}+\mathrm{3}{ac}\right) \\ $$$$=\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}+\mathrm{2}{ca}\right) \\ $$

Commented by Kunal12588 last updated on 05/Dec/18

a^3 +b^3 +c^3 =(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)+3abc

$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)+\mathrm{3}{abc} \\ $$

Commented by Kunal12588 last updated on 05/Dec/18

special case when a+b+c=0 a^3 +b^3 +c^3 =3abc just reminded when I first seen this identity

$${special}\:{case} \\ $$$${when}\:{a}+{b}+{c}=\mathrm{0}\: \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc} \\ $$$${just}\:{reminded}\:{when}\:{I}\:{first}\:{seen}\:{this}\:{identity} \\ $$

Answered by Kunal12588 last updated on 05/Dec/18

(a) 27a^3 b^6 −8c^3 =(3ab^2 )^3 −(2c)^3 =(3ab^2 −2c)(9a^2 b^4 +6ab^2 +4c^2 ) as a^3 −b^3 =(a−b)(a^2 +ab+b^2 )

$$\left({a}\right)\:\mathrm{27}{a}^{\mathrm{3}} {b}^{\mathrm{6}} −\mathrm{8}{c}^{\mathrm{3}} \\ $$$$=\left(\mathrm{3}{ab}^{\mathrm{2}} \right)^{\mathrm{3}} −\left(\mathrm{2}{c}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{3}{ab}^{\mathrm{2}} −\mathrm{2}{c}\right)\left(\mathrm{9}{a}^{\mathrm{2}} {b}^{\mathrm{4}} +\mathrm{6}{ab}^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} \right) \\ $$$${as}\:{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right) \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18

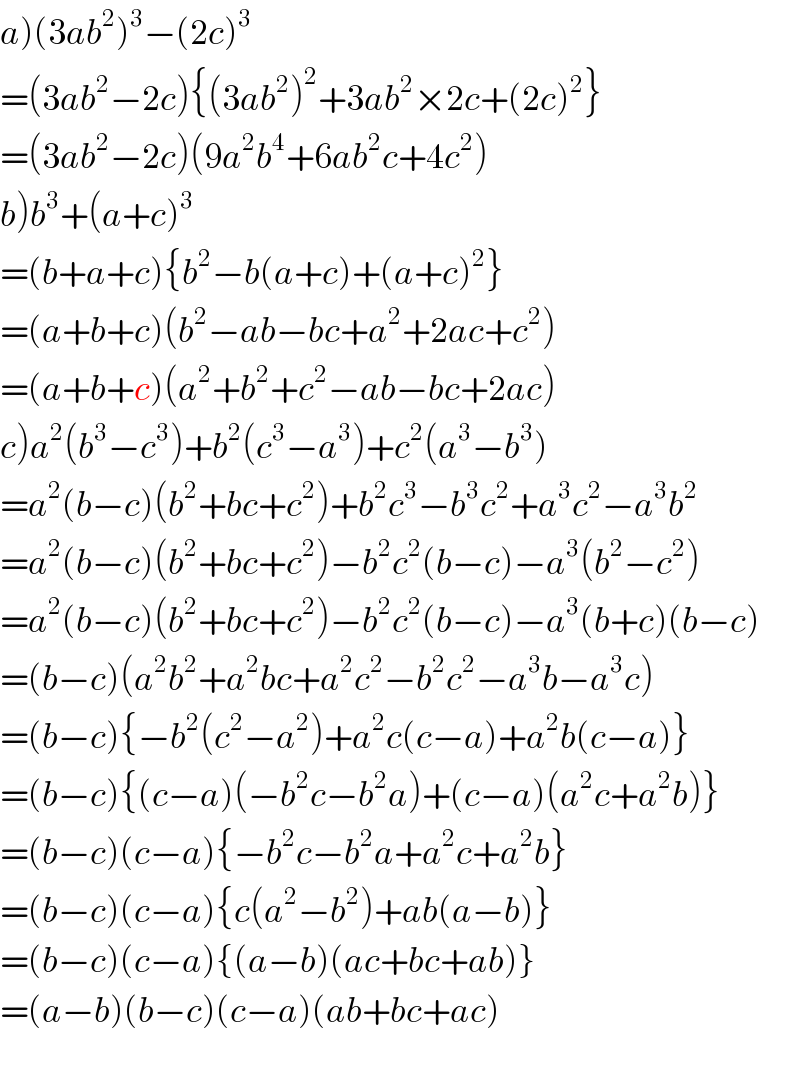
a)(3ab^2 )^3 −(2c)^3 =(3ab^2 −2c){(3ab^2 )^2 +3ab^2 ×2c+(2c)^2 } =(3ab^2 −2c)(9a^2 b^4 +6ab^2 c+4c^2 ) b)b^3 +(a+c)^3 =(b+a+c){b^2 −b(a+c)+(a+c)^2 } =(a+b+c)(b^2 −ab−bc+a^2 +2ac+c^2 ) =(a+b+c)(a^2 +b^2 +c^2 −ab−bc+2ac) c)a^2 (b^3 −c^3 )+b^2 (c^3 −a^3 )+c^2 (a^3 −b^3 ) =a^2 (b−c)(b^2 +bc+c^2 )+b^2 c^3 −b^3 c^2 +a^3 c^2 −a^3 b^2 =a^2 (b−c)(b^2 +bc+c^2 )−b^2 c^2 (b−c)−a^3 (b^2 −c^2 ) =a^2 (b−c)(b^2 +bc+c^2 )−b^2 c^2 (b−c)−a^3 (b+c)(b−c) =(b−c)(a^2 b^2 +a^2 bc+a^2 c^2 −b^2 c^2 −a^3 b−a^3 c) =(b−c){−b^2 (c^2 −a^2 )+a^2 c(c−a)+a^2 b(c−a)} =(b−c){(c−a)(−b^2 c−b^2 a)+(c−a)(a^2 c+a^2 b)} =(b−c)(c−a){−b^2 c−b^2 a+a^2 c+a^2 b} =(b−c)(c−a){c(a^2 −b^2 )+ab(a−b)} =(b−c)(c−a){(a−b)(ac+bc+ab)} =(a−b)(b−c)(c−a)(ab+bc+ac)

$$\left.{a}\right)\left(\mathrm{3}{ab}^{\mathrm{2}} \right)^{\mathrm{3}} −\left(\mathrm{2}{c}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{3}{ab}^{\mathrm{2}} −\mathrm{2}{c}\right)\left\{\left(\mathrm{3}{ab}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}{ab}^{\mathrm{2}} ×\mathrm{2}{c}+\left(\mathrm{2}{c}\right)^{\mathrm{2}} \right\} \\ $$$$=\left(\mathrm{3}{ab}^{\mathrm{2}} −\mathrm{2}{c}\right)\left(\mathrm{9}{a}^{\mathrm{2}} {b}^{\mathrm{4}} +\mathrm{6}{ab}^{\mathrm{2}} {c}+\mathrm{4}{c}^{\mathrm{2}} \right) \\ $$$$\left.{b}\right){b}^{\mathrm{3}} +\left({a}+{c}\right)^{\mathrm{3}} \\ $$$$=\left({b}+{a}+{c}\right)\left\{{b}^{\mathrm{2}} −{b}\left({a}+{c}\right)+\left({a}+{c}\right)^{\mathrm{2}} \right\} \\ $$$$=\left({a}+{b}+{c}\right)\left({b}^{\mathrm{2}} −{ab}−{bc}+{a}^{\mathrm{2}} +\mathrm{2}{ac}+{c}^{\mathrm{2}} \right) \\ $$$$=\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}+\mathrm{2}{ac}\right) \\ $$$$\left.{c}\right){a}^{\mathrm{2}} \left({b}^{\mathrm{3}} −{c}^{\mathrm{3}} \right)+{b}^{\mathrm{2}} \left({c}^{\mathrm{3}} −{a}^{\mathrm{3}} \right)+{c}^{\mathrm{2}} \left({a}^{\mathrm{3}} −{b}^{\mathrm{3}} \right) \\ $$$$={a}^{\mathrm{2}} \left({b}−{c}\right)\left({b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} \right)+{b}^{\mathrm{2}} {c}^{\mathrm{3}} −{b}^{\mathrm{3}} {c}^{\mathrm{2}} +{a}^{\mathrm{3}} {c}^{\mathrm{2}} −{a}^{\mathrm{3}} {b}^{\mathrm{2}} \\ $$$$={a}^{\mathrm{2}} \left({b}−{c}\right)\left({b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} {c}^{\mathrm{2}} \left({b}−{c}\right)−{a}^{\mathrm{3}} \left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$$$={a}^{\mathrm{2}} \left({b}−{c}\right)\left({b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} {c}^{\mathrm{2}} \left({b}−{c}\right)−{a}^{\mathrm{3}} \left({b}+{c}\right)\left({b}−{c}\right) \\ $$$$=\left({b}−{c}\right)\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {bc}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} −{a}^{\mathrm{3}} {b}−{a}^{\mathrm{3}} {c}\right) \\ $$$$=\left({b}−{c}\right)\left\{−{b}^{\mathrm{2}} \left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} {c}\left({c}−{a}\right)+{a}^{\mathrm{2}} {b}\left({c}−{a}\right)\right\} \\ $$$$=\left({b}−{c}\right)\left\{\left({c}−{a}\right)\left(−{b}^{\mathrm{2}} {c}−{b}^{\mathrm{2}} {a}\right)+\left({c}−{a}\right)\left({a}^{\mathrm{2}} {c}+{a}^{\mathrm{2}} {b}\right)\right\} \\ $$$$=\left({b}−{c}\right)\left({c}−{a}\right)\left\{−{b}^{\mathrm{2}} {c}−{b}^{\mathrm{2}} {a}+{a}^{\mathrm{2}} {c}+{a}^{\mathrm{2}} {b}\right\} \\ $$$$=\left({b}−{c}\right)\left({c}−{a}\right)\left\{{c}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+{ab}\left({a}−{b}\right)\right\} \\ $$$$=\left({b}−{c}\right)\left({c}−{a}\right)\left\{\left({a}−{b}\right)\left({ac}+{bc}+{ab}\right)\right\} \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\left({c}−{a}\right)\left({ab}+{bc}+{ac}\right) \\ $$

Commented by peter frank last updated on 06/Dec/18

thank you sir.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by $@ty@m last updated on 06/Dec/18

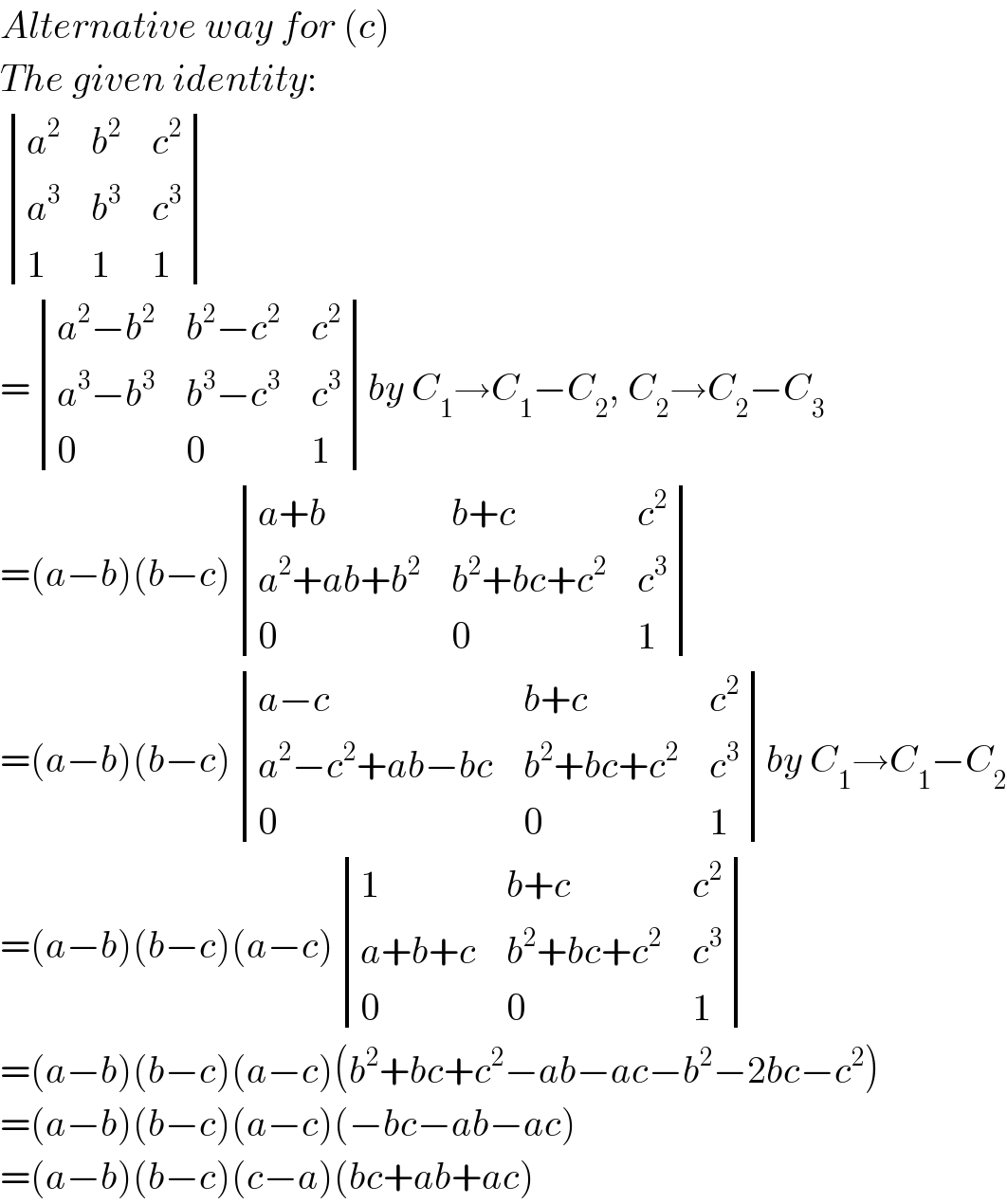
Alternative way for (c) The given identity: determinant ((a^2 ,b^2 ,c^2 ),(a^3 ,b^3 ,c^3 ),(1,1,1)) = determinant (((a^2 −b^2 ),(b^2 −c^2 ),c^2 ),((a^3 −b^3 ),(b^3 −c^3 ),c^3 ),(0,0,1))by C_1 →C_1 −C_2 , C_2 →C_2 −C_3 =(a−b)(b−c) determinant (((a+b),(b+c),c^2 ),((a^2 +ab+b^2 ),(b^2 +bc+c^2 ),c^3 ),(0,0,1)) =(a−b)(b−c) determinant (((a−c),(b+c),c^2 ),((a^2 −c^2 +ab−bc),(b^2 +bc+c^2 ),c^3 ),(0,0,1))by C_1 →C_1 −C_2 =(a−b)(b−c)(a−c) determinant ((1,(b+c),c^2 ),((a+b+c),(b^2 +bc+c^2 ),c^3 ),(0,0,1)) =(a−b)(b−c)(a−c)(b^2 +bc+c^2 −ab−ac−b^2 −2bc−c^2 ) =(a−b)(b−c)(a−c)(−bc−ab−ac) =(a−b)(b−c)(c−a)(bc+ab+ac)

$${Alternative}\:{way}\:{for}\:\left({c}\right) \\ $$$${The}\:{given}\:{identity}: \\ $$$$\begin{vmatrix}{{a}^{\mathrm{2}} }&{{b}^{\mathrm{2}} }&{{c}^{\mathrm{2}} }\\{{a}^{\mathrm{3}} }&{{b}^{\mathrm{3}} }&{{c}^{\mathrm{3}} }\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\end{vmatrix} \\ $$$$=\begin{vmatrix}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }&{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }&{{c}^{\mathrm{2}} }\\{{a}^{\mathrm{3}} −{b}^{\mathrm{3}} }&{{b}^{\mathrm{3}} −{c}^{\mathrm{3}} }&{{c}^{\mathrm{3}} }\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\end{vmatrix}{by}\:{C}_{\mathrm{1}} \rightarrow{C}_{\mathrm{1}} −{C}_{\mathrm{2}} ,\:{C}_{\mathrm{2}} \rightarrow{C}_{\mathrm{2}} −{C}_{\mathrm{3}} \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\begin{vmatrix}{{a}+{b}}&{{b}+{c}}&{{c}^{\mathrm{2}} }\\{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }&{{b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} }&{{c}^{\mathrm{3}} }\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\end{vmatrix} \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\begin{vmatrix}{{a}−{c}}&{{b}+{c}}&{{c}^{\mathrm{2}} }\\{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{ab}−{bc}}&{{b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} }&{{c}^{\mathrm{3}} }\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\end{vmatrix}{by}\:{C}_{\mathrm{1}} \rightarrow{C}_{\mathrm{1}} −{C}_{\mathrm{2}} \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\left({a}−{c}\right)\begin{vmatrix}{\mathrm{1}}&{{b}+{c}}&{{c}^{\mathrm{2}} }\\{{a}+{b}+{c}}&{{b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} }&{{c}^{\mathrm{3}} }\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\end{vmatrix} \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\left({a}−{c}\right)\left({b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} −{ab}−{ac}−{b}^{\mathrm{2}} −\mathrm{2}{bc}−{c}^{\mathrm{2}} \right) \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\left({a}−{c}\right)\left(−{bc}−{ab}−{ac}\right) \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\left({c}−{a}\right)\left({bc}+{ab}+{ac}\right) \\ $$

Commented by peter frank last updated on 06/Dec/18

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com