Question Number 49331 by rahul 19 last updated on 05/Dec/18
$${Find}\:: \\ $$$${arg}\left(\:\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}{i}\right)^{\mathrm{8}} }{\left(\mathrm{1}−{i}\right)^{\mathrm{6}} }\:\:+\:\frac{\left(\mathrm{1}+{i}\right)^{\mathrm{6}} }{\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}{i}\right)^{\mathrm{8}} }\right)\:? \\ $$
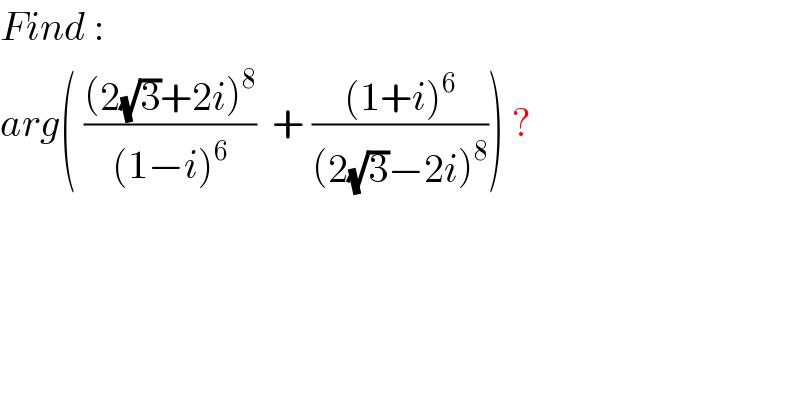
Commented by maxmathsup by imad last updated on 05/Dec/18
![let u =2(√3)+2i and v=1+i ⇒ A =(((2(√3)+2i)^8 )/((1−i)^6 )) +(((1+i)^6 )/((2(√3)−2i)^8 )) =(((u .u^− )^8 +(v.v^− )^6 )/(v^−^6 .u^−^8 )) we have ∣u∣ =2∣(√3)+i∣ =2.2=4 ⇒(u.u^− )^8 =(4^2 )^8 =4^(16) v =1+i ⇒∣v∣ =(√2) ⇒(v.v^− )^6 =2^6 ⇒A =((4^(16) +2^6 )/(u^−^8 .v^−^6 )) ⇒ arg(A)=−arg( u^−^8 .v^−^6 ) ≡−8arg(u^− )−6 arg(v^− ) [2π] but v =(√2)e^((iπ)/4) ⇒ v^− =(√2)e^(−((iπ)/4)) ⇒arg(v^− ) ≡−(π/4)[2π] also we have u =4(((√3)/2) +(i/2))=4 e^((iπ)/6) ⇒u^− =4 e^(−((iπ)/6)) ⇒arg(u^− )≡−(π/6)[2π] ⇒ arg(A)≡((8π)/6) +((6π)/4)[2π] ⇒ arg(A)≡ ((4π)/3) +((3π)/2)[2π] ⇒ arg(A)≡ ((17π)/6)[2π] but ((17π)/6) =2π +((5π)/6) ≡((5π)/6) ⇒ arg(A)≡((5π)/6)[2π] .](Q49338.png)
$${let}\:{u}\:=\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}{i}\:{and}\:{v}=\mathrm{1}+{i}\:\Rightarrow \\ $$$${A}\:=\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}{i}\right)^{\mathrm{8}} }{\left(\mathrm{1}−{i}\right)^{\mathrm{6}} }\:+\frac{\left(\mathrm{1}+{i}\right)^{\mathrm{6}} }{\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}{i}\right)^{\mathrm{8}} }\:=\frac{\left({u}\:.\overset{−} {{u}}\right)^{\mathrm{8}} \:+\left({v}.\overset{−} {{v}}\right)^{\mathrm{6}} }{\overset{−^{\mathrm{6}} } {{v}}.\overset{−^{\mathrm{8}} } {{u}}} \\ $$$${we}\:{have}\:\mid{u}\mid\:=\mathrm{2}\mid\sqrt{\mathrm{3}}+{i}\mid\:=\mathrm{2}.\mathrm{2}=\mathrm{4}\:\Rightarrow\left({u}.\overset{−} {{u}}\right)^{\mathrm{8}} \:=\left(\mathrm{4}^{\mathrm{2}} \right)^{\mathrm{8}} =\mathrm{4}^{\mathrm{16}} \\ $$$${v}\:=\mathrm{1}+{i}\:\Rightarrow\mid{v}\mid\:=\sqrt{\mathrm{2}}\:\Rightarrow\left({v}.\overset{−} {{v}}\right)^{\mathrm{6}} \:=\mathrm{2}^{\mathrm{6}} \:\Rightarrow{A}\:=\frac{\mathrm{4}^{\mathrm{16}} \:+\mathrm{2}^{\mathrm{6}} }{\overset{−^{\mathrm{8}} } {{u}}\:.\overset{−^{\mathrm{6}} } {{v}}}\:\Rightarrow \\ $$$${arg}\left({A}\right)=−{arg}\left(\:\overset{−^{\mathrm{8}} } {{u}}.\overset{−^{\mathrm{6}} } {{v}}\right)\:\equiv−\mathrm{8}{arg}\left(\overset{−} {{u}}\right)−\mathrm{6}\:{arg}\left(\overset{−} {{v}}\right)\:\left[\mathrm{2}\pi\right]\:{but} \\ $$$${v}\:=\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow\:\overset{−} {{v}}\:=\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow{arg}\left(\overset{−} {{v}}\right)\:\equiv−\frac{\pi}{\mathrm{4}}\left[\mathrm{2}\pi\right] \\ $$$${also}\:{we}\:{have}\:{u}\:=\mathrm{4}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\frac{{i}}{\mathrm{2}}\right)=\mathrm{4}\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \:\Rightarrow\overset{−} {{u}}=\mathrm{4}\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \:\Rightarrow{arg}\left(\overset{−} {{u}}\right)\equiv−\frac{\pi}{\mathrm{6}}\left[\mathrm{2}\pi\right]\:\Rightarrow \\ $$$${arg}\left({A}\right)\equiv\frac{\mathrm{8}\pi}{\mathrm{6}}\:+\frac{\mathrm{6}\pi}{\mathrm{4}}\left[\mathrm{2}\pi\right]\:\Rightarrow\:{arg}\left({A}\right)\equiv\:\frac{\mathrm{4}\pi}{\mathrm{3}}\:+\frac{\mathrm{3}\pi}{\mathrm{2}}\left[\mathrm{2}\pi\right]\:\Rightarrow\:{arg}\left({A}\right)\equiv\:\frac{\mathrm{17}\pi}{\mathrm{6}}\left[\mathrm{2}\pi\right]\:{but} \\ $$$$\frac{\mathrm{17}\pi}{\mathrm{6}}\:=\mathrm{2}\pi\:+\frac{\mathrm{5}\pi}{\mathrm{6}}\:\equiv\frac{\mathrm{5}\pi}{\mathrm{6}}\:\Rightarrow\:{arg}\left({A}\right)\equiv\frac{\mathrm{5}\pi}{\mathrm{6}}\left[\mathrm{2}\pi\right]\:. \\ $$
Commented by rahul 19 last updated on 05/Dec/18
$${I}'{m}\:{getting}\:\frac{\mathrm{5}\pi}{\mathrm{3}}\: \\ $$$${Ans}.\:{is}\:\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$${Kindly}\:{check}... \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
![a=(2(√3) +2i) a=4(((2(√3))/4)+(2/4)i)=4(cos(π/6)+isin(π/6))=4e^((iπ)/6) b=(1+i)=(√2) ((1/(√2))+i(1/(√2)))=(√2) e^((iπ)/4) {(((4e^((iπ)/6) )^8 )/(((√2) e^((−iπ)/4) )^6 ))+((((√2) e^((iπ)/4) )^6 )/((4e^((−iπ)/6) )^8 ))} ={(2^(16) /2^3 )×e^(((i4π)/3)+((i3π)/2)) +(2^3 /2^(16) )×e^(((i3π)/2)+((i4π)/3)) } =e^((i17π)/6) ×(2^(13) +2^(−13) ) now [cos(((17π)/6))+isin((17π)/6)]×(2^(13) +2^(−13) ) =[cos(2π+((5π)/6))+isin(2π+((5π)/6))]×(2^(13) +2^(−13) ) =[cos(((5π)/6))+isin(((5π)/6))]×(2^(13) +2^(−13) ) so tanθ=tan(((5π)/6)) θ=((5π)/6)](Q49336.png)
$${a}=\left(\mathrm{2}\sqrt{\mathrm{3}}\:+\mathrm{2}{i}\right) \\ $$$${a}=\mathrm{4}\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{\mathrm{2}}{\mathrm{4}}{i}\right)=\mathrm{4}\left({cos}\frac{\pi}{\mathrm{6}}+{isin}\frac{\pi}{\mathrm{6}}\right)=\mathrm{4}{e}^{\frac{{i}\pi}{\mathrm{6}}} \\ $$$${b}=\left(\mathrm{1}+{i}\right)=\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+{i}\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)=\sqrt{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \\ $$$$\left\{\frac{\left(\mathrm{4}{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)^{\mathrm{8}} }{\left(\sqrt{\mathrm{2}}\:{e}^{\frac{−{i}\pi}{\mathrm{4}}} \right)^{\mathrm{6}} }+\frac{\left(\sqrt{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{\mathrm{6}} }{\left(\mathrm{4}{e}^{\frac{−{i}\pi}{\mathrm{6}}} \right)^{\mathrm{8}} }\right\} \\ $$$$=\left\{\frac{\mathrm{2}^{\mathrm{16}} }{\mathrm{2}^{\mathrm{3}} }×{e}^{\frac{{i}\mathrm{4}\pi}{\mathrm{3}}+\frac{{i}\mathrm{3}\pi}{\mathrm{2}}} +\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{16}} }×{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{2}}+\frac{{i}\mathrm{4}\pi}{\mathrm{3}}} \right\} \\ $$$$={e}^{\frac{{i}\mathrm{17}\pi}{\mathrm{6}}} ×\left(\mathrm{2}^{\mathrm{13}} +\mathrm{2}^{−\mathrm{13}} \right) \\ $$$${now}\:\left[{cos}\left(\frac{\mathrm{17}\pi}{\mathrm{6}}\right)+{isin}\frac{\mathrm{17}\pi}{\mathrm{6}}\right]×\left(\mathrm{2}^{\mathrm{13}} +\mathrm{2}^{−\mathrm{13}} \right) \\ $$$$=\left[{cos}\left(\mathrm{2}\pi+\frac{\mathrm{5}\pi}{\mathrm{6}}\right)+{isin}\left(\mathrm{2}\pi+\frac{\mathrm{5}\pi}{\mathrm{6}}\right)\right]×\left(\mathrm{2}^{\mathrm{13}} +\mathrm{2}^{−\mathrm{13}} \right) \\ $$$$=\left[{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right)+{isin}\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right)\right]×\left(\mathrm{2}^{\mathrm{13}} +\mathrm{2}^{−\mathrm{13}} \right) \\ $$$$ \\ $$$$ \\ $$$${so}\:{tan}\theta={tan}\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right)\:\:\:\theta=\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 05/Dec/18
$${correct}\:{answer}\:{thanks}\:{sir}\:{Tanmay}. \\ $$