
Question and Answers Forum
Question Number 49605 by Rio Michael last updated on 08/Dec/18
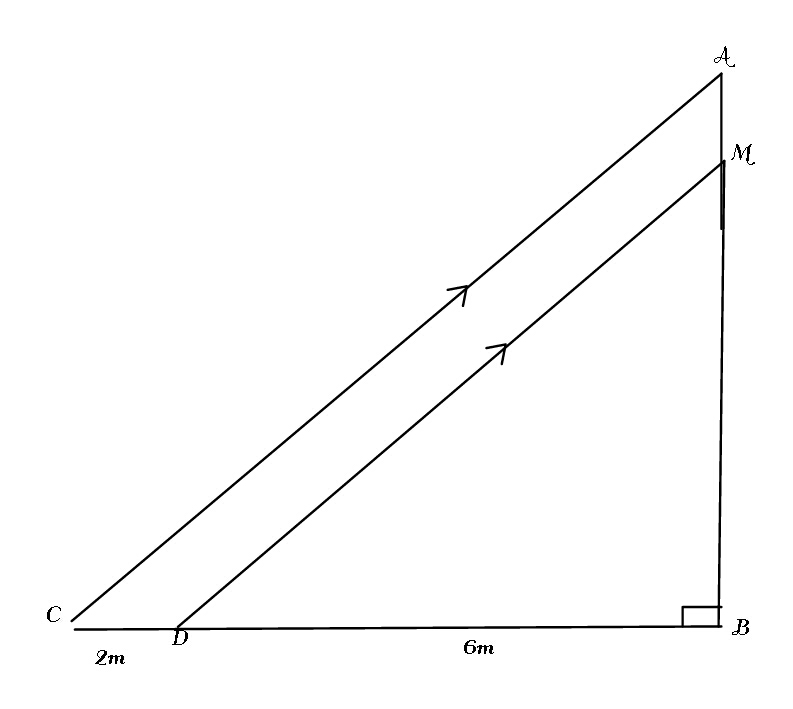
Commented by Rio Michael last updated on 08/Dec/18
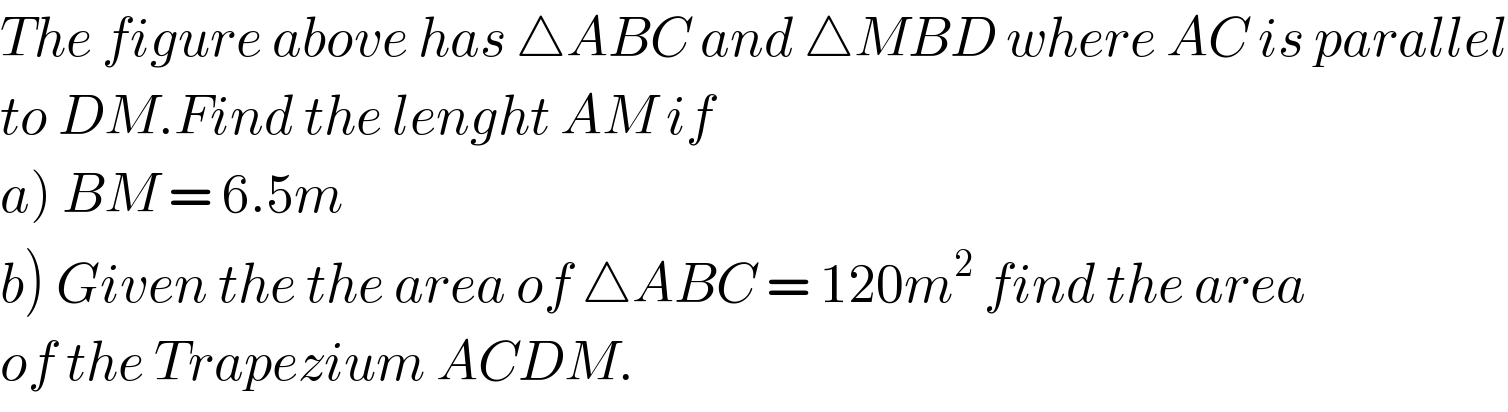
Commented by afachri last updated on 08/Dec/18

Commented by Rio Michael last updated on 08/Dec/18

Answered by Kunal12588 last updated on 08/Dec/18

Commented by Rio Michael last updated on 08/Dec/18

