Question Number 49661 by maxmathsup by imad last updated on 08/Dec/18
$${calculateA}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{i}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\left(\mathrm{1}+{ix}\right)^{{n}} −\left(\mathrm{1}−{ix}\right)^{{n}} \right\}{dx} \\ $$
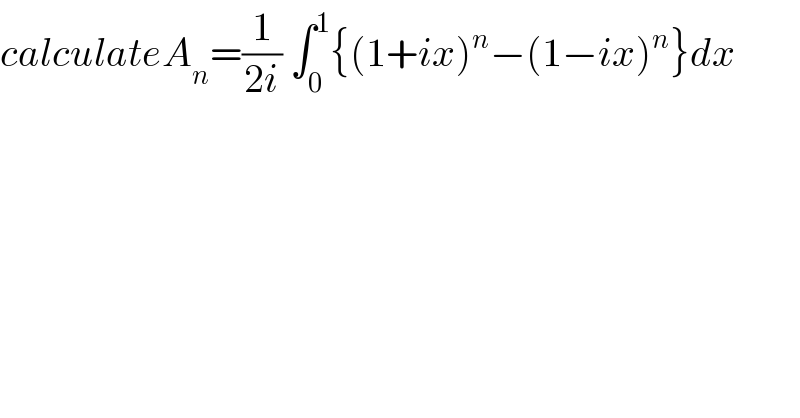
Commented by maxmathsup by imad last updated on 09/Dec/18
![we have first (1+ix)^n −(1−ix)^n =Σ_(k=0) ^n C_n ^k (ix)^k −Σ_(k=0) ^n C_n ^k (−ix)^k =Σ_(k=0) ^n C_n ^k (i^k −(−i)^k )x^k =Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) ( i^(2p+1) −(−i)^(2p+1) )x^(2p+1) =2i Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) (−1)^p x^(2p+1) ⇒ A_n =Σ_(p=0) ^([((n−1)/2)]) (−1)^p C_n ^(2p+1) ∫_0 ^1 x^(2p+1) dx =Σ_(p=0) ^([((n−1)/2)]) (−1)^p (C_n ^(2p+1) /(2p+2)) .](Q49724.png)
$${we}\:{have}\:\:{first}\:\:\left(\mathrm{1}+{ix}\right)^{{n}} −\left(\mathrm{1}−{ix}\right)^{{n}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \left({ix}\right)^{{k}} \:−\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(−{ix}\right)^{{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\left({i}^{{k}} −\left(−{i}\right)^{{k}} \right){x}^{{k}} \:=\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\left(\:{i}^{\mathrm{2}{p}+\mathrm{1}} \:−\left(−{i}\right)^{\mathrm{2}{p}+\mathrm{1}} \right){x}^{\mathrm{2}{p}+\mathrm{1}} \\ $$$$=\mathrm{2}{i}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\left(−\mathrm{1}\right)^{{p}} \:{x}^{\mathrm{2}{p}+\mathrm{1}} \:\Rightarrow \\ $$$${A}_{{n}} =\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \left(−\mathrm{1}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{p}+\mathrm{1}} \:{dx}\:=\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\left(−\mathrm{1}\right)^{{p}} \:\:\frac{{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} }{\mathrm{2}{p}+\mathrm{2}}\:. \\ $$
Commented by maxmathsup by imad last updated on 09/Dec/18
![another method we have A_n =(1/(2i))[(1/(i(n+1)))(1+ix)^(n+1) +(1/(i(n+1)))(1−ix)^(n+1) ]_0 ^1 =((−1)/(2(n+1))){ (1+i)^(n+1) +(1−i)^(n+1) −2} =((−1)/(2(n+1))){ 2Re((1+i)^(n+1) )−2} but 1+i =(√2)e^(i(π/4)) ⇒(1+i)^(n+1) =2^((n+1)/2) e^(i(n+1)(π/4)) ⇒ A_n =−(1/(n+1)){ 2^((n+1)/2) cos(n+1)(π/4) −1} =(1/(n+1)){ 1−2^((n+1)/2) cos((n+1)(π/4))} .](Q49726.png)
$${another}\:{method}\: \\ $$$${we}\:{have}\:{A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{i}}\left[\frac{\mathrm{1}}{{i}\left({n}+\mathrm{1}\right)}\left(\mathrm{1}+{ix}\right)^{{n}+\mathrm{1}} \:+\frac{\mathrm{1}}{{i}\left({n}+\mathrm{1}\right)}\left(\mathrm{1}−{ix}\right)^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left\{\:\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} \:+\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} \:−\mathrm{2}\right\} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left\{\:\mathrm{2}{Re}\left(\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} \right)−\mathrm{2}\right\}\:\:{but}\:\mathrm{1}+{i}\:=\sqrt{\mathrm{2}}{e}^{{i}\frac{\pi}{\mathrm{4}}} \:\Rightarrow\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} \:=\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} \:{e}^{{i}\left({n}+\mathrm{1}\right)\frac{\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$${A}_{{n}} =−\frac{\mathrm{1}}{{n}+\mathrm{1}}\left\{\:\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} \:{cos}\left({n}+\mathrm{1}\right)\frac{\pi}{\mathrm{4}}\:−\mathrm{1}\right\} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left\{\:\mathrm{1}−\mathrm{2}^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} \:{cos}\left(\left({n}+\mathrm{1}\right)\frac{\pi}{\mathrm{4}}\right)\right\}\:. \\ $$
Answered by Smail last updated on 09/Dec/18
![A_n =(1/(2i))[(1/(i(n+1)))(1+ix)^(n+1) −(1/(−i(n+1)))(1−ix)^(n+1) ]_0 ^1 =−(1/2)((((1+i)^(n+1) )/(n+1))+(((1−i)^(n+1) )/(n+1))−(1/(n+1))−(1/(n+1))) =−(1/(2(n+1)))(((√2))^(n+1) (e^(i(π/4)) )^(n+1) +((√2))^(n+1) (e^(−i(π/4)) )^(n+1) −2) =−(1/(2(n+1)))[((√2))^(n+1) (e^(i((π(n+1))/4)) +e^(−i((π(n+1))/4)) )−2) =−(1/((n+1)))(((√2))^(n+1) cos(((π(n+1))/4))−2)](Q49666.png)
$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{i}}\left[\frac{\mathrm{1}}{{i}\left({n}+\mathrm{1}\right)}\left(\mathrm{1}+{ix}\right)^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{−{i}\left({n}+\mathrm{1}\right)}\left(\mathrm{1}−{ix}\right)^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+\frac{\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left(\left(\sqrt{\mathrm{2}}\right)^{{n}+\mathrm{1}} \left({e}^{{i}\frac{\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} +\left(\sqrt{\mathrm{2}}\right)^{{n}+\mathrm{1}} \left({e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} −\mathrm{2}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left[\left(\sqrt{\mathrm{2}}\right)^{{n}+\mathrm{1}} \left({e}^{{i}\frac{\pi\left({n}+\mathrm{1}\right)}{\mathrm{4}}} +{e}^{−{i}\frac{\pi\left({n}+\mathrm{1}\right)}{\mathrm{4}}} \right)−\mathrm{2}\right) \\ $$$$=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\left(\left(\sqrt{\mathrm{2}}\right)^{{n}+\mathrm{1}} {cos}\left(\frac{\pi\left({n}+\mathrm{1}\right)}{\mathrm{4}}\right)−\mathrm{2}\right) \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 09/Dec/18
$${where}\:{are}\:{you}\:{from}\:{sir}\:{smail}? \\ $$
Commented by Smail last updated on 09/Dec/18
$${I}\:{am}\:{from}\:{Morocco},\:{but}\:{I}\:{live}\:{in}\:{the}\:{USA}. \\ $$
Commented by Smail last updated on 09/Dec/18
$${How}\:{about}\:{you}? \\ $$
Commented by maxmathsup by imad last updated on 09/Dec/18
$$\:{i}\:{am}\:{also}\:{morrocan}\:{theacher}\:{for}\:{the}\:{high}\:{atlas}\:\:{but}\:{i}\:{work}\:{now}\:{in}\:{casablanca}. \\ $$
Commented by Smail last updated on 09/Dec/18
$${Waw},\:{what}\:{a}\:{coincidence}. \\ $$
Commented by Smail last updated on 09/Dec/18
$${Which}\:{part}\:{of}\:{High}\:{Atlas}\:{are}\:{you}\:{from}? \\ $$
Commented by maxmathsup by imad last updated on 09/Dec/18
$${and}\:{what}\:{do}\:{you}\:{work}\:{in}\:{usa}\:{sir}\:{smail}? \\ $$
Commented by maxmathsup by imad last updated on 09/Dec/18
$$\:{a}\:{am}\:{from}\:{Azilal}\:{city}. \\ $$
Commented by Smail last updated on 09/Dec/18
$${Ana}\:{men}\:{Demnate} \\ $$
Commented by maxmathsup by imad last updated on 09/Dec/18
$${really}\:{a}\:{coincidence}\:\:{we}\:{are}\:{from}\:{the}\:{same}\:{region}\:. \\ $$
Commented by Smail last updated on 09/Dec/18
$${yup} \\ $$