Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 49830 by ajfour last updated on 11/Dec/18

Commented by ajfour last updated on 11/Dec/18

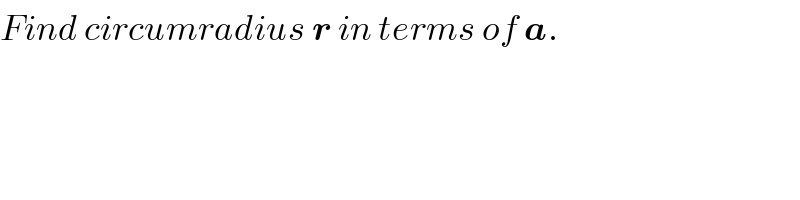
Find circumradius r in terms of a.

$${Find}\:{circumradius}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}. \\ $$

Answered by mr W last updated on 11/Dec/18

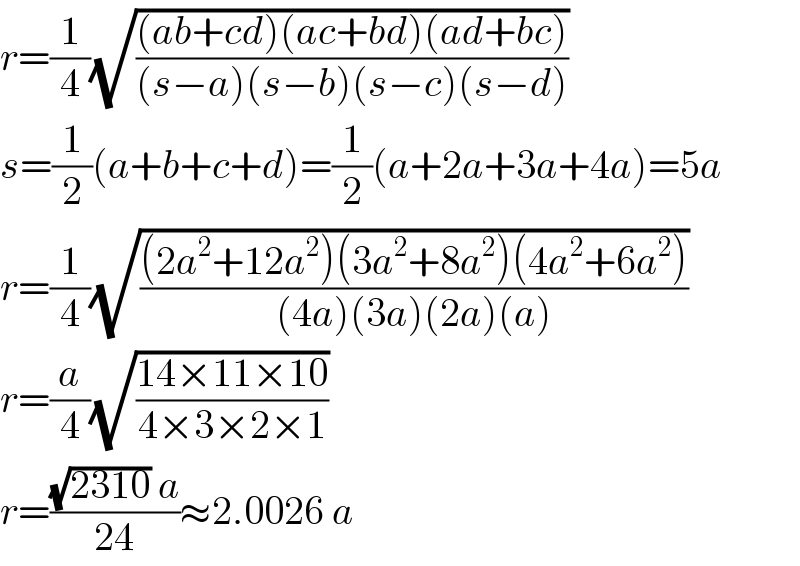
r=(1/4)(√(((ab+cd)(ac+bd)(ad+bc))/((s−a)(s−b)(s−c)(s−d)))) s=(1/2)(a+b+c+d)=(1/2)(a+2a+3a+4a)=5a r=(1/4)(√(((2a^2 +12a^2 )(3a^2 +8a^2 )(4a^2 +6a^2 ))/((4a)(3a)(2a)(a)))) r=(a/4)(√((14×11×10)/(4×3×2×1))) r=(((√(2310)) a)/(24))≈2.0026 a

$${r}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\frac{\left({ab}+{cd}\right)\left({ac}+{bd}\right)\left({ad}+{bc}\right)}{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right)}} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{b}+{c}+{d}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\mathrm{2}{a}+\mathrm{3}{a}+\mathrm{4}{a}\right)=\mathrm{5}{a} \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\frac{\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{12}{a}^{\mathrm{2}} \right)\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{8}{a}^{\mathrm{2}} \right)\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{6}{a}^{\mathrm{2}} \right)}{\left(\mathrm{4}{a}\right)\left(\mathrm{3}{a}\right)\left(\mathrm{2}{a}\right)\left({a}\right)}} \\ $$$${r}=\frac{{a}}{\mathrm{4}}\sqrt{\frac{\mathrm{14}×\mathrm{11}×\mathrm{10}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}} \\ $$$${r}=\frac{\sqrt{\mathrm{2310}}\:{a}}{\mathrm{24}}\approx\mathrm{2}.\mathrm{0026}\:{a} \\ $$

Commented by mr W last updated on 11/Dec/18

Commented by ajfour last updated on 11/Dec/18

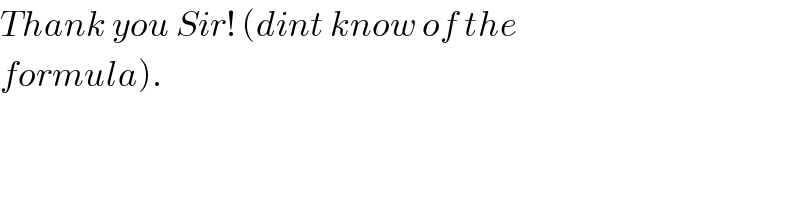
Thank you Sir! (dint know of the formula).

$${Thank}\:{you}\:{Sir}!\:\left({dint}\:{know}\:{of}\:{the}\right. \\ $$$$\left.{formula}\right). \\ $$

Answered by behi83417@gmail.com last updated on 11/Dec/18

let:(a^2 /(2r^2 ))=λ cos^(−1) ((2r^2 −a^2 )/(2r^2 ))+cos^(−1) ((2r^2 −4a^2 )/(2r^2 ))+cos^(−1) ((2r^2 −9a^2 )/(2r^2 ))+ cos^(−1) ((2r^2 −16a^2 )/(2r^2 ))=2π cos^(−1) (1−λ)+cos^(−1) (1−4λ)+cos^(−1) (1−9λ)+ +cos^(−1) (1−16λ)=2π⇒ a+b+c+d=2π⇒cos(a+c)=cos(b+d) cos^(−1) (1−λ)+cos^(−1) (1−9λ)=2π−[cos^(−1) (1−2λ)+cos^(−1) (1−16λ)] cos(a+c)=(1−λ).(1−9λ)−[(1−(1−λ)^2 ][[1−(1−9λ)^2 ]= =1−10λ−27λ^2 +180λ^3 −81λ^4 cos(b+d)=(1−4λ)(1−16λ)−[(1−(1−4λ)^2 ][(1−(1−16λ)^2 ]= =1−20λ−192λ^2 +2560λ^3 −4096λ^4 1−10λ−27λ^2 +180λ^3 −81λ^4 = 1−20λ−192λ^2 +2560λ^3 −4096λ^4 ⇒4015λ^3 −2380λ^2 +165λ+10=0 ⇒λ=(a^2 /(2r^2 ))=0.5008,0.1302⇒ ⇒(a/r)=1.007,0.5103

$${let}:\frac{{a}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }=\lambda \\ $$$${cos}^{−\mathrm{1}} \frac{\mathrm{2}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }+{cos}^{−\mathrm{1}} \frac{\mathrm{2}{r}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }+{cos}^{−\mathrm{1}} \frac{\mathrm{2}{r}^{\mathrm{2}} −\mathrm{9}{a}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }+ \\ $$$${cos}^{−\mathrm{1}} \frac{\mathrm{2}{r}^{\mathrm{2}} −\mathrm{16}{a}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }=\mathrm{2}\pi \\ $$$${cos}^{−\mathrm{1}} \left(\mathrm{1}−\lambda\right)+{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{4}\lambda\right)+{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{9}\lambda\right)+ \\ $$$$+{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{16}\lambda\right)=\mathrm{2}\pi\Rightarrow \\ $$$${a}+{b}+{c}+{d}=\mathrm{2}\pi\Rightarrow{cos}\left({a}+{c}\right)={cos}\left({b}+{d}\right) \\ $$$${cos}^{−\mathrm{1}} \left(\mathrm{1}−\lambda\right)+{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{9}\lambda\right)=\mathrm{2}\pi−\left[{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}\lambda\right)+{cos}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{16}\lambda\right)\right] \\ $$$${cos}\left({a}+{c}\right)=\left(\mathrm{1}−\lambda\right).\left(\mathrm{1}−\mathrm{9}\lambda\right)−\left[\left(\mathrm{1}−\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \right]\left[\left[\mathrm{1}−\left(\mathrm{1}−\mathrm{9}\lambda\right)^{\mathrm{2}} \right]=\right.\right. \\ $$$$=\mathrm{1}−\mathrm{10}\lambda−\mathrm{27}\lambda^{\mathrm{2}} +\mathrm{180}\lambda^{\mathrm{3}} −\mathrm{81}\lambda^{\mathrm{4}} \\ $$$${cos}\left({b}+{d}\right)=\left(\mathrm{1}−\mathrm{4}\lambda\right)\left(\mathrm{1}−\mathrm{16}\lambda\right)−\left[\left(\mathrm{1}−\left(\mathrm{1}−\mathrm{4}\lambda\right)^{\mathrm{2}} \right]\left[\left(\mathrm{1}−\left(\mathrm{1}−\mathrm{16}\lambda\right)^{\mathrm{2}} \right]=\right.\right. \\ $$$$=\mathrm{1}−\mathrm{20}\lambda−\mathrm{192}\lambda^{\mathrm{2}} +\mathrm{2560}\lambda^{\mathrm{3}} −\mathrm{4096}\lambda^{\mathrm{4}} \\ $$$$\mathrm{1}−\mathrm{10}\lambda−\mathrm{27}\lambda^{\mathrm{2}} +\mathrm{180}\lambda^{\mathrm{3}} −\mathrm{81}\lambda^{\mathrm{4}} = \\ $$$$\mathrm{1}−\mathrm{20}\lambda−\mathrm{192}\lambda^{\mathrm{2}} +\mathrm{2560}\lambda^{\mathrm{3}} −\mathrm{4096}\lambda^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{4015}\lambda^{\mathrm{3}} −\mathrm{2380}\lambda^{\mathrm{2}} +\mathrm{165}\lambda+\mathrm{10}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{a}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }=\mathrm{0}.\mathrm{5008},\mathrm{0}.\mathrm{1302}\Rightarrow\: \\ $$$$\Rightarrow\frac{{a}}{{r}}=\mathrm{1}.\mathrm{007},\mathrm{0}.\mathrm{5103} \\ $$

Answered by mr W last updated on 11/Dec/18

an other way without using formula: let α=∠A ⇒∠C=π−α let BD=l l^2 =a^2 +(4a)^2 −2(a)(4a)cos α ⇒l^2 =17a^2 −8a^2 cos α l^2 =(2a)^2 +(3a)^2 −2(2a)(3a)cos (π−α) ⇒l^2 =13a^2 +12a^2 cos α ⇒13a^2 +12a^2 cos α=17a^2 −8a^2 cos α ⇒cos α=(1/5) ⇒l^2 =17a^2 −8a^2 ×(1/5)=((77)/5)a^2 ⇒l=((√(385))/5) a r is circumradius of ΔABD with sides a, 4a, ((√(385))/5)a. r=((a×4a×((√(385))/5)a)/(√((a+4a+((√(385))/5)a)(−a+4a+((√(385))/5)a)(a−4a+((√(385))/5)a)(a+4a−((√(385))/5)a)))) r=((4×((√(385))/5)a)/(√((((385)/(25))−9)(25−((385)/(25))))))=((20(√(385))a)/(√(160×240))) r=(((√(385))a)/(4(√6)))=(((√(2310)) a)/(24))≈2.0026 a

$${an}\:{other}\:{way}\:{without}\:{using}\:{formula}: \\ $$$${let}\:\alpha=\angle{A} \\ $$$$\Rightarrow\angle{C}=\pi−\alpha \\ $$$${let}\:{BD}={l} \\ $$$${l}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\mathrm{4}{a}\right)^{\mathrm{2}} −\mathrm{2}\left({a}\right)\left(\mathrm{4}{a}\right)\mathrm{cos}\:\alpha \\ $$$$\Rightarrow{l}^{\mathrm{2}} =\mathrm{17}{a}^{\mathrm{2}} −\mathrm{8}{a}^{\mathrm{2}} \:\mathrm{cos}\:\alpha \\ $$$${l}^{\mathrm{2}} =\left(\mathrm{2}{a}\right)^{\mathrm{2}} +\left(\mathrm{3}{a}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}{a}\right)\left(\mathrm{3}{a}\right)\mathrm{cos}\:\left(\pi−\alpha\right) \\ $$$$\Rightarrow{l}^{\mathrm{2}} =\mathrm{13}{a}^{\mathrm{2}} +\mathrm{12}{a}^{\mathrm{2}} \:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\mathrm{13}{a}^{\mathrm{2}} +\mathrm{12}{a}^{\mathrm{2}} \:\mathrm{cos}\:\alpha=\mathrm{17}{a}^{\mathrm{2}} −\mathrm{8}{a}^{\mathrm{2}} \:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow{l}^{\mathrm{2}} =\mathrm{17}{a}^{\mathrm{2}} −\mathrm{8}{a}^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{77}}{\mathrm{5}}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{l}=\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}\:{a} \\ $$$${r}\:{is}\:{circumradius}\:{of}\:\Delta{ABD}\:{with}\:{sides} \\ $$$${a},\:\mathrm{4}{a},\:\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}. \\ $$$${r}=\frac{{a}×\mathrm{4}{a}×\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}}{\sqrt{\left({a}+\mathrm{4}{a}+\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}\right)\left(−{a}+\mathrm{4}{a}+\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}\right)\left({a}−\mathrm{4}{a}+\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}\right)\left({a}+\mathrm{4}{a}−\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}\right)}} \\ $$$${r}=\frac{\mathrm{4}×\frac{\sqrt{\mathrm{385}}}{\mathrm{5}}{a}}{\sqrt{\left(\frac{\mathrm{385}}{\mathrm{25}}−\mathrm{9}\right)\left(\mathrm{25}−\frac{\mathrm{385}}{\mathrm{25}}\right)}}=\frac{\mathrm{20}\sqrt{\mathrm{385}}{a}}{\sqrt{\mathrm{160}×\mathrm{240}}} \\ $$$${r}=\frac{\sqrt{\mathrm{385}}{a}}{\mathrm{4}\sqrt{\mathrm{6}}}=\frac{\sqrt{\mathrm{2310}}\:{a}}{\mathrm{24}}\approx\mathrm{2}.\mathrm{0026}\:{a} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com