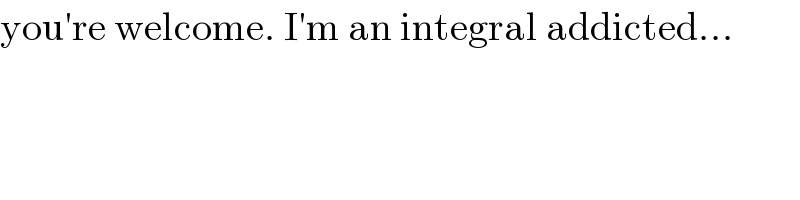∫(dx/(√((a+1)cos 2x +4cos x −a+3)))=?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 49838 by MJS last updated on 11/Dec/18

$\int \frac{d x}{\sqrt{(a + 1) \cos 2 x + 4 \cos x - a + 3}} = ?$
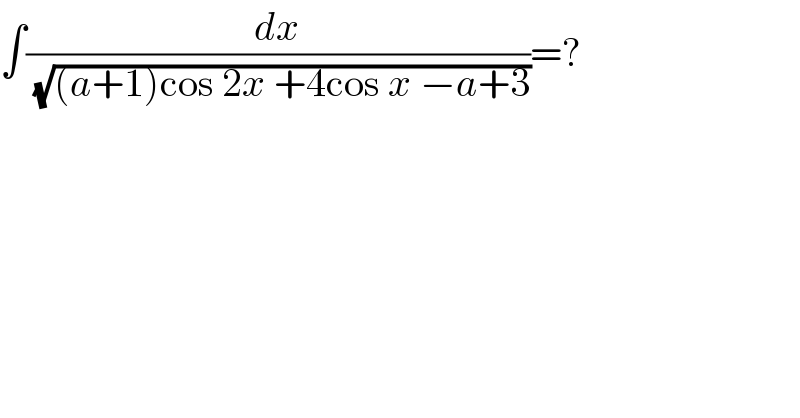
Commented by MJS last updated on 11/Dec/18

$\int \frac{d x}{\sqrt{(a + 1) \cos 2 x + 4 \cos x - a + 3}} =$ $[t = \frac{x}{2} \to d x = 2 d t]$ $= 2 \int \frac{d t}{\sqrt{(a + 1) \cos 4 t + 4 \cos 2 t - a + 3}} =$ $= \frac{\sqrt{2}}{2} \int \frac{d t}{\cos t \sqrt{(a + 1) \cos^{2} t - a}} =$ $[u = \tan t \to d t = \frac{d u}{u^{2} + 1}; \cos t = \frac{1}{\sqrt{u^{2} + 1}}]$ $= \frac{\sqrt{2}}{2} \int \frac{d u}{\sqrt{1 - {a u}^{2}}} =$ $[v = \sqrt{a} u \to d u = \frac{d v}{\sqrt{a}}]$ $= \frac{1}{\sqrt{2 a}} \int \frac{d v}{\sqrt{1 - v^{2}}} = \frac{1}{\sqrt{2 a}} \arcsin v = \frac{1}{\sqrt{2 a}} \arcsin (\sqrt{a} u) =$ $= \frac{1}{\sqrt{2 a}} \arcsin (\sqrt{a} \tan t) = \frac{1}{\sqrt{2 a}} \arcsin (\sqrt{a} \tan \frac{x}{2}) + C$
	Answered by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18
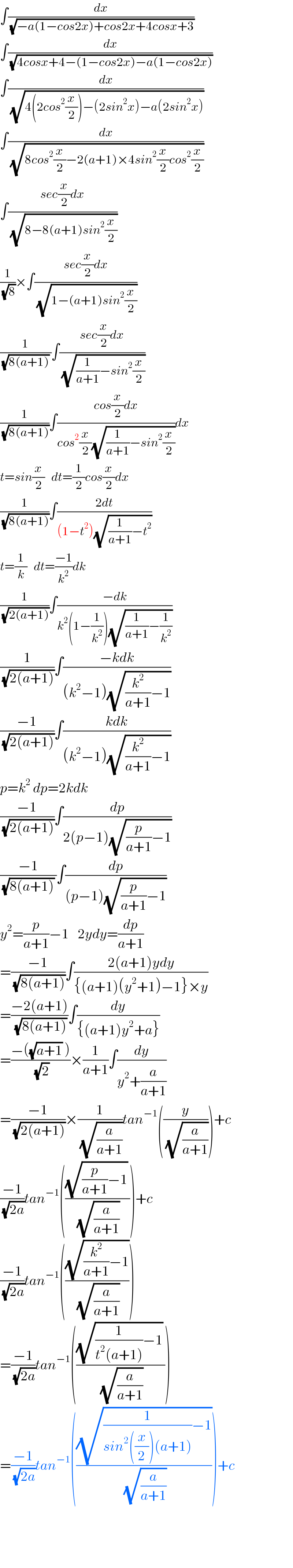
	$∫(dx/(√(−a(1−cos2x)+cos2x+4cosx+3))) ∫(dx/(√(4cosx+4−(1−cos2x)−a(1−cos2x)))) ∫(dx/(√(4(2cos^2 (x/2))−(2sin^2 x)−a(2sin^2 x)))) ∫(dx/(√(8cos^2 (x/2)−2(a+1)×4sin^2 (x/2)cos^2 (x/2)))) ∫((sec(x/2)dx)/(√(8−8(a+1)sin^2 (x/2)))) (1/(√8))×∫((sec(x/2)dx)/(√(1−(a+1)sin^2 (x/2)))) (1/((√(8(a+1))) ))∫((sec(x/2)dx)/(√((1/(a+1))−sin^2 (x/2)))) (1/(√(8(a+1))))∫((cos(x/2)dx)/(cos^2 (x/2)(√((1/(a+1))−sin^2 (x/2)))))dx t=sin(x/2) dt=(1/2)cos(x/2)dx (1/(√(8(a+1))))∫((2dt)/((1−t^2 )(√((1/(a+1))−t^2 )))) t=(1/k) dt=((−1)/k^2 )dk (1/(√(2(a+1))))∫((−dk)/(k^2 (1−(1/k^2 ))(√((1/(a+1))−(1/k^2 ))))) (1/(√(2(a+1))))∫((−kdk)/((k^2 −1)(√((k^2 /(a+1))−1)))) ((−1)/(√(2(a+1))))∫((kdk)/((k^2 −1)(√((k^2 /(a+1))−1)))) p=k^2 dp=2kdk ((−1)/(√(2(a+1))))∫(dp/(2(p−1)(√((p/(a+1))−1)))) ((−1)/((√(8(a+1))) ))∫(dp/((p−1)(√((p/(a+1))−1)))) y^2 =(p/(a+1))−1 2ydy=(dp/(a+1)) =((−1)/(√(8(a+1))))∫((2(a+1)ydy)/({(a+1)(y^2 +1)−1}×y)) =((−2(a+1))/(√(8(a+1))))∫(dy/({(a+1)y^2 +a})) =((−((√(a+1)) ))/(√2))×(1/(a+1))∫(dy/(y^2 +(a/(a+1)))) =((−1)/(√(2(a+1))))×(1/(√(a/(a+1))))tan^(−1) ((y/(√(a/(a+1)))))+c ((−1)/(√(2a)))tan^(−1) ((((√((p/(a+1))−1)) )/(√(a/(a+1)))))+c ((−1)/(√(2a)))tan^(−1) (((√((k^2 /(a+1))−1))/(√(a/(a+1))))) =((−1)/(√(2a)))tan^(−1) ((((√((1/(t^2 (a+1)))−1)) )/(√(a/(a+1))))) =((−1)/(√(2a)))tan^(−1) (((√((1/(sin^2 ((x/2))(a+1)))−1))/(√(a/(a+1)))))+c$
	$\int \frac{d x}{\sqrt{- a (1 - c o s 2 x) + c o s 2 x + 4 c o s x + 3}}$ $\int \frac{d x}{\sqrt{4 c o s x + 4 - (1 - c o s 2 x) - a (1 - c o s 2 x)}}$ $\int \frac{d x}{\sqrt{4 (2 {c o s}^{2} \frac{x}{2}) - (2 {s i n}^{2} x) - a (2 {s i n}^{2} x)}}$ $\int \frac{d x}{\sqrt{8 {c o s}^{2} \frac{x}{2} - 2 (a + 1) \times 4 {s i n}^{2} \frac{x}{2} {c o s}^{2} \frac{x}{2}}}$ $\int \frac{s e c \frac{x}{2} d x}{\sqrt{8 - 8 (a + 1) {s i n}^{2} \frac{x}{2}}}$ $\frac{1}{\sqrt{8}} \times \int \frac{s e c \frac{x}{2} d x}{\sqrt{1 - (a + 1) {s i n}^{2} \frac{x}{2}}}$ $\frac{1}{\sqrt{8 (a + 1)}} \int \frac{s e c \frac{x}{2} d x}{\sqrt{\frac{1}{a + 1} - {s i n}^{2} \frac{x}{2}}}$ $\frac{1}{\sqrt{8 (a + 1)}} \int \frac{c o s \frac{x}{2} d x}{{c o s}^{2} \frac{x}{2} \sqrt{\frac{1}{a + 1} - {s i n}^{2} \frac{x}{2}}} d x$ $t = s i n \frac{x}{2} d t = \frac{1}{2} c o s \frac{x}{2} d x$ $\frac{1}{\sqrt{8 (a + 1)}} \int \frac{2 d t}{(1 - t^{2}) \sqrt{\frac{1}{a + 1} - t^{2}}}$ $t = \frac{1}{k} d t = \frac{- 1}{k^{2}} d k$ $\frac{1}{\sqrt{2 (a + 1)}} \int \frac{- d k}{k^{2} (1 - \frac{1}{k^{2}}) \sqrt{\frac{1}{a + 1} - \frac{1}{k^{2}}}}$ $\frac{1}{\sqrt{2 (a + 1)}} \int \frac{- k d k}{(k^{2} - 1) \sqrt{\frac{k^{2}}{a + 1} - 1}}$ $\frac{- 1}{\sqrt{2 (a + 1)}} \int \frac{k d k}{(k^{2} - 1) \sqrt{\frac{k^{2}}{a + 1} - 1}}$ $p = k^{2} d p = 2 k d k$ $\frac{- 1}{\sqrt{2 (a + 1)}} \int \frac{d p}{2 (p - 1) \sqrt{\frac{p}{a + 1} - 1}}$ $\frac{- 1}{\sqrt{8 (a + 1)}} \int \frac{d p}{(p - 1) \sqrt{\frac{p}{a + 1} - 1}}$ $y^{2} = \frac{p}{a + 1} - 1 2 y d y = \frac{d p}{a + 1}$ $= \frac{- 1}{\sqrt{8 (a + 1)}} \int \frac{2 (a + 1) y d y}{{(a + 1) (y^{2} + 1) - 1} \times y}$ $= \frac{- 2 (a + 1)}{\sqrt{8 (a + 1)}} \int \frac{d y}{{(a + 1) y^{2} + a}}$ $= \frac{- (\sqrt{a + 1})}{\sqrt{2}} \times \frac{1}{a + 1} \int \frac{d y}{y^{2} + \frac{a}{a + 1}}$ $= \frac{- 1}{\sqrt{2 (a + 1)}} \times \frac{1}{\sqrt{\frac{a}{a + 1}}} {t a n}^{- 1} (\frac{y}{\sqrt{\frac{a}{a + 1}}}) + c$ $\frac{- 1}{\sqrt{2 a}} {t a n}^{- 1} (\frac{\sqrt{\frac{p}{a + 1} - 1}}{\sqrt{\frac{a}{a + 1}}}) + c$ $\frac{- 1}{\sqrt{2 a}} {t a n}^{- 1} (\frac{\sqrt{\frac{k^{2}}{a + 1} - 1}}{\sqrt{\frac{a}{a + 1}}})$ $= \frac{- 1}{\sqrt{2 a}} {t a n}^{- 1} (\frac{\sqrt{\frac{1}{t^{2} (a + 1)} - 1}}{\sqrt{\frac{a}{a + 1}}})$ $= \frac{- 1}{\sqrt{2 a}} {t a n}^{- 1} (\frac{\sqrt{\frac{1}{{s i n}^{2} (\frac{x}{2}) (a + 1)} - 1}}{\sqrt{\frac{a}{a + 1}}}) + c$
	Commented by MJS last updated on 11/Dec/18

	$correct, thank you!$
	Commented by malwaan last updated on 12/Dec/18

	$great$ $thank you$
	Commented by tanmay.chaudhury50@gmail.com last updated on 12/Dec/18

	$M J S s i r y o u r m e t h o d i s s h o r t a n d t r i c k y,$ $t h a n k y o u s i r . . .$
	Commented by MJS last updated on 12/Dec/18

	${you}^{'} re welcome . I^{'} m an integral addicted . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum