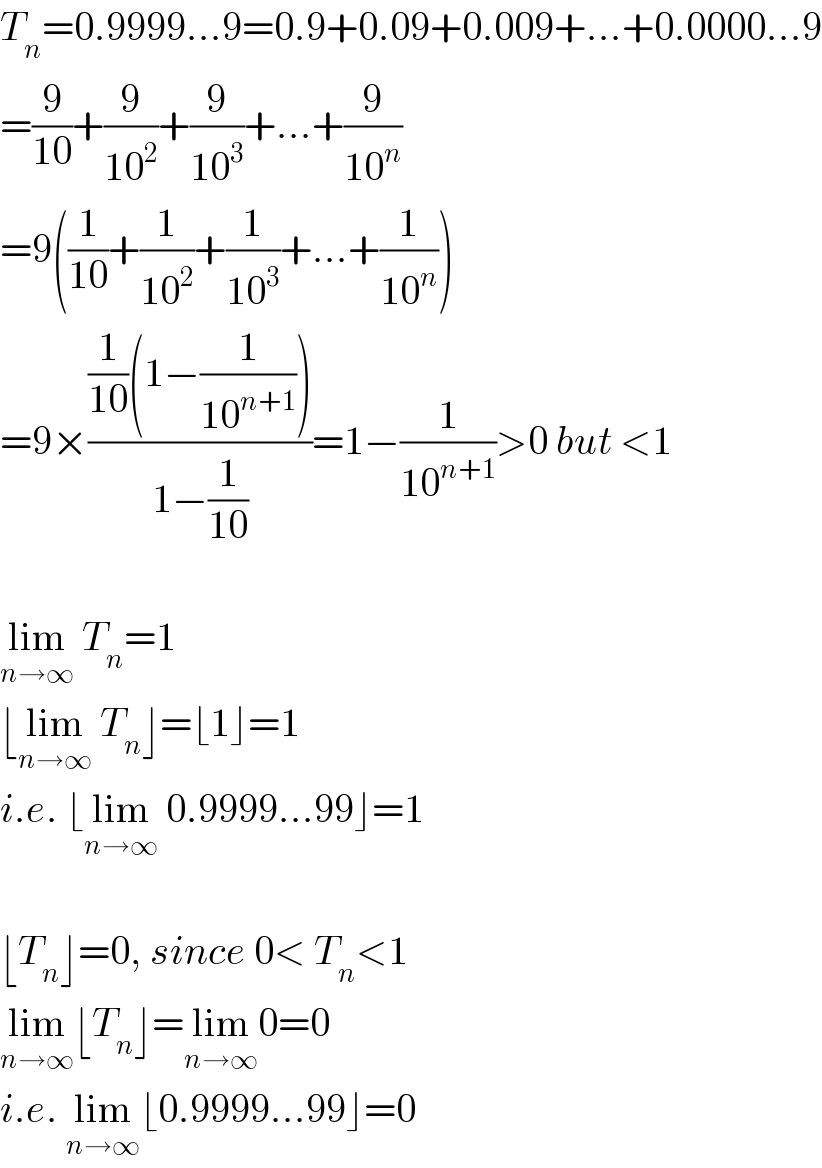Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 49859 by hassentimol last updated on 11/Dec/18

Commented by hassentimol last updated on 11/Dec/18

Could someone please explain me why this ? I know that 0.999...=1 is true but why the above shown is correct ? I don′t undersand it...

$$\mathrm{Could}\:\mathrm{someone}\:\mathrm{please}\:\mathrm{explain}\:\mathrm{me}\:\mathrm{why}\:\mathrm{this}\:? \\ $$$$\mathrm{I}\:\mathrm{know}\:\mathrm{that}\:\mathrm{0}.\mathrm{999}...=\mathrm{1}\:\mathrm{is}\:\mathrm{true}\:\mathrm{but}\:\mathrm{why}\:\mathrm{the} \\ $$$$\mathrm{above}\:\mathrm{shown}\:\mathrm{is}\:\mathrm{correct}\:?\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{undersand}\:\mathrm{it}... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18

Commented by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18

Commented by maxmathsup by imad last updated on 11/Dec/18

we have 0,99..=0,9 +0,09 +..=(9/(10)) +(9/(100)) +(9/(1000)) +... =(9/(10))( 1 +(1/(10)) +(1/(100)) +...) =(9/(10))( 1+(1/(10)) +((1/(10)))^2 +...) =(9/(10)) .(1/(1−(1/(10)))) =1 ⇒ lim_(n→+∞) 0,999....9( with n 9)=1 ⇒[lim_(n→+∞) ]=1 but ∀n ∈N 0,999..(n 9) <1 ⇒[0,9999(n 9]=0 ⇒lim_(n→+∞) [....]=0

$${we}\:{have}\:\mathrm{0},\mathrm{99}..=\mathrm{0},\mathrm{9}\:+\mathrm{0},\mathrm{09}\:+..=\frac{\mathrm{9}}{\mathrm{10}}\:+\frac{\mathrm{9}}{\mathrm{100}}\:+\frac{\mathrm{9}}{\mathrm{1000}}\:+... \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}\left(\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{10}}\:+\frac{\mathrm{1}}{\mathrm{100}}\:+...\right)\:=\frac{\mathrm{9}}{\mathrm{10}}\left(\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}\:+\left(\frac{\mathrm{1}}{\mathrm{10}}\right)^{\mathrm{2}} \:+...\right)\:=\frac{\mathrm{9}}{\mathrm{10}}\:.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}\:=\mathrm{1}\:\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \mathrm{0},\mathrm{999}....\mathrm{9}\left(\:{with}\:{n}\:\mathrm{9}\right)=\mathrm{1}\:\Rightarrow\left[{lim}_{{n}\rightarrow+\infty} \right]=\mathrm{1} \\ $$$${but}\:\forall{n}\:\in{N}\:\:\:\mathrm{0},\mathrm{999}..\left({n}\:\mathrm{9}\right)\:<\mathrm{1}\:\Rightarrow\left[\mathrm{0},\mathrm{9999}\left({n}\:\mathrm{9}\right]=\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \left[....\right]=\mathrm{0}\right. \\ $$

Answered by MJS last updated on 11/Dec/18

the ⌊ ⌋ make the difference ⌊x⌋ is the greatest integer ≤x ⌊lim_(n→∞) f(n)⌋ calculates the limit first. in our case the limit is 1, and ⌊1⌋=1 lim_(n→∞) ⌊f(n)⌋ calculates the limit of the greatest integer, ⌊0.9999...⌋=0, no matter how many 9s you add

$$\mathrm{the}\:\lfloor\:\rfloor\:\mathrm{make}\:\mathrm{the}\:\mathrm{difference} \\ $$$$\lfloor{x}\rfloor\:\mathrm{is}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{integer}\:\leqslant{x} \\ $$$$\lfloor\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({n}\right)\rfloor\:\mathrm{calculates}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{first}.\:\mathrm{in}\:\mathrm{our} \\ $$$$\mathrm{case}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{1},\:\mathrm{and}\:\lfloor\mathrm{1}\rfloor=\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor{f}\left({n}\right)\rfloor\:\mathrm{calculates}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{greatest} \\ $$$$\mathrm{integer},\:\lfloor\mathrm{0}.\mathrm{9999}...\rfloor=\mathrm{0},\:\mathrm{no}\:\mathrm{matter}\:\mathrm{how}\:\mathrm{many} \\ $$$$\mathrm{9s}\:\mathrm{you}\:\mathrm{add} \\ $$

Answered by mr W last updated on 11/Dec/18

T_n =0.9999...9=0.9+0.09+0.009+...+0.0000...9 =(9/(10))+(9/(10^2 ))+(9/(10^3 ))+...+(9/(10^n )) =9((1/(10))+(1/(10^2 ))+(1/(10^3 ))+...+(1/(10^n ))) =9×(((1/(10))(1−(1/(10^(n+1) ))))/(1−(1/(10))))=1−(1/(10^(n+1) ))>0 but <1 lim_(n→∞) T_n =1 ⌊lim_(n→∞) T_n ⌋=⌊1⌋=1 i.e. ⌊lim_(n→∞) 0.9999...99⌋=1 ⌊T_n ⌋=0, since 0< T_n <1 lim_(n→∞) ⌊T_n ⌋=lim_(n→∞) 0=0 i.e. lim_(n→∞) ⌊0.9999...99⌋=0

$${T}_{{n}} =\mathrm{0}.\mathrm{9999}...\mathrm{9}=\mathrm{0}.\mathrm{9}+\mathrm{0}.\mathrm{09}+\mathrm{0}.\mathrm{009}+...+\mathrm{0}.\mathrm{0000}...\mathrm{9} \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}+\frac{\mathrm{9}}{\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{10}^{\mathrm{3}} }+...+\frac{\mathrm{9}}{\mathrm{10}^{{n}} } \\ $$$$=\mathrm{9}\left(\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{3}} }+...+\frac{\mathrm{1}}{\mathrm{10}^{{n}} }\right) \\ $$$$=\mathrm{9}×\frac{\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{{n}+\mathrm{1}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{{n}+\mathrm{1}} }>\mathrm{0}\:{but}\:<\mathrm{1} \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{T}_{{n}} =\mathrm{1} \\ $$$$\lfloor\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{T}_{{n}} \rfloor=\lfloor\mathrm{1}\rfloor=\mathrm{1} \\ $$$${i}.{e}.\:\lfloor\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{0}.\mathrm{9999}...\mathrm{99}\rfloor=\mathrm{1} \\ $$$$ \\ $$$$\lfloor{T}_{{n}} \rfloor=\mathrm{0},\:{since}\:\mathrm{0}<\:{T}_{{n}} <\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor{T}_{{n}} \rfloor=\underset{{n}\rightarrow\infty} {\mathrm{lim}0}=\mathrm{0} \\ $$$${i}.{e}.\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor\mathrm{0}.\mathrm{9999}...\mathrm{99}\rfloor=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com