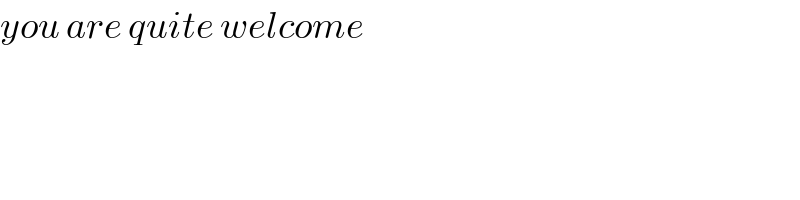find ∫_0 ^1 cos(n arcosx)dx with n integr natural.


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 49956 by maxmathsup by imad last updated on 12/Dec/18

$f i n d \int_{0}^{1} c o s (n a r c o s x) d x w i t h n i n t e g r n a t u r a l .$
Commented by Abdo msup. last updated on 13/Dec/18

$w e h a v e c o s (n a r c o s x) + i s i n (n a r c o s x)$ $= {(c o s (a r c o s x) + i s i n (a r c o s x))}^{n}$ $= {(x + i \sqrt{1 - x^{2}})}^{n} a n d \int_{0}^{1} c o s (n a r c o s x) d x$ $= R e (\int_{0}^{1} {(x + i \sqrt{1 - x^{2}})}^{n} d x) b u t$ ${(x + i \sqrt{1 - x^{2}})}^{n} = \sum_{k = 0}^{n} C_{n}^{k} {(i \sqrt{1 - x^{2}})}^{k} x^{n - k}$ $= \sum_{k = 0}^{n} i^{k} C_{n}^{k} {(1 - x^{2})}^{\frac{k}{2}} x^{n - k}$ $= \sum_{p = 0}^{[\frac{n}{2}]} {(- 1)}^{p} C_{n}^{2 p} {(1 - x^{2})}^{p} x^{n - 2 p}$ $+ \sum_{p = 0}^{[\frac{n - 1}{2}]} i {(- 1)}^{p} C_{n}^{2 p + 1} {(1 - x^{2})}^{\frac{2 p + 1}{2}} x^{n - 2 p - 1} \Rightarrow$ $\int_{0}^{1} c o s (n a r c o s x) d x = (\int_{0}^{1} \sum_{p = 0}^{[\frac{n}{2}]} {(- 1)}^{p} C_{n}^{2 p} {(1 - x^{2})}^{p} x^{n - 2 p} d x)$ $= \sum_{p = 0}^{[\frac{n}{2}]} {(- 1)}^{p} C_{n}^{2 p} \int_{0}^{1} {(1 - x^{2})}^{p} x^{n - 2 p} d x c h a n g e m e n t$ $x = s i n t g i v e$ $\int_{0}^{1} {(1 - x^{2})}^{p} x^{n - 2 p} d x = \int_{0}^{\frac{π}{2}} {c o s}^{2 p} t {s i n}^{n - 2 p} t c o s t d t$ $= \int_{0}^{\frac{π}{2}} {c o s}^{2 p + 1} t {s i n}^{n - 2 p} t d t . . . b e c o n t i n u e d . . .$
	Answered by Smail last updated on 13/Dec/18

	$t = a r c o s (x) \Rightarrow d t = \frac{- d x}{\sqrt{1 - x^{2}}} = \frac{- d x}{\sqrt{1 - {c o s}^{2} t}}$ $d x = - s i n (t) d t$ $A = - \int_{π / 2}^{0} s i n (t) c o s (n t) d t$ $= \int_{0}^{π / 2} s i n (t) c o s (n t) d t$ $b y p a r t s$ $u = c o s (n t) \Rightarrow u^{'} = - n s i n (n t)$ $v^{'} = s i n (t) \Rightarrow v = - c o s (t)$ $A = - {[c o s (t) c o s (n t)]}_{0}^{π / 2} - n \int_{0}^{π / 2} s i n (n t) c o s (t) d t$ $b y p a r t s$ $u = s i n (n t) \Rightarrow u^{'} = n c o s (n t)$ $v^{'} = c o s (t) \Rightarrow v = s i n (t)$ $A = 1 - n {[s i n (t) s i n (n t)]}_{0}^{π / 2} + n^{2} \int_{0}^{π / 2} s i n (t) c o s (n t) d t$ $A = 1 - n s i n (\frac{n π}{2}) + n^{2} A$ $A (1 - n^{2}) = 1 - n s i n (\frac{n π}{2})$ $A = \frac{n s i n (\frac{n π}{2}) - 1}{n^{2} - 1}$
	Commented by Abdo msup. last updated on 13/Dec/18

	$t h a n k s s i r S m a i l . .$
	Commented by Smail last updated on 14/Dec/18

	$y o u a r e q u i t e w e l c o m e$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum