Question and Answers Forum
Question Number 49964 by ajfour last updated on 12/Dec/18
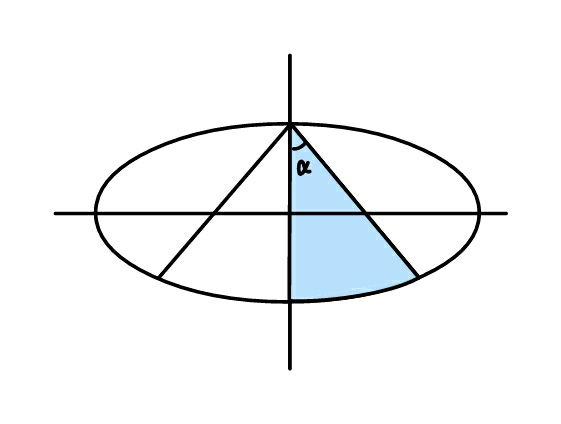
Commented by ajfour last updated on 12/Dec/18
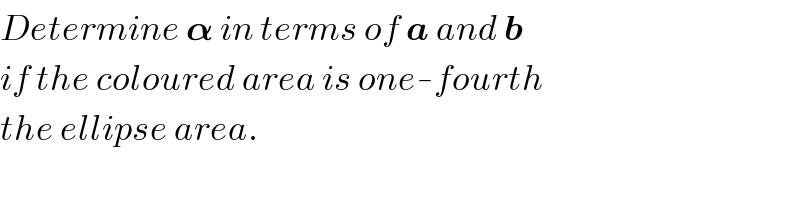
Commented by MJS last updated on 13/Dec/18
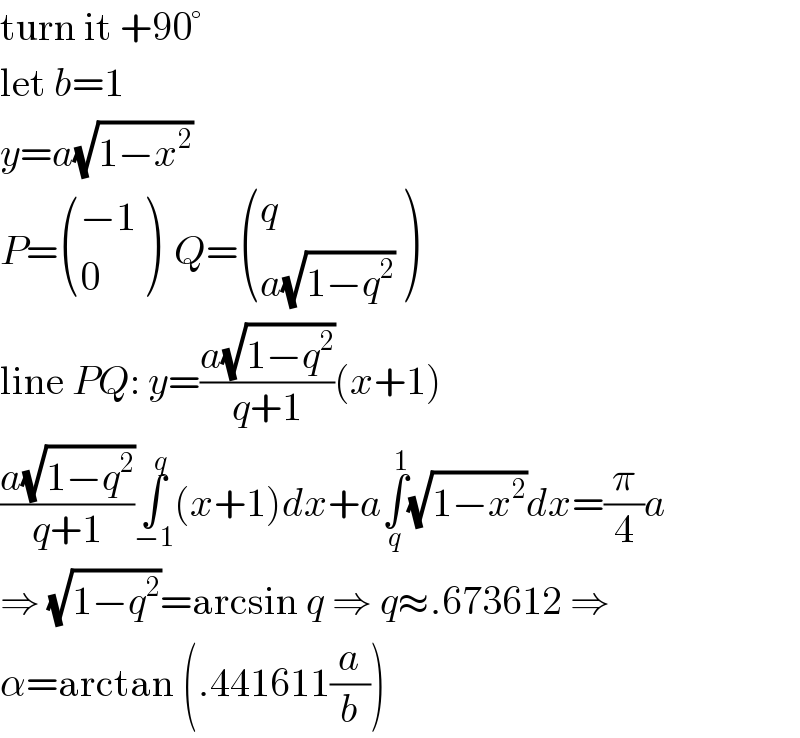
Answered by mr W last updated on 13/Dec/18
![y−b=−(x/(tan α))=−kx r sin θ−b=−kr cos θ r=(b/(sin θ+k cos θ)) r^2 (((cos^2 θ)/a^2 )+((sin^2 θ)/b^2 ))=1 r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ))=(b^2 /(sin^2 θ+λ^2 cos^2 θ)) with λ=(b/a) (b^2 /((sin θ+k cos θ)^2 ))=(b^2 /(sin^2 θ+λ^2 cos^2 θ)) (1/((tan θ+k)^2 ))=(1/(tan^2 θ+λ^2 )) ⇒tan^2 θ+2k tan θ+k^2 =tan^2 θ+λ^2 ⇒tan θ_1 =((λ^2 −k^2 )/(2k)) ⇒θ_1 =tan^(−1) ((λ^2 −k^2 )/(2k)) ∫_θ_1 ^(π/2) (1/2)[(b^2 /(sin^2 θ+λ^2 cos^2 θ))−(b^2 /((sin θ+k cos θ)^2 ))]dθ=((πab)/4) ∫_θ_1 ^(π/2) [(1/(sin^2 θ+λ^2 cos^2 θ))−(1/((sin θ+k cos θ)^2 ))]dθ=(π/(2λ)) [(1/λ) tan^(−1) ((tan θ)/λ)+(1/(k+tan θ))]_θ_1 ^(π/2) =(π/(2λ)) [(1/λ)((π/2)−tan^(−1) ((λ^2 −k^2 )/(2λk)))−(1/(k+((λ^2 −k^2 )/(2k))))]=(π/(2λ)) [(1/λ)((π/2)−tan^(−1) ((λ^2 −k^2 )/(2λk)))−((2k)/(λ^2 +k^2 ))]=(π/(2λ)) tan^(−1) ((k^2 −λ^2 )/(2λk))=((2λk)/(k^2 +λ^2 )) tan^(−1) ((2λk)/(k^2 −λ^2 ))+((2λk)/(k^2 +λ^2 ))=(π/2) with μ=(k/λ) tan^(−1) (2/(μ−(1/μ)))+(2/(μ+(1/μ)))=(π/2) ⇒μ=(k/λ)=2.2644 ⇒k=(1/(tan α))=2.2644λ=2.2644(b/a) ⇒α=tan^(−1) ((0.4416a)/b)](Q50031.png)
Commented by mr W last updated on 13/Dec/18
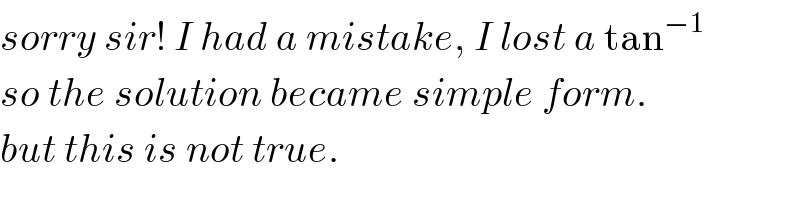
Commented by MJS last updated on 13/Dec/18
Commented by MJS last updated on 13/Dec/18

Commented by mr W last updated on 13/Dec/18
Commented by ajfour last updated on 13/Dec/18