
Question and Answers Forum
Question Number 85153 by reprins last updated on 19/Mar/20
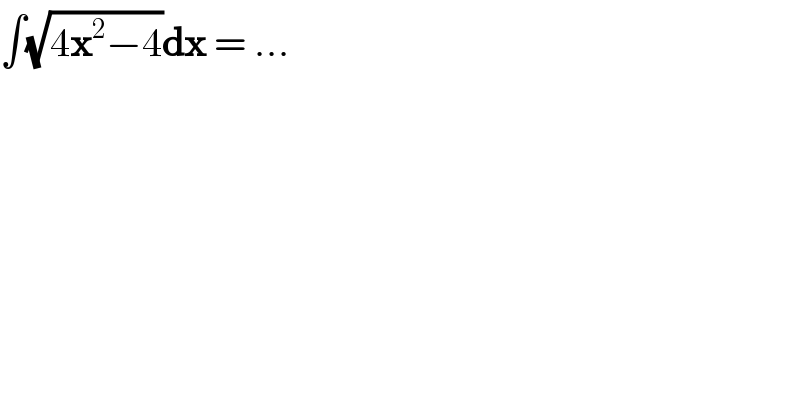
Commented by mathmax by abdo last updated on 19/Mar/20

Answered by john santu last updated on 19/Mar/20
![2∫(√(x^2 −1)) dx =K let x = sec t K= 2∫ (√(sec^2 t−1)) sec t tan t dt K= 2 ∫ sec t tan^2 t dt K = 2[∫ sec^3 t dt − ln ∣sec t + tan t ∣ ] for I= ∫ sec^3 t dt = ∫ sec t d(tan t) I = sec t tan t − ∫ tan^2 t sec t dt I = sec t tan t − ∫ sec^3 t dt + ln ∣sec t+tan t∣ 2I = sec t tan t + ln ∣sec t+tan t∣ I = (1/2)sec t tan t +(1/2) ln ∣sec t+tan t∣ K = sec t tan t − ln ∣sec t+tan t∣ + c ∴ K = x(√(x^2 −1 )) −ln ∣x+(√(x^2 −1)) ∣ +c](Q85221.png)
| ||
Question and Answers Forum | ||
Question Number 85153 by reprins last updated on 19/Mar/20 | ||
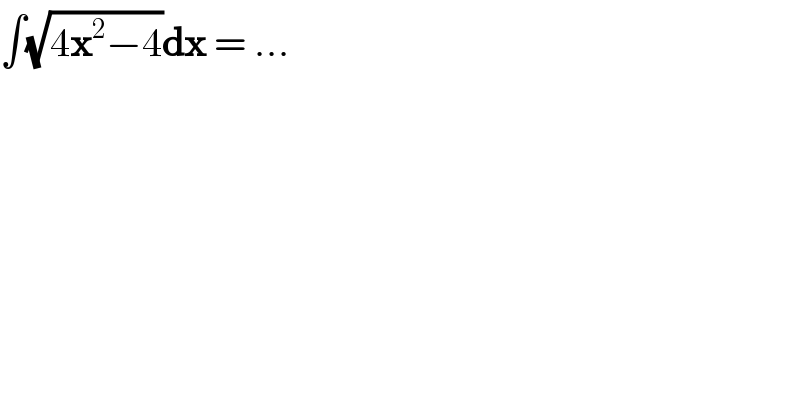 | ||
Commented by mathmax by abdo last updated on 19/Mar/20 | ||
 | ||
Answered by john santu last updated on 19/Mar/20 | ||
![2∫(√(x^2 −1)) dx =K let x = sec t K= 2∫ (√(sec^2 t−1)) sec t tan t dt K= 2 ∫ sec t tan^2 t dt K = 2[∫ sec^3 t dt − ln ∣sec t + tan t ∣ ] for I= ∫ sec^3 t dt = ∫ sec t d(tan t) I = sec t tan t − ∫ tan^2 t sec t dt I = sec t tan t − ∫ sec^3 t dt + ln ∣sec t+tan t∣ 2I = sec t tan t + ln ∣sec t+tan t∣ I = (1/2)sec t tan t +(1/2) ln ∣sec t+tan t∣ K = sec t tan t − ln ∣sec t+tan t∣ + c ∴ K = x(√(x^2 −1 )) −ln ∣x+(√(x^2 −1)) ∣ +c](Q85221.png) | ||
| ||