Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 92888 by s.ayeni14@yahoo.com last updated on 09/May/20

$$\int \frac{5-\mathrm{t}}{1+\sqrt{(\mathrm{t}-4)}}\mathrm{dt}$$$$$$

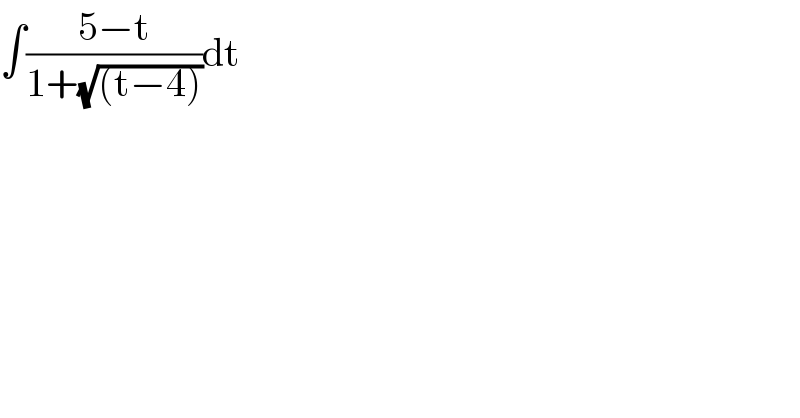
Commented by mathmax by abdo last updated on 09/May/20

$$I=\int \frac{5-t}{1+\sqrt{t-4}}dtwedothechangement\sqrt{t-4}=x\Rightarrow t-4=x^2\Rightarrow$$$$I=\int \frac{5-(x^2+4)}{1+x}\left(2x\right)dx=2\int \frac{1-x^2}{1+x}xdx$$$$=2\int (1-x)xdx=2\int (x-x^2)dx=2(\frac{x^2}{2}-\frac{1}{3}{x}^3)+C$$$$=x^2-\frac{2}{3}{x}^3+C=t-4-\frac{2}{3}(t-4)\sqrt{t-4}+C$$

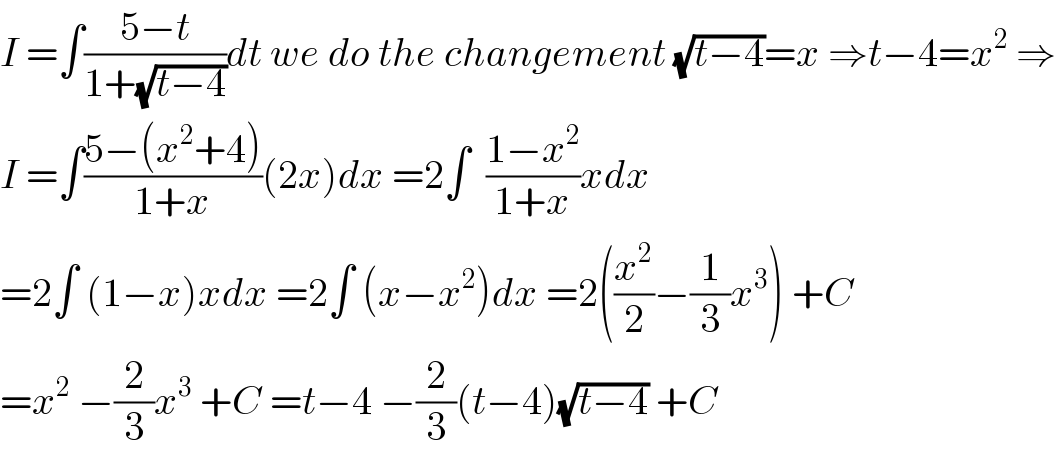
Commented by john santu last updated on 09/May/20

$$\sqrt{\mathrm{t}-4}=\mathrm{u}\Rightarrow \mathrm{dt}=2\mathrm{u}\mathrm{du}$$$$\int \frac{5-({\mathrm{u}}^2+4)2\mathrm{u}\mathrm{du}}{1+\mathrm{u}}=$$$$\int \frac{(1-\mathrm{u})(1+\mathrm{u})2\mathrm{u}\mathrm{du}}{1+\mathrm{u}}=$$$$\int (2\mathrm{u}-{2\mathrm{u}}^2)\mathrm{du}={\mathrm{u}}^2-\frac{2}{3}{\mathrm{u}}^3+\mathrm{c}$$$$=\frac{2}{3}{\mathrm{u}}^2(\frac{3}{2}-\mathrm{u})+\mathrm{c}$$$$=\frac{2}{3}(\mathrm{t}-4)(\frac{3}{2}-\sqrt{\mathrm{t}-4})+\mathrm{c}$$

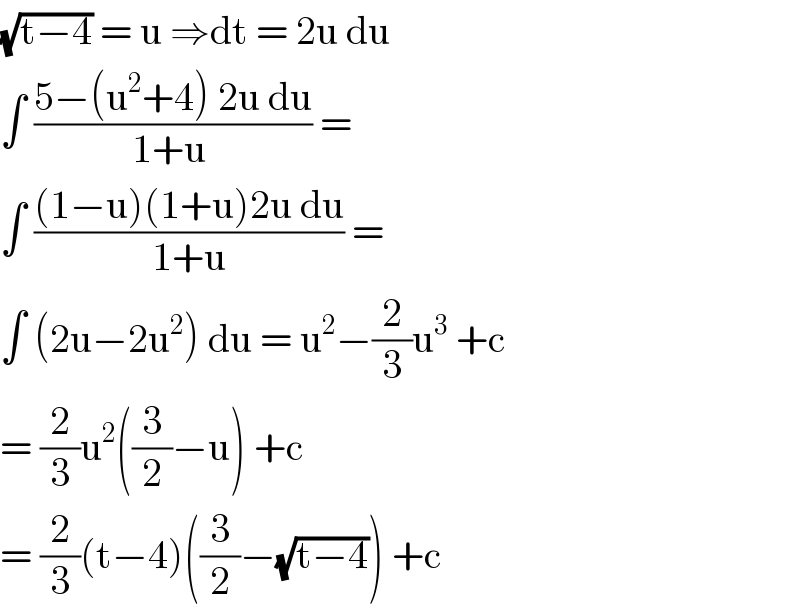
Commented by s.ayeni14@yahoo.com last updated on 09/May/20

$$\mathrm{thank}\mathrm{you}$$

Answered by maths mind last updated on 10/May/20

$$5-t=1-(t-4)$$$$=(1-\sqrt{t-4})(1+\sqrt{t-4})$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com