if y^x =x^y and y and x are both not equal to 0 and l find the value of x and y


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 50064 by mondodotto@gmail.com last updated on 13/Dec/18

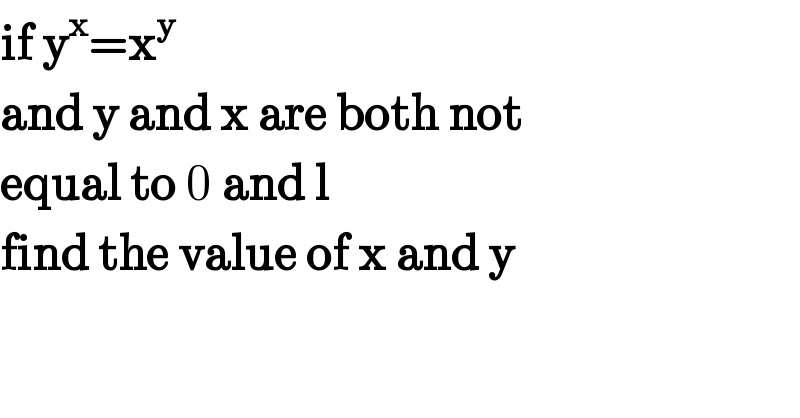
$if y^{x} = x^{y}$ $and y and x are both not$ $equal to 0 and l$ $find the value of x and y$
	Answered by Necxx last updated on 13/Dec/18

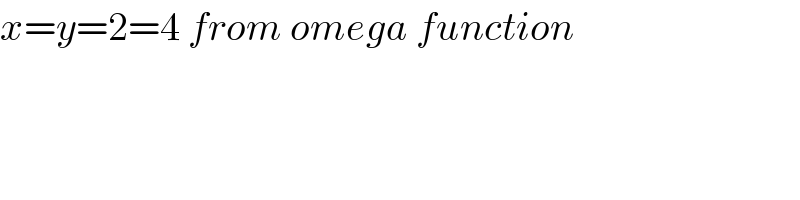
	$x = y = 2 = 4 f r o m o m e g a f u n c t i o n$
	Answered by mr W last updated on 14/Dec/18
	$there are infinite solutions. x=y=a is a solution with a∈R ∪ a>0 x=a y^a =a^y y=a^(y/a) y=e^((ln a)(y/a)) ye^(−(ln a)(y/a)) =1 −(ln a)(y/a)e^(−(ln a)(y/a)) =−((ln a)/a) −(ln a)(y/a)=W(−((ln a)/a)) (Lambert W function) ⇒y=−(a/(ln a))W(−((ln a)/a)) ⇒solution is { ((x=a, a∈R and a>0)),((y=a)) :} { ((x=a, a∈R and a>1)),((y=−(a/(ln a))W(−((ln a)/a)))) :} examples: x=(1/2): y=(1/(2ln 2))W(2ln 2)=((0.6931)/(2ln 2))=0.5 x=2: y=−(2/(ln 2))W(−((ln 2)/2))= { ((−(2/(ln 2))×(−0.6931)=2)),((−(2/(ln 2))×(−1.3863)=4)) :} x=5: y=−(5/(ln 5))W(−((ln 5)/5))= { ((−(5/(ln 5))×(−0.5681)=1.7649)),((−(5/(ln 5))×(−1.6094)=5)) :}$
	$t h e r e a r e i n f i n i t e s o l u t i o n s .$ $x = y = a i s a s o l u t i o n w i t h a \in R \cup a > 0$ $x = a$ $y^{a} = a^{y}$ $y = a^{\frac{y}{a}}$ $y = e^{(\ln a) \frac{y}{a}}$ ${y e}^{- (\ln a) \frac{y}{a}} = 1$ $- (\ln a) \frac{y}{a} e^{- (\ln a) \frac{y}{a}} = - \frac{\ln a}{a}$ $- (\ln a) \frac{y}{a} = W (- \frac{\ln a}{a}) (L a m b e r t W f u n c t i o n)$ $\Rightarrow y = - \frac{a}{\ln a} W (- \frac{\ln a}{a})$ $\Rightarrow s o l u t i o n i s$ ${\begin{cases} x = a, a \in R a n d a > 0 \\ y = a \end{cases}$ ${\begin{cases} x = a, a \in R a n d a > 1 \\ y = - \frac{a}{\ln a} W (- \frac{\ln a}{a}) \end{cases}$ $e x a m p l e s :$ $x = \frac{1}{2} :$ $y = \frac{1}{2 \ln 2} W (2 \ln 2) = \frac{0.6931}{2 \ln 2} = 0.5$ $x = 2 :$ $y = - \frac{2}{\ln 2} W (- \frac{\ln 2}{2}) = {\begin{cases} - \frac{2}{\ln 2} \times (- 0.6931) = 2 \\ - \frac{2}{\ln 2} \times (- 1.3863) = 4 \end{cases}$ $x = 5 :$ $y = - \frac{5}{\ln 5} W (- \frac{\ln 5}{5}) = {\begin{cases} - \frac{5}{\ln 5} \times (- 0.5681) = 1.7649 \\ - \frac{5}{\ln 5} \times (- 1.6094) = 5 \end{cases}$
	Commented by Pk1167156@gmail.com last updated on 14/Dec/18
	you are right sir.
	Commented by Pk1167156@gmail.com last updated on 14/Dec/18
	but only for x=y
	Commented by mr W last updated on 14/Dec/18
	$why did you say only for x=y? as I have proved: for 0<x≤1 there is only one value for y, and it is y=x. but for x>1, there are always^(∗)) two values for y, they are y=−(x/(ln x))W(−((ln x)/x)), this W−function delivers two results, i.e. one value of y is x, the other one is not x. for example if x=2, y=−(2/(ln 2))W(−((ln 2)/2))= { (2),(4) :} so we have two solutions: (2,2) and (2,4). you can check: 2^2 =2^2 and 2^4 =4^2 . ^(∗)) exception: when ((ln x)/x)=(1/e) or x=e, y=−(x/(ln x))W(−((ln x)/x)) has only one value: y=e=x.$
	$w h y d i d y o u s a y o n l y f o r x = y ?$ $a s I h a v e p r o v e d :$ $f o r 0 < x ⩽ 1 t h e r e i s o n l y o n e v a l u e f o r y,$ $a n d i t i s y = x .$ $b u t f o r x > 1, t h e r e a r e {a l w a y s}^{)} t w o v a l u e s$ $f o r y, t h e y a r e y = - \frac{x}{\ln x} W (- \frac{\ln x}{x}), t h i s$ $W - f u n c t i o n d e l i v e r s t w o r e s u l t s, i . e .$ $o n e v a l u e o f y i s x, t h e o t h e r o n e i s n o t x .$ $f o r e x a m p l e i f x = 2, y = - \frac{2}{\ln 2} W (- \frac{\ln 2}{2}) = {\begin{cases} 2 \\ 4 \end{cases}$ $s o w e h a v e t w o s o l u t i o n s : (2, 2) a n d$ $(2, 4) . y o u c a n c h e c k :$ $2^{2} = 2^{2} a n d 2^{4} = 4^{2} .$ $^{)} e x c e p t i o n : w h e n \frac{\ln x}{x} = \frac{1}{e} o r x = e,$ $y = - \frac{x}{\ln x} W (- \frac{\ln x}{x}) h a s o n l y o n e v a l u e :$ $y = e = x .$
	Commented by mondodotto@gmail.com last updated on 14/Dec/18

	$thank you$
	Answered by mr W last updated on 15/Dec/18
	$an other way without using Lambert function the solution x=y=any real number >0 is clear. we only need to find the solution for x≠y. let y=λx (λx)^x =x^((λx)) λx=x^λ λ=x^(λ−1) ⇒x=λ^(1/(λ−1)) y=λ×λ^(1/(λ−1)) =λ^(1+(1/(λ−1))) ⇒y=λ^(λ/(λ−1)) i.e. the general solution is { ((x=λ^(1/(λ−1)) )),((y=λ^(λ/(λ−1)) )) :} with λ>1 examples: λ=2⇒x=2, y=4 λ=3⇒x=(√3), y=3(√3) λ=4⇒x=^3 (√4), y=4^3 (√4) ......$
	$a n o t h e r w a y w i t h o u t u s i n g L a m b e r t$ $f u n c t i o n$ $t h e s o l u t i o n x = y = a n y r e a l n u m b e r > 0$ $i s c l e a r . w e o n l y n e e d t o f i n d t h e$ $s o l u t i o n f o r x \neq y .$ $l e t y = λ x$ ${(λ x)}^{x} = x^{(λ x)}$ $λ x = x^{λ}$ $λ = x^{λ - 1}$ $\Rightarrow x = λ^{\frac{1}{λ - 1}}$ $y = λ \times λ^{\frac{1}{λ - 1}} = λ^{1 + \frac{1}{λ - 1}}$ $\Rightarrow y = λ^{\frac{λ}{λ - 1}}$ $i . e . t h e g e n e r a l s o l u t i o n i s$ ${\begin{cases} x = λ^{\frac{1}{λ - 1}} \\ y = λ^{\frac{λ}{λ - 1}} \end{cases} w i t h λ > 1$ $e x a m p l e s :$ $λ = 2 \Rightarrow x = 2, y = 4$ $λ = 3 \Rightarrow x = \sqrt{3}, y = 3 \sqrt{3}$ $λ = 4 \Rightarrow x =^{3} \sqrt{4}, y = 4^{3} \sqrt{4}$ $. . . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum