
Question Number 50065 by peter frank last updated on 13/Dec/18

Answered by math1967 last updated on 13/Dec/18
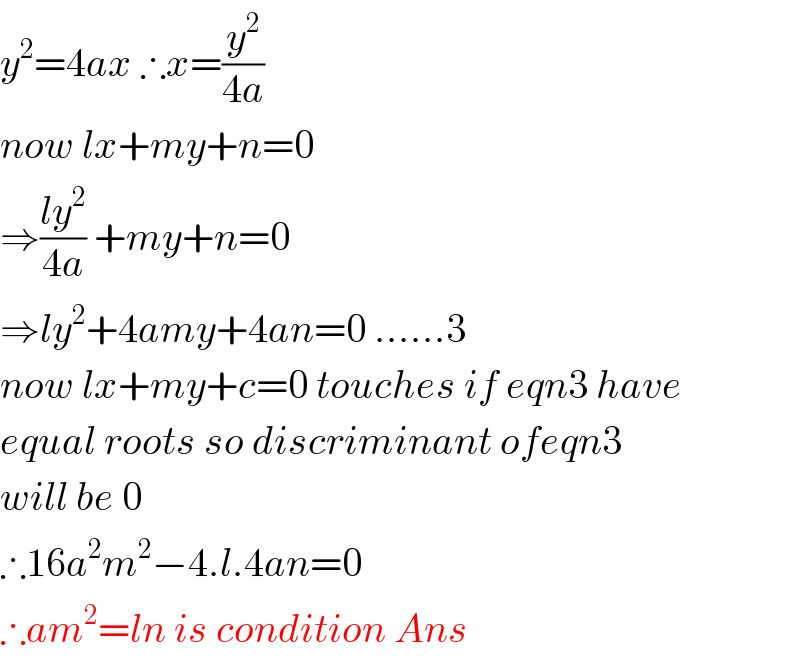
$${y}^{\mathrm{2}} =\mathrm{4}{ax}\:\therefore{x}=\frac{{y}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$${now}\:{lx}+{my}+{n}=\mathrm{0} \\ $$$$\Rightarrow\frac{{ly}^{\mathrm{2}} }{\mathrm{4}{a}}\:+{my}+{n}=\mathrm{0} \\ $$$$\Rightarrow{ly}^{\mathrm{2}} +\mathrm{4}{amy}+\mathrm{4}{an}=\mathrm{0}\:......\mathrm{3} \\ $$$${now}\:{lx}+{my}+{c}=\mathrm{0}\:{touches}\:{if}\:{eqn}\mathrm{3}\:{have} \\ $$$${equal}\:{roots}\:{so}\:{discriminant}\:{ofeqn}\mathrm{3} \\ $$$${will}\:{be}\:\mathrm{0} \\ $$$$\therefore\mathrm{16}{a}^{\mathrm{2}} {m}^{\mathrm{2}} −\mathrm{4}.{l}.\mathrm{4}{an}=\mathrm{0} \\ $$$$\therefore{am}^{\mathrm{2}} ={ln}\:{is}\:{condition}\:{Ans} \\ $$
Commented by peter frank last updated on 13/Dec/18

$${thank}\:{you}\: \\ $$
Commented by math1967 last updated on 14/Dec/18

$${welcome} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Dec/18
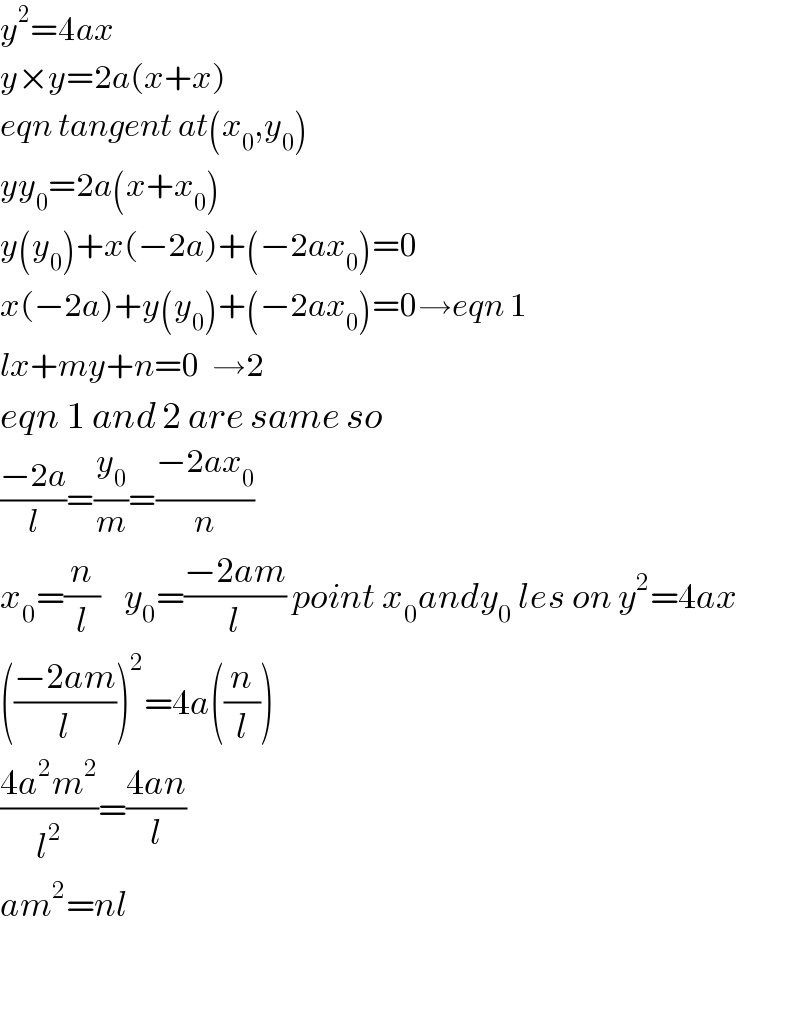
$${y}^{\mathrm{2}} =\mathrm{4}{ax} \\ $$$${y}×{y}=\mathrm{2}{a}\left({x}+{x}\right) \\ $$$${eqn}\:{tangent}\:{at}\left({x}_{\mathrm{0}} ,{y}_{\mathrm{0}} \right) \\ $$$${yy}_{\mathrm{0}} =\mathrm{2}{a}\left({x}+{x}_{\mathrm{0}} \right) \\ $$$${y}\left({y}_{\mathrm{0}} \right)+{x}\left(−\mathrm{2}{a}\right)+\left(−\mathrm{2}{ax}_{\mathrm{0}} \right)=\mathrm{0} \\ $$$${x}\left(−\mathrm{2}{a}\right)+{y}\left({y}_{\mathrm{0}} \right)+\left(−\mathrm{2}{ax}_{\mathrm{0}} \right)=\mathrm{0}\rightarrow{eqn}\:\mathrm{1} \\ $$$${lx}+{my}+{n}=\mathrm{0}\:\:\rightarrow\mathrm{2} \\ $$$${eqn}\:\mathrm{1}\:{and}\:\mathrm{2}\:{are}\:{same}\:{so} \\ $$$$\frac{−\mathrm{2}{a}}{{l}}=\frac{{y}_{\mathrm{0}} }{{m}}=\frac{−\mathrm{2}{ax}_{\mathrm{0}} }{{n}} \\ $$$${x}_{\mathrm{0}} =\frac{{n}}{{l}}\:\:\:\:{y}_{\mathrm{0}} =\frac{−\mathrm{2}{am}}{{l}}\:{point}\:{x}_{\mathrm{0}} {andy}_{\mathrm{0}} \:{les}\:{on}\:{y}^{\mathrm{2}} =\mathrm{4}{ax} \\ $$$$\left(\frac{−\mathrm{2}{am}}{{l}}\right)^{\mathrm{2}} =\mathrm{4}{a}\left(\frac{{n}}{{l}}\right) \\ $$$$\frac{\mathrm{4}{a}^{\mathrm{2}} {m}^{\mathrm{2}} }{{l}^{\mathrm{2}} }=\frac{\mathrm{4}{an}}{{l}} \\ $$$${am}^{\mathrm{2}} ={nl} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 13/Dec/18

$${thank}\:{you} \\ $$
Answered by peter frank last updated on 13/Dec/18
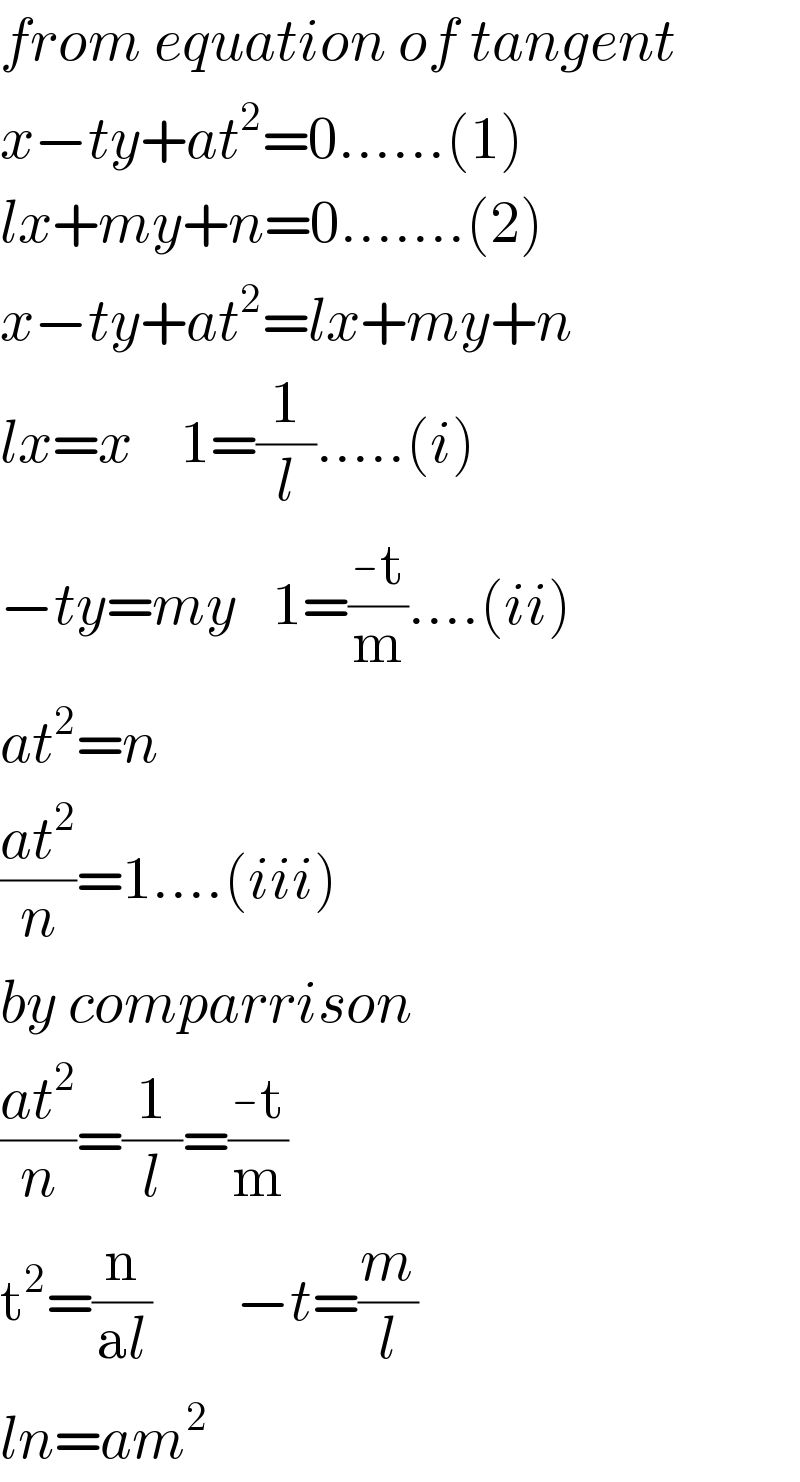
$${from}\:{equation}\:{of}\:{tangent} \\ $$$${x}−{ty}+{at}^{\mathrm{2}} =\mathrm{0}......\left(\mathrm{1}\right) \\ $$$${lx}+{my}+{n}=\mathrm{0}.......\left(\mathrm{2}\right) \\ $$$${x}−{ty}+{at}^{\mathrm{2}} ={lx}+{my}+{n} \\ $$$${lx}={x}\:\:\:\:\mathrm{1}=\frac{\mathrm{1}}{{l}}.....\left({i}\right) \\ $$$$−{ty}={my}\:\:\:\mathrm{1}=\frac{-\mathrm{t}}{\mathrm{m}}....\left({ii}\right) \\ $$$${at}^{\mathrm{2}} ={n} \\ $$$$\frac{{at}^{\mathrm{2}} }{{n}}=\mathrm{1}....\left({iii}\right) \\ $$$${by}\:{comparrison} \\ $$$$\frac{{at}^{\mathrm{2}} }{{n}}=\frac{\mathrm{1}}{{l}}=\frac{-\mathrm{t}}{\mathrm{m}} \\ $$$$\mathrm{t}^{\mathrm{2}} =\frac{\mathrm{n}}{\mathrm{a}{l}}\:\:\:\:\:\:\:−{t}=\frac{{m}}{{l}} \\ $$$${ln}={am}^{\mathrm{2}} \\ $$
