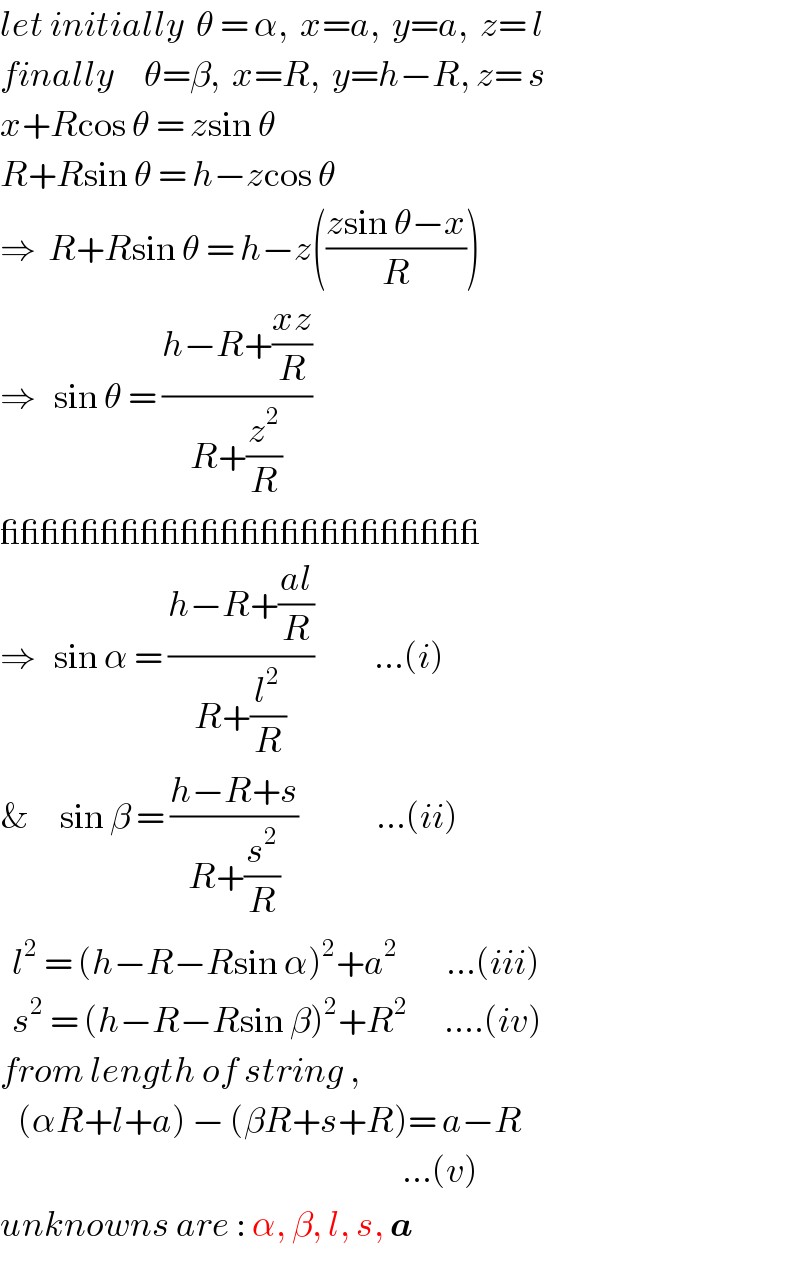Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 50101 by ajfour last updated on 13/Dec/18

Commented by ajfour last updated on 14/Dec/18

$I f s y s t e m o f r i n g a n d b l o c k b e$ $r e l e a s e d a s s h o w n, a n d l a t e r t h e$ $r i n g h i t s t h e b l o c k a s s h o w n i n$ $d a s h e d l i n e s, d e t e r m i n e a .$ $F i n d a l s o t h e v e l o c i t y o f r i n g t h e n .$ $A s s u m e f r i c t i o n s u f f i c i e n t s u c h$ $t h a t r i n g r o l l s p u r e l y a s i t m o v e s .$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

$p l s m e n t i o n t h e s o u r c e o f q u e s t i o n a n d a l s o$ $a t t a c h t h e f i n a l a n s w e r . . . s o t h a t w e c a n$ $f o l l o w t h e r i g h t p a t h t o g e t t h e a n s w e r . . .$ $b e c a u s e q u e s t i o n i t s e l f i s n o t c l e a r . . .$ $1) i f t h e t h r e a d g e t s u n w i n d e d . . . t h e r i n g h a s$ $a t e n d e n c y t o r o t a t e a n t i c l o c k w i s e . . .$ $f u r t h e r w e i g h t o f b l o c k M g c a u s e t h e r i n g$ $t o g e t u n w i n d e d . . .$
Commented by ajfour last updated on 14/Dec/18

$w h i c h w a y d o y o u t h i n k n e t t o r q u e$ $o n r i n g s h a l l b e, T a n m a y S i r;$ $i s e l d o m p o s t q u e s t i o n s f r o m$ $s o u r c e s .$
Commented by mr W last updated on 14/Dec/18

$t o m e t h e q u e s t i o n i s c l e a r a n d u n i q u e . t h e$ $t h r e a d k e e p s i n t e n s i o n .$
	Answered by mr W last updated on 14/Dec/18
	$let θ=angle between string and ground length of string at t=0: a+(R/(tan (θ_0 /2)))=(h/(tan θ_0 ))=((h(1−tan^2 (θ_0 /2)))/(2tan (θ_0 /2))) δ_0 =tan (θ_0 /2) a+(R/δ_0 )=((h(1−δ_0 ^2 ))/(2δ_0 )) a=((h(1−δ_0 ^2 )−2R)/(2δ_0 )) δ_0 ^2 +2((a/h))δ_0 −(1−((2R)/h))=0 with α=(a/h) and γ=(R/h) δ_0 ^2 +2αδ_0 −(1−2γ)=0 ⇒δ_0 =(√(1+α^2 −2γ))−α=tan (θ_0 /2) l_0 =a+(h/(sin θ_0 ))−(R/(tan (θ_0 /2))) l_0 =a+((h−2R+hδ_0 ^2 )/(2δ_0 )) length of string at t=t_1 : R+(R/(tan (θ_1 /2)))=(h/(tan θ_1 ))=((h(1−tan^2 (θ_1 /2)))/(2tan (θ_1 /2))) R+(R/δ_1 )=((h(1−δ_1 ^2 ))/(2δ_1 )) R=((h(1−δ_1 ^2 )−2R)/(2δ_1 )) 2Rδ_1 =h−2R−hδ_1 ^2 δ_1 ^2 +2γδ_1 −(1−2γ)=0 ⇒δ_1 =(√(γ^2 +1−2γ))−γ=tan (θ_1 /2) l_1 =h−R+(h/(sin θ_1 ))−(R/(tan (θ_1 /2))) l_1 =h−R+((h−2R+hδ_1 ^2 )/(2δ_1 )) l_1 =l_0 +a−R h−R+((h−2R+hδ_1 ^2 )/(2δ_1 ))=a+((h−2R+hδ_0 ^2 )/(2δ_0 ))+a−R h+((h−2R+hδ_1 ^2 )/(2δ_1 ))=2a+((h−2R+hδ_0 ^2 )/(2δ_0 )) 1+((1−2γ+δ_1 ^2 )/(2δ_1 ))=2α+((1−2γ+δ_0 ^2 )/(2δ_0 )) ((1−2γ)/δ_1 )+δ_1 −((1−2γ)/δ_0 )−δ_0 =2(2α−1) ((1−2γ)/((√(γ^2 +1−2γ))−γ))+(√(γ^2 +1−2γ))−γ−((1−2γ)/((√(1+α^2 −2γ))−α))−(√(1+α^2 −2γ))+α=4α−2 ⇒3α+((1−2γ)/((√(1+α^2 −2γ))−α))+(√(1+α^2 −2γ))=2−γ+((1−2γ)/((√(γ^2 +1−2γ))−γ))+(√(γ^2 +1−2γ)) γ is constant, α is unknown ⇒solve for α=.... ⇒a=αh=..... at time t: position of block is y (above ground) position of ring is x x+(R/(tan (θ/2)))=(h/(tan θ))=((h(1−tan^2 (θ/2)))/(2tan (θ/2))) x+(R/δ)=((h(1−δ^2 ))/(2δ)) x=((h−2R−hδ^2 )/(2δ)) λ=(x/h)=((1−2γ−δ^2 )/(2δ)) δ^2 +2λδ−(1−2γ)=0 ⇒δ=(√(1+λ^2 −2γ))−λ (dδ/dt)=((λ/(√(1+λ^2 −2γ)))−1)(1/h)×(dx/dt) l=h−y+(h/(sin θ))−(R/(tan (θ/2))) l=h−y+((h−2R+hδ^2 )/(2δ))=l_0 +a−x 1−(y/h)+((1−2γ+δ^2 )/(2δ))=2α+((1−2γ+δ_0 ^2 )/(2δ_0 ))−λ v_y =−(dy/dt)=velocity of block v=−(dx/dt)=velocity of ring (v_y /h)+[1−((1−2γ+δ^2 )/(2δ^2 ))](dδ/dt)=(v/h) (v_y /h)−(((δ^2 −1+2γ)/(2δ^2 )))((λ/(√(1+λ^2 −2γ)))−1)(v/h)=(v/h) v_y ={1+(((δ^2 −1+2γ)/(2δ^2 )))((λ/(√(1+λ^2 −2γ)))−1)}v at t=t_1 : δ=δ_1 , x=R, λ=(R/h)=γ v_y ={1+((((√(γ^2 +1−2γ))−γ)^2 −1+2γ)/(2((√(γ^2 +1−2γ))−γ)^2 ))((γ/(√(1+γ^2 −2γ)))−1)}v ⇒v_y ={1+((γ(1−2γ))/((1−γ)((√(γ^2 +1−2γ))−γ)))}v (1/2)Mv^2 +(1/2)(MR^2 )ω^2 +(1/2)Mv_y ^2 =Mg(h−a−R) 2v^2 +v_y ^2 =2gh(1−α−γ) [2+{1+((γ(1−2γ))/((1−γ)((√(γ^2 +1−2γ))−γ)))}^2 ]v^2 =2gh(1−α−γ) ⇒v=(√((2gh(1−α−γ))/(2+{1+((γ(1−2γ))/((1−γ)((√(γ^2 +1−2γ))−γ)))}^2 )))$
	$l e t θ = a n g l e b e t w e e n s t r i n g a n d g r o u n d$ $l e n g t h o f s t r i n g a t t = 0 :$ $a + \frac{R}{\tan \frac{θ_{0}}{2}} = \frac{h}{\tan θ_{0}} = \frac{h (1 - \tan^{2} \frac{θ_{0}}{2})}{2 \tan \frac{θ_{0}}{2}}$ $δ_{0} = \tan \frac{θ_{0}}{2}$ $a + \frac{R}{δ_{0}} = \frac{h (1 - δ_{0}^{2})}{2 δ_{0}}$ $a = \frac{h (1 - δ_{0}^{2}) - 2 R}{2 δ_{0}}$ $δ_{0}^{2} + 2 (\frac{a}{h}) δ_{0} - (1 - \frac{2 R}{h}) = 0$ $w i t h α = \frac{a}{h} a n d γ = \frac{R}{h}$ $δ_{0}^{2} + 2 α δ_{0} - (1 - 2 γ) = 0$ $\Rightarrow δ_{0} = \sqrt{1 + α^{2} - 2 γ} - α = \tan \frac{θ_{0}}{2}$ $l_{0} = a + \frac{h}{\sin θ_{0}} - \frac{R}{\tan \frac{θ_{0}}{2}}$ $l_{0} = a + \frac{h - 2 R + h δ_{0}^{2}}{2 δ_{0}}$ $l e n g t h o f s t r i n g a t t = t_{1} :$ $R + \frac{R}{\tan \frac{θ_{1}}{2}} = \frac{h}{\tan θ_{1}} = \frac{h (1 - \tan^{2} \frac{θ_{1}}{2})}{2 \tan \frac{θ_{1}}{2}}$ $R + \frac{R}{δ_{1}} = \frac{h (1 - δ_{1}^{2})}{2 δ_{1}}$ $R = \frac{h (1 - δ_{1}^{2}) - 2 R}{2 δ_{1}}$ $2 R δ_{1} = h - 2 R - h δ_{1}^{2}$ $δ_{1}^{2} + 2 γ δ_{1} - (1 - 2 γ) = 0$ $\Rightarrow δ_{1} = \sqrt{γ^{2} + 1 - 2 γ} - γ = \tan \frac{θ_{1}}{2}$ $l_{1} = h - R + \frac{h}{\sin θ_{1}} - \frac{R}{\tan \frac{θ_{1}}{2}}$ $l_{1} = h - R + \frac{h - 2 R + h δ_{1}^{2}}{2 δ_{1}}$ $l_{1} = l_{0} + a - R$ $h - R + \frac{h - 2 R + h δ_{1}^{2}}{2 δ_{1}} = a + \frac{h - 2 R + h δ_{0}^{2}}{2 δ_{0}} + a - R$ $h + \frac{h - 2 R + h δ_{1}^{2}}{2 δ_{1}} = 2 a + \frac{h - 2 R + h δ_{0}^{2}}{2 δ_{0}}$ $1 + \frac{1 - 2 γ + δ_{1}^{2}}{2 δ_{1}} = 2 α + \frac{1 - 2 γ + δ_{0}^{2}}{2 δ_{0}}$ $\frac{1 - 2 γ}{δ_{1}} + δ_{1} - \frac{1 - 2 γ}{δ_{0}} - δ_{0} = 2 (2 α - 1)$ $\frac{1 - 2 γ}{\sqrt{γ^{2} + 1 - 2 γ} - γ} + \sqrt{γ^{2} + 1 - 2 γ} - γ - \frac{1 - 2 γ}{\sqrt{1 + α^{2} - 2 γ} - α} - \sqrt{1 + α^{2} - 2 γ} + α = 4 α - 2$ $\Rightarrow 3 α + \frac{1 - 2 γ}{\sqrt{1 + α^{2} - 2 γ} - α} + \sqrt{1 + α^{2} - 2 γ} = 2 - γ + \frac{1 - 2 γ}{\sqrt{γ^{2} + 1 - 2 γ} - γ} + \sqrt{γ^{2} + 1 - 2 γ}$ $γ i s c o n s t a n t, α i s u n k n o w n$ $\Rightarrow s o l v e f o r α = . . . .$ $\Rightarrow a = α h = . . . . .$ $a t t i m e t :$ $p o s i t i o n o f b l o c k i s y (a b o v e g r o u n d)$ $p o s i t i o n o f r i n g i s x$ $x + \frac{R}{\tan \frac{θ}{2}} = \frac{h}{\tan θ} = \frac{h (1 - \tan^{2} \frac{θ}{2})}{2 \tan \frac{θ}{2}}$ $x + \frac{R}{δ} = \frac{h (1 - δ^{2})}{2 δ}$ $x = \frac{h - 2 R - h δ^{2}}{2 δ}$ $λ = \frac{x}{h} = \frac{1 - 2 γ - δ^{2}}{2 δ}$ $δ^{2} + 2 λ δ - (1 - 2 γ) = 0$ $\Rightarrow δ = \sqrt{1 + λ^{2} - 2 γ} - λ$ $\frac{d δ}{d t} = (\frac{λ}{\sqrt{1 + λ^{2} - 2 γ}} - 1) \frac{1}{h} \times \frac{d x}{d t}$ $l = h - y + \frac{h}{\sin θ} - \frac{R}{\tan \frac{θ}{2}}$ $l = h - y + \frac{h - 2 R + h δ^{2}}{2 δ} = l_{0} + a - x$ $1 - \frac{y}{h} + \frac{1 - 2 γ + δ^{2}}{2 δ} = 2 α + \frac{1 - 2 γ + δ_{0}^{2}}{2 δ_{0}} - λ$ $v_{y} = - \frac{d y}{d t} = v e l o c i t y o f b l o c k$ $v = - \frac{d x}{d t} = v e l o c i t y o f r i n g$ $\frac{v_{y}}{h} + [1 - \frac{1 - 2 γ + δ^{2}}{2 δ^{2}}] \frac{d δ}{d t} = \frac{v}{h}$ $\frac{v_{y}}{h} - (\frac{δ^{2} - 1 + 2 γ}{2 δ^{2}}) (\frac{λ}{\sqrt{1 + λ^{2} - 2 γ}} - 1) \frac{v}{h} = \frac{v}{h}$ $v_{y} = {1 + (\frac{δ^{2} - 1 + 2 γ}{2 δ^{2}}) (\frac{λ}{\sqrt{1 + λ^{2} - 2 γ}} - 1)} v$ $a t t = t_{1} : δ = δ_{1}, x = R, λ = \frac{R}{h} = γ$ $v_{y} = {1 + \frac{{(\sqrt{γ^{2} + 1 - 2 γ} - γ)}^{2} - 1 + 2 γ}{2 {(\sqrt{γ^{2} + 1 - 2 γ} - γ)}^{2}} (\frac{γ}{\sqrt{1 + γ^{2} - 2 γ}} - 1)} v$ $\Rightarrow v_{y} = {1 + \frac{γ (1 - 2 γ)}{(1 - γ) (\sqrt{γ^{2} + 1 - 2 γ} - γ)}} v$ $\frac{1}{2} {M v}^{2} + \frac{1}{2} ({M R}^{2}) ω^{2} + \frac{1}{2} {M v}_{y}^{2} = M g (h - a - R)$ $2 v^{2} + v_{y}^{2} = 2 g h (1 - α - γ)$ $[2 + {1 + \frac{γ (1 - 2 γ)}{(1 - γ) (\sqrt{γ^{2} + 1 - 2 γ} - γ)}}^{2}] v^{2} = 2 g h (1 - α - γ)$ $\Rightarrow v = \sqrt{\frac{2 g h (1 - α - γ)}{2 + {1 + \frac{γ (1 - 2 γ)}{(1 - γ) (\sqrt{γ^{2} + 1 - 2 γ} - γ)}}^{2}}}$
	Commented by ajfour last updated on 14/Dec/18

	$P l e n t i f u l o f m i n d a n d e f f o r t S i r;$ $t h a n k s, l e t m e t i m e t o f o l l o w i t$ $e n t i r e l y . .$
	Commented by mr W last updated on 14/Dec/18

	Commented by mr W last updated on 14/Dec/18

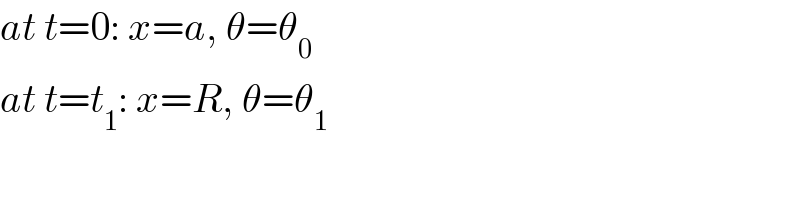
	$a t t = 0 : x = a, θ = θ_{0}$ $a t t = t_{1} : x = R, θ = θ_{1}$
	Commented by ajfour last updated on 16/Dec/18

	$V e r y b r i l l i a n t S i r, AWESOME!$
	Answered by ajfour last updated on 14/Dec/18

	Commented by ajfour last updated on 14/Dec/18

	$l e t i n i t i a l l y θ = α, x = a, y = a, z = l$ $f i n a l l y θ = β, x = R, y = h - R, z = s$ $x + R \cos θ = z \sin θ$ $R + R \sin θ = h - z \cos θ$ $\Rightarrow R + R \sin θ = h - z (\frac{z \sin θ - x}{R})$ $\Rightarrow \sin θ = \frac{h - R + \frac{x z}{R}}{R + \frac{z^{2}}{R}}$ $________________________$ $\Rightarrow \sin α = \frac{h - R + \frac{a l}{R}}{R + \frac{l^{2}}{R}} . . . (i)$ $& \sin β = \frac{h - R + s}{R + \frac{s^{2}}{R}} . . . (i i)$ $l^{2} = {(h - R - R \sin α)}^{2} + a^{2} . . . (i i i)$ $s^{2} = {(h - R - R \sin β)}^{2} + R^{2} . . . . (i v)$ $f r o m l e n g t h o f s t r i n g,$ $(α R + l + a) - (β R + s + R) = a - R$ $. . . (v)$ $u n k n o w n s a r e : α, β, l, s, a$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum