Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 50158 by cesar.marval.larez@gmail.com last updated on 14/Dec/18

Commented by cesar.marval.larez@gmail.com last updated on 14/Dec/18

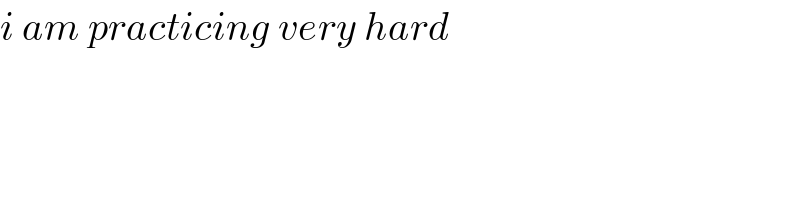
i am practicing very hard

$${i}\:{am}\:{practicing}\:{very}\:{hard} \\ $$

Answered by afachri last updated on 14/Dec/18

(4) ∫ ((2x^2 + 8x + 6)/(x − 3)) dx = .... let x − 3 = u ⇒ dx = du x = u + 3 then subtitute to eq ; ∫ ((2(u + 3)^2 + 8(u + 3) + 6 )/u) du = ∫ ((2u^2 + 20u + 48)/u) = ∫ 2u + 20 + ((48)/u) du = u^2 + 20u + 48 ln u + C = (x−3)^2 + 20(x−3) + 48 ln(x−3) + C = x^2 + 14x − 51 + 48 ln (x−3) + C

$$\left(\mathrm{4}\right)\:\:\:\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{8}{x}\:+\:\mathrm{6}}{{x}\:−\:\mathrm{3}}\:{dx}\:\:=\:\:\:.... \\ $$$$\boldsymbol{\mathrm{let}}\:\:\:{x}\:−\:\mathrm{3}\:\:=\:\:{u}\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:{dx}\:\:=\:\:{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\:=\:\:{u}\:+\:\mathrm{3}\:\:\boldsymbol{\mathrm{then}}\:\:\boldsymbol{\mathrm{subtitute}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{eq}}\:; \\ $$$$\int\:\:\frac{\mathrm{2}\left({u}\:+\:\mathrm{3}\right)^{\mathrm{2}} \:+\:\:\mathrm{8}\left({u}\:+\:\mathrm{3}\right)\:\:+\:\mathrm{6}\:}{{u}}\:\:{du}\:\:=\:\:\int\:\:\frac{\mathrm{2}{u}^{\mathrm{2}} \:+\:\mathrm{20}{u}\:+\:\mathrm{48}}{{u}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\int\:\:\mathrm{2}{u}\:+\:\mathrm{20}\:+\:\frac{\mathrm{48}}{{u}}\:\:\:\:{du}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:{u}^{\mathrm{2}} \:\:+\:\:\mathrm{20}{u}\:\:+\:\:\mathrm{48}\:\mathrm{ln}\:{u}\:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\left({x}−\mathrm{3}\right)^{\mathrm{2}} \:\:+\:\:\mathrm{20}\left({x}−\mathrm{3}\right)\:\:+\:\:\mathrm{48}\:\mathrm{ln}\left({x}−\mathrm{3}\right)\:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:{x}^{\mathrm{2}} +\:\:\mathrm{14}{x}\:−\:\mathrm{51}\:+\:\mathrm{48}\:\mathrm{ln}\:\left({x}−\mathrm{3}\right)\:+\:{C} \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

4)∫((2x^2 +3x+6)/(x−3))dx t=x−3 ∫((2(t+3)^2 +3(t+3)+6)/t)dt ∫((2t^2 +12t+18+3t+9+6)/t)dt ∫((2t^2 +15t+33)/t)dt 2∫tdt+15∫dt+33∫(dt/t) t^2 +15t+33lnt+c (x−3)^2 +15(x−3)+33ln(x−3)+c

$$\left.\mathrm{4}\right)\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{6}}{{x}−\mathrm{3}}{dx} \\ $$$${t}={x}−\mathrm{3}\: \\ $$$$\int\frac{\mathrm{2}\left({t}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{3}\left({t}+\mathrm{3}\right)+\mathrm{6}}{{t}}{dt} \\ $$$$\int\frac{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{12}{t}+\mathrm{18}+\mathrm{3}{t}+\mathrm{9}+\mathrm{6}}{{t}}{dt} \\ $$$$\int\frac{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{15}{t}+\mathrm{33}}{{t}}{dt} \\ $$$$\mathrm{2}\int{tdt}+\mathrm{15}\int{dt}+\mathrm{33}\int\frac{{dt}}{{t}} \\ $$$${t}^{\mathrm{2}} +\mathrm{15}{t}+\mathrm{33}{lnt}+{c} \\ $$$$\left({x}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{15}\left({x}−\mathrm{3}\right)+\mathrm{33}{ln}\left({x}−\mathrm{3}\right)+{c} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

5)∫cos^4 6x(−6sin6x)dx t=cos6x dt=−6sin6xdx ∫t^4 dt (t^5 /5)+c (((cos6x)^5 )/5)+c

$$\left.\mathrm{5}\right)\int{cos}^{\mathrm{4}} \mathrm{6}{x}\left(−\mathrm{6}{sin}\mathrm{6}{x}\right){dx} \\ $$$${t}={cos}\mathrm{6}{x}\:\:\:{dt}=−\mathrm{6}{sin}\mathrm{6}{xdx} \\ $$$$\int{t}^{\mathrm{4}} {dt} \\ $$$$\frac{{t}^{\mathrm{5}} }{\mathrm{5}}+{c}\:\:\:\: \\ $$$$\frac{\left({cos}\mathrm{6}{x}\right)^{\mathrm{5}} }{\mathrm{5}}+{c} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

6)∫sin^3 xdx ∫(1−cos^2 x)sinxdx t=cosx dt=−sinxdx ∫(1−t^2 )×−dt =(−1)(t−(t^3 /3))+c =(t^3 /3)−t+c =(((cosx)^3 )/3)−cosx+c

$$\left.\mathrm{6}\right)\int{sin}^{\mathrm{3}} {xdx} \\ $$$$\int\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){sinxdx} \\ $$$${t}={cosx}\:\:\:{dt}=−{sinxdx} \\ $$$$\int\left(\mathrm{1}−{t}^{\mathrm{2}} \right)×−{dt} \\ $$$$=\left(−\mathrm{1}\right)\left({t}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right)+{c} \\ $$$$=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−{t}+{c} \\ $$$$=\frac{\left({cosx}\right)^{\mathrm{3}} }{\mathrm{3}}−{cosx}+{c} \\ $$

Commented by cesar.marval.larez@gmail.com last updated on 14/Dec/18

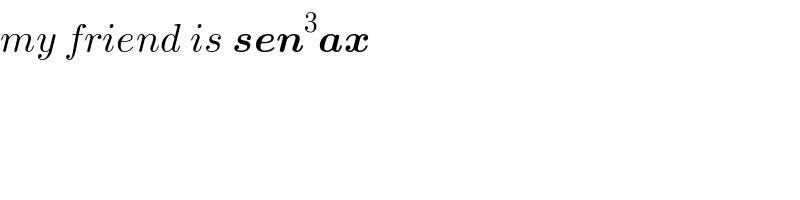
my friend is sen^3 ax

$${my}\:{friend}\:{is}\:\boldsymbol{{sen}}^{\mathrm{3}} \boldsymbol{{ax}} \\ $$

Commented by afachri last updated on 14/Dec/18

you can solve it over and do like Mr Chaudri did. and the result is : (((cos^3 (ax) − 3cos (ax))/(3a))) + C not too far isn′t it ?? don′t be doubt to try my friend.

$$\mathrm{you}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{over}\:\mathrm{and}\:\mathrm{do}\:\mathrm{like} \\ $$$$\mathrm{Mr}\:\mathrm{Chaudri}\:\mathrm{did}.\:\mathrm{and}\:\mathrm{the}\:\mathrm{result}\: \\ $$$$\mathrm{is}\:: \\ $$$$\:\:\left(\frac{\mathrm{cos}\:^{\mathrm{3}} \left({ax}\right)\:−\:\mathrm{3cos}\:\left({ax}\right)}{\mathrm{3}{a}}\right)\:+\:{C}\:\:\:\mathrm{not}\:\mathrm{too}\:\mathrm{far} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{isn}'\mathrm{t}\:\mathrm{it}\:?? \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{be}\:\mathrm{doubt}\:\mathrm{to}\:\mathrm{try}\:\mathrm{my}\:\mathrm{friend}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

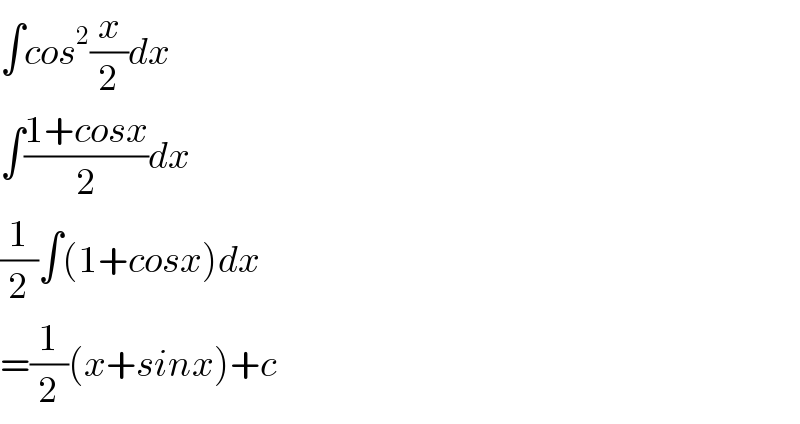
∫cos^2 (x/2)dx ∫((1+cosx)/2)dx (1/2)∫(1+cosx)dx =(1/2)(x+sinx)+c

$$\int{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$$\int\frac{\mathrm{1}+{cosx}}{\mathrm{2}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}+{cosx}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{sinx}\right)+{c} \\ $$

Commented by cesar.marval.larez@gmail.com last updated on 14/Dec/18

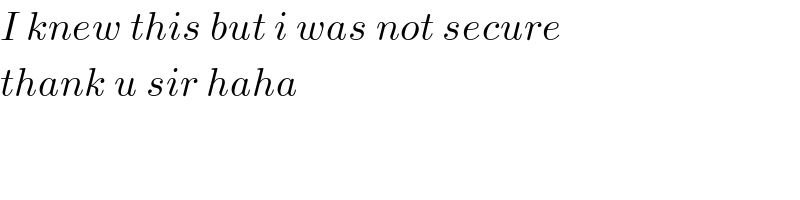
I knew this but i was not secure thank u sir haha

$${I}\:{knew}\:{this}\:{but}\:{i}\:{was}\:{not}\:{secure} \\ $$$${thank}\:{u}\:{sir}\:{haha} \\ $$

Answered by afachri last updated on 15/Dec/18

(9) ∫ 5x . e^((4x)/5) dx = ... Can be solved with partial integral ; ∫ u dv = uv − ∫ v du let u = 5x ⇒ du = 5 dx dv = e^((4x)/5) dx ⇒ v = (5/4) e^((4x)/5) so uv − ∫ v du = (5x . (5/4) e^((4x)/5) ) − ∫ (5/4) e^((4x)/5) (5 dx) = ((25x)/4) e^((4x)/5) − (((5×5)/(4×4)) e^((4x)/5) . 5) + C = ((25 e^((4x)/5) )/4) ( x − (5/4)) + C

$$\left(\mathrm{9}\right)\:\:\int\:\:\mathrm{5}{x}\:.\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} {dx}\:\:=\:\:\:... \\ $$$$\mathrm{Can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{with}\:\mathrm{partial}\:\mathrm{integral}\:\:; \\ $$$$\int\:\:{u}\:\:{dv}\:\:\:=\:\:\:{uv}\:\:−\:\int\:{v}\:\:{du} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{let}}\:\:\:\:\:\boldsymbol{{u}}\:\:=\:\:\mathrm{5}{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:{du}\:\:=\:\:\mathrm{5}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:{dv}\:\:=\:\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} \:{dx}\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:{v}\:\:\:\:=\:\:\frac{\mathrm{5}}{\mathrm{4}}\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} \: \\ $$$$\boldsymbol{\mathrm{so}}\:\:\:\:{uv}\:\:−\:\:\int\:{v}\:\:{du}\:\:=\:\:\:\left(\mathrm{5}{x}\:.\:\:\frac{\mathrm{5}}{\mathrm{4}}\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} \right)\:\:−\:\:\int\:\:\frac{\mathrm{5}}{\mathrm{4}}\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} \:\left(\mathrm{5}\:{dx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{25}{x}}{\mathrm{4}}\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} \:\:−\:\:\left(\frac{\mathrm{5}×\mathrm{5}}{\mathrm{4}×\mathrm{4}}\:{e}\:^{\frac{\mathrm{4}{x}}{\mathrm{5}}} .\:\mathrm{5}\right)\:\:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{25}\:{e}^{\frac{\mathrm{4}{x}}{\mathrm{5}}} }{\mathrm{4}}\:\left(\:{x}\:−\:\frac{\mathrm{5}}{\mathrm{4}}\right)\:\:+\:\:{C} \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

7)∫2x^3 e^(−(x/3)) dx 2x^3 ∫e^(−(x/3)) dx−∫[(d/dx)(2x^3 )∫e^(−(x/3)) dx]dx =2x^3 ×(e^((−x)/3) /((−1)/3))−∫6x^2 ×(e^(−(x/3)) /((−1)/3))dx =−6x^3 e^((−x)/3) +18I_2 I_2 =∫x^2 e^((−x)/3) dx =x^2 ×(e^((−x)/3) /((−1)/3))−∫[(dx^2 /dx)∫e^((−x)/3) dx]dx =−3x^2 e^((−x)/3) −∫2x×(e^((−x)/3) /((−1)/3))dx =−3x^2 e^((−x)/3) +6∫xe^((−x)/3) dx =−3x^2 e^((−x)/3) +6I_3 I_3 =∫xe^((−x)/3) dx =x×(e^(−(x/3)) /((−1)/3))−∫[(dx/dx)∫e^((−x)/3) dx]dx =((−3xe^((−x)/3) )/1)−∫(e^((−x)/3) /((−1)/3))dx =((−3xe^((−x)/3) )/1)+3×(e^((−x)/3) /((−1)/3))+C =−3xe^((−x)/3) −9e^(−(x/3)) +C pls do rest by putting I_2 and I_3

$$\left.\mathrm{7}\right)\int\mathrm{2}{x}^{\mathrm{3}} {e}^{−\frac{{x}}{\mathrm{3}}} {dx} \\ $$$$\mathrm{2}{x}^{\mathrm{3}} \int{e}^{−\frac{{x}}{\mathrm{3}}} {dx}−\int\left[\frac{{d}}{{dx}}\left(\mathrm{2}{x}^{\mathrm{3}} \right)\int{e}^{−\frac{{x}}{\mathrm{3}}} {dx}\right]{dx} \\ $$$$=\mathrm{2}{x}^{\mathrm{3}} ×\frac{{e}^{\frac{−{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}−\int\mathrm{6}{x}^{\mathrm{2}} ×\frac{{e}^{−\frac{{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}{dx} \\ $$$$=−\mathrm{6}{x}^{\mathrm{3}} {e}^{\frac{−{x}}{\mathrm{3}}} +\mathrm{18}{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\int{x}^{\mathrm{2}} {e}^{\frac{−{x}}{\mathrm{3}}} {dx} \\ $$$$={x}^{\mathrm{2}} ×\frac{{e}^{\frac{−{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}−\int\left[\frac{{dx}^{\mathrm{2}} }{{dx}}\int{e}^{\frac{−{x}}{\mathrm{3}}} {dx}\right]{dx} \\ $$$$=−\mathrm{3}{x}^{\mathrm{2}} {e}^{\frac{−{x}}{\mathrm{3}}} −\int\mathrm{2}{x}×\frac{{e}^{\frac{−{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}{dx} \\ $$$$=−\mathrm{3}{x}^{\mathrm{2}} {e}^{\frac{−{x}}{\mathrm{3}}} +\mathrm{6}\int{xe}^{\frac{−{x}}{\mathrm{3}}} {dx} \\ $$$$=−\mathrm{3}{x}^{\mathrm{2}} {e}^{\frac{−{x}}{\mathrm{3}}} +\mathrm{6}{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{3}} =\int{xe}^{\frac{−{x}}{\mathrm{3}}} \:{dx} \\ $$$$={x}×\frac{{e}^{−\frac{{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}−\int\left[\frac{{dx}}{{dx}}\int{e}^{\frac{−{x}}{\mathrm{3}}} {dx}\right]{dx} \\ $$$$=\frac{−\mathrm{3}{xe}^{\frac{−{x}}{\mathrm{3}}} }{\mathrm{1}}−\int\frac{{e}^{\frac{−{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}{dx} \\ $$$$=\frac{−\mathrm{3}{xe}^{\frac{−{x}}{\mathrm{3}}} }{\mathrm{1}}+\mathrm{3}×\frac{{e}^{\frac{−{x}}{\mathrm{3}}} }{\frac{−\mathrm{1}}{\mathrm{3}}}+{C} \\ $$$$=−\mathrm{3}{xe}^{\frac{−{x}}{\mathrm{3}}} −\mathrm{9}{e}^{−\frac{{x}}{\mathrm{3}}} +{C} \\ $$$${pls}\:{do}\:{rest}\:{by}\:{putting}\:{I}_{\mathrm{2}} {and}\:{I}_{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com