The distances from a point to the sides of a triangle are p,q,r. Find the maximum (or minimum) area of the triangle, if it exists. Assume r≤q≤p.


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 50352 by mr W last updated on 16/Dec/18

$T h e d i s t a n c e s f r o m a p o i n t t o t h e s i d e s$ $o f a t r i a n g l e a r e p, q, r . F i n d t h e$ $m a x i m u m (o r m i n i m u m) a r e a o f t h e$ $t r i a n g l e, i f i t e x i s t s .$ $A s s u m e r ⩽ q ⩽ p .$
Commented by ajfour last updated on 16/Dec/18

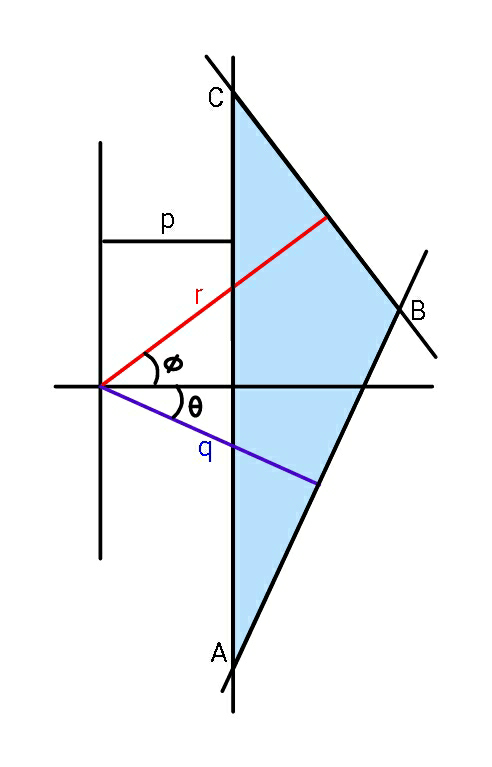
Commented by ajfour last updated on 17/Dec/18

$D [r \cos θ - p \cos (θ + ϕ)] = N \sin ϕ \sin (2 θ + ϕ)$ $x \cos θ - y \sin θ = q$ $e q . o f B C$ $x \cos ϕ + y \sin ϕ = r$ $y_{C} = \frac{r - p \cos ϕ}{\sin ϕ}, y_{A} = \frac{p \cos θ - q}{\sin θ}$ $x_{B} = \frac{q \sin ϕ + r \sin θ}{\sin (θ + ϕ)}$ $△ = (\frac{x_{B} - p}{2}) (y_{C} - y_{A})$ $= [\frac{q \sin ϕ + r \sin θ - p \sin (θ + ϕ)}{2 \sin (θ + ϕ)}]$ $\times [\frac{q \sin ϕ + r \sin θ - p \sin (θ + ϕ)}{\sin θ \sin ϕ}]$ $___________________________$ $△ = \frac{{[q \sin ϕ + r \sin θ - p \sin (θ + ϕ)]}^{2}}{2 \sin (θ + ϕ) \sin θ \sin ϕ}$ $___________________________$
Commented by ajfour last updated on 16/Dec/18

$y e s S i r, b u t s t i l l n o t a n e a s y g o i n g . .$
Commented by mr W last updated on 16/Dec/18

$i t i s i n d e e d n o t e a s y .$
Commented by mr W last updated on 17/Dec/18

$t h a n k y o u s i r f o r t h e w o r k i n g!$ $i^{'} m s t i l l t h i n k i n g a b o u t t h i s q u e s t i o n .$ $w e c a n s e e i n t h i s d i a g r a m :$ $w h e n θ a n d ϕ \to π / 2, Δ \to \infty$ $a n d w h e n θ a n d ϕ \to 0, Δ \to \infty$ $d o e s i t n o t m e a n t h a t a m i n i n m u m$ $f o r Δ s h o u l d e x i s t ?$
	Answered by mr W last updated on 16/Dec/18

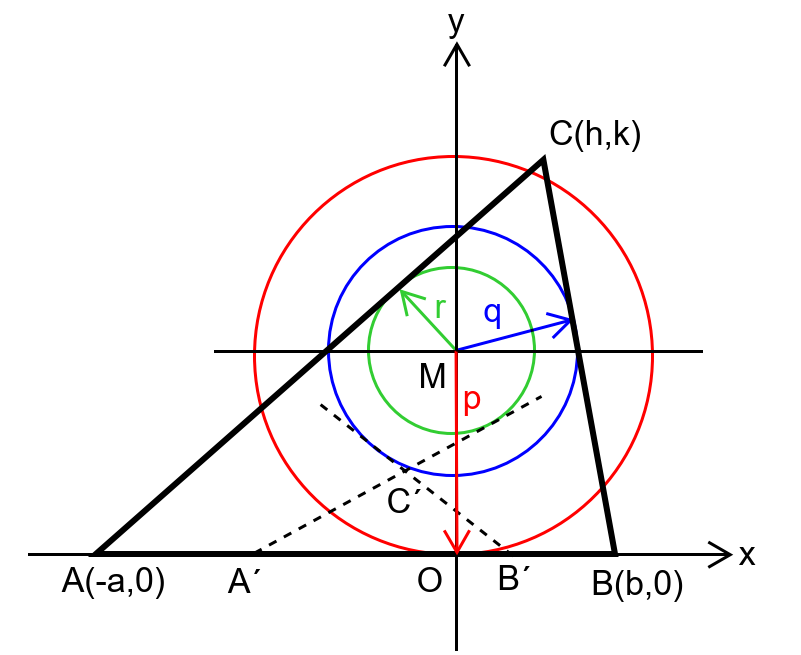
	Commented by mr W last updated on 16/Dec/18

	$d r a w t h r e e c i r c l e s f r o m t h e s a m e c e n t e r$ $w i t h r a d i i p, q, r .$ $i t i s t o f i n d a t r i a n g l e w h o s e s i d e s$ $t a n g e n t t h e s e t h r e e c i r c l e s a n d h a s$ $m a x i m u m a r e a (l i k e Δ A B C) o r$ $m i n i m u m a r e a (l i k e Δ A^{'} B^{'} C^{'}) .$ $A (- a, 0) a n d B (b, 0) a n d C (h, k) .$ $E q n . o f A C :$ $\frac{y}{k} = \frac{x + a}{h + a}$ $\Rightarrow \frac{k}{h + a} x - y + \frac{a k}{h + a} = 0$ $E q n . o f c i r c l e w i t h r a d i u s r :$ $x^{2} + {(y - p)}^{2} = r^{2}$ $A C i s t a n g e n t,$ $\Rightarrow {(\frac{k}{h + a})}^{2} r^{2} + r^{2} = {(- p + \frac{a k}{h + a})}^{2} = p^{2} - 2 p a (\frac{k}{h + a}) + a^{2} {(\frac{k}{h + a})}^{2}$ $\Rightarrow (a^{2} - r^{2}) {(\frac{k}{h + a})}^{2} - 2 p a (\frac{k}{h + a}) + (p^{2} - r^{2}) = 0$ $\Rightarrow \frac{k}{h + a} = \frac{p a \pm \sqrt{p^{2} a^{2} - (a^{2} - r^{2}) (p^{2} - r^{2})}}{a^{2} - r^{2}} = \frac{p a \pm r \sqrt{p^{2} - r^{2} + a^{2}}}{a^{2} - r^{2}}$ $w e c o n s i d e r a t f i r s t t h e b i g t r i a n g l e,$ $\Rightarrow \frac{k}{h + a} = \frac{p a + r \sqrt{p^{2} - r^{2} + a^{2}}}{a^{2} - r^{2}}$ $\Rightarrow h = \frac{a^{2} - r^{2}}{p a + r \sqrt{p^{2} - r^{2} + a^{2}}} k - a$ $E q n . o f B C :$ $\frac{y}{k} = \frac{x - b}{h - b}$ $\Rightarrow \frac{k}{h - b} x - y - \frac{b k}{h - b} = 0$ $E q n . o f c i r c l e w i t h r a d i u s q :$ $x^{2} + {(y - p)}^{2} = q^{2}$ $B C i s t a n g e n t,$ $\Rightarrow {(\frac{k}{h - b})}^{2} q^{2} + q^{2} = {(- p - \frac{b k}{h - b})}^{2} = p^{2} + 2 p b (\frac{k}{h - b}) + b^{2} {(\frac{k}{h - b})}^{2}$ $\Rightarrow (b^{2} - q^{2}) {(\frac{k}{h - b})}^{2} + 2 p b (\frac{k}{h - b}) + (p^{2} - q^{2}) = 0$ $\Rightarrow \frac{k}{h - b} = \frac{- p b + q \sqrt{p^{2} - q^{2} + b^{2}}}{b^{2} - q^{2}}$ $\Rightarrow h = \frac{b^{2} - q^{2}}{- p b + q \sqrt{p^{2} - q^{2} + b^{2}}} k + b$ $\Rightarrow \frac{a^{2} - r^{2}}{p a + r \sqrt{p^{2} - r^{2} + a^{2}}} k - a = \frac{b^{2} - q^{2}}{- p b + q \sqrt{p^{2} - q^{2} + b^{2}}} k + b$ $\Rightarrow [\frac{a^{2} - r^{2}}{p a + r \sqrt{p^{2} - r^{2} + a^{2}}} - \frac{b^{2} - q^{2}}{- p b + q \sqrt{p^{2} - q^{2} + b^{2}}}] k = a + b$ $\Rightarrow k = \frac{a + b}{\frac{a^{2} - r^{2}}{p a + r \sqrt{p^{2} - r^{2} + a^{2}}} - \frac{b^{2} - q^{2}}{- p b + q \sqrt{p^{2} - q^{2} + b^{2}}}}$ $a r e a o f Δ A B C$ $Δ = \frac{1}{2} (a + b) k$ $\Rightarrow Δ = \frac{1}{2} \times \frac{{(a + b)}^{2}}{\frac{a^{2} - r^{2}}{p a + r \sqrt{p^{2} - r^{2} + a^{2}}} - \frac{b^{2} - q^{2}}{- p b + q \sqrt{p^{2} - q^{2} + b^{2}}}}$ $\frac{\partial Δ}{\partial a} = \frac{\partial Δ}{\partial b} = 0$ $. . . . . .$
	Commented by mr W last updated on 17/Dec/18

	${y o u}^{'} r e r i g h t .$ $x \to 0, y \to 0 \Rightarrow Δ \to 0$ $x \to \infty, y \to \infty \Rightarrow Δ \to \infty$ $I t h o u g h t t h e r e i s a m i n i m u m f o r$ $Δ A B C a n d a m a x i m u m f o r Δ A^{'} B^{'} C^{'} .$ $b u t t h i s i s n o t t r u e . s o t h i s i s n o t a$ $g o o d q u e s t i o n . t h a n k s f o r t r y i n g a n d$ $f o r t h e c o r r e c t c o n c l u s i o n .$
	Commented by ajfour last updated on 17/Dec/18

	$b u t i t h i n k m i n i m u m i s z e r o$ $a n d m a x i m u m \to \infty .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum