
Question and Answers Forum
Question Number 50412 by Abdo msup. last updated on 16/Dec/18
![1) calculate U_n =∫_0 ^π (dx/(1+cos^2 (nx))) with n from N 2) f continue from [0,π] to R find lim_(n→+∞) ∫_0 ^π ((f(x))/(1+cos^2 (nx)))dx](Q50412.png)
Commented by Abdo msup. last updated on 25/Dec/18
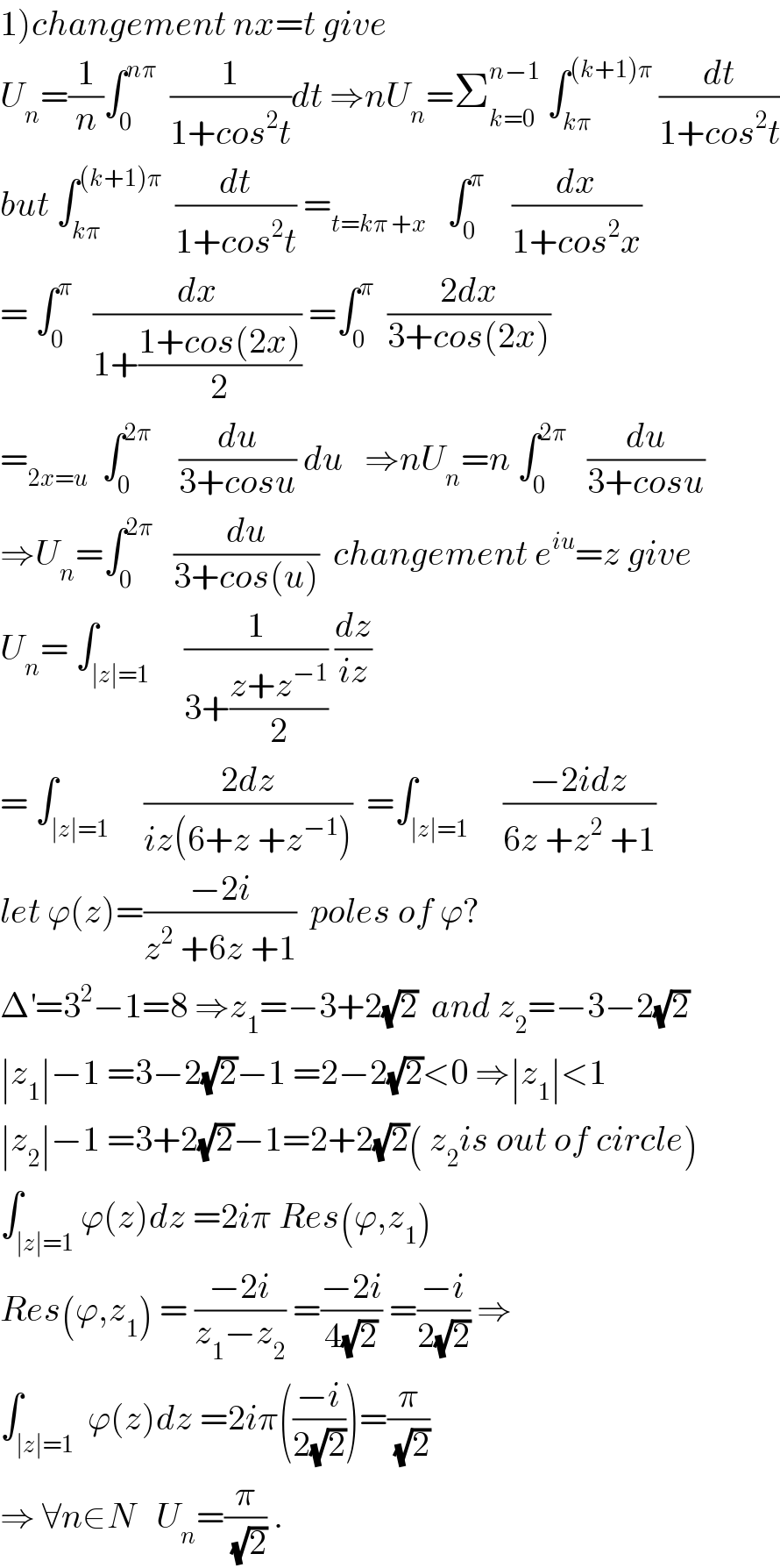
| ||
Question and Answers Forum | ||
Question Number 50412 by Abdo msup. last updated on 16/Dec/18 | ||
![1) calculate U_n =∫_0 ^π (dx/(1+cos^2 (nx))) with n from N 2) f continue from [0,π] to R find lim_(n→+∞) ∫_0 ^π ((f(x))/(1+cos^2 (nx)))dx](Q50412.png) | ||
Commented by Abdo msup. last updated on 25/Dec/18 | ||
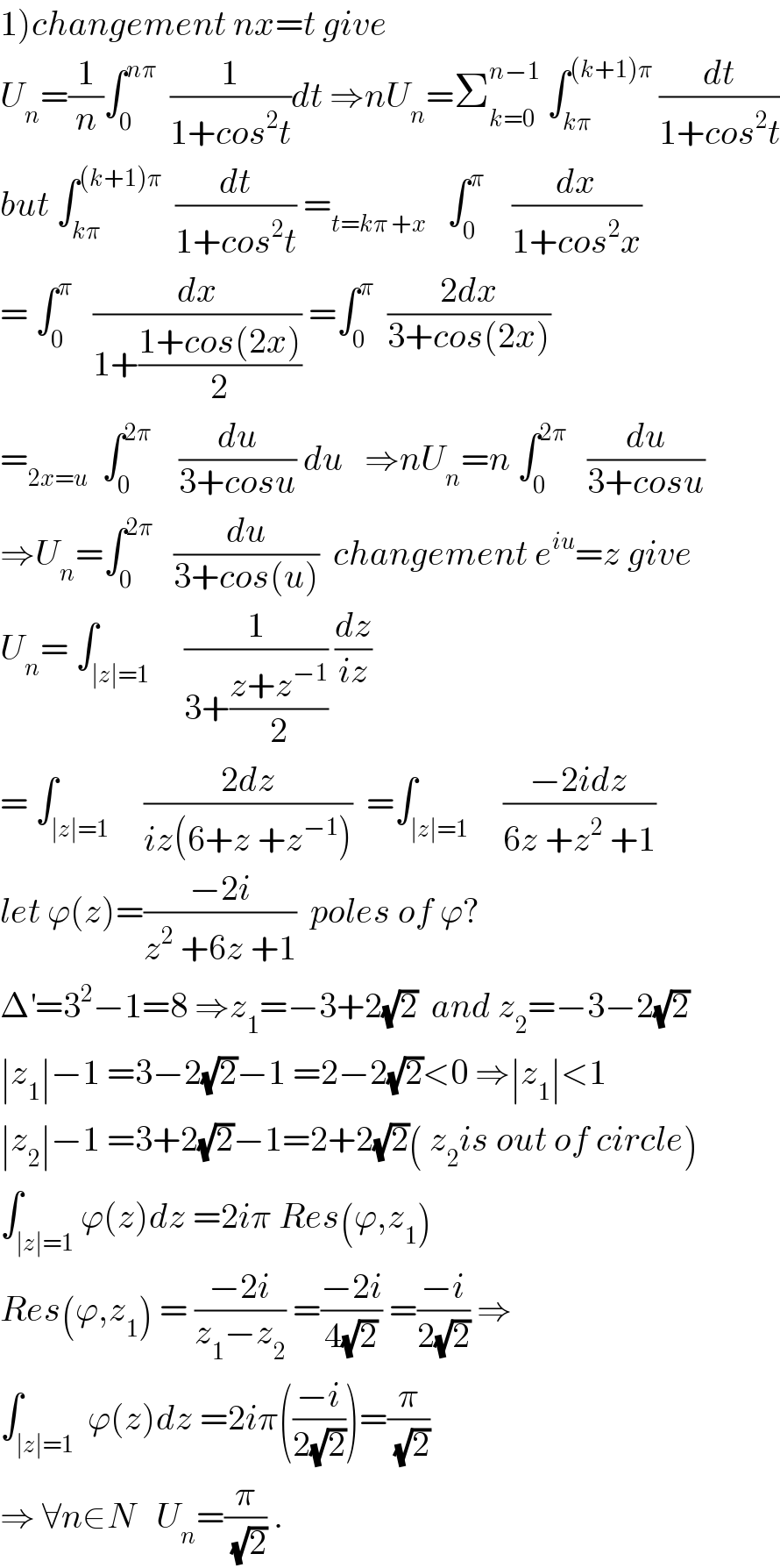 | ||