
Question and Answers Forum
Question Number 50413 by Abdo msup. last updated on 16/Dec/18
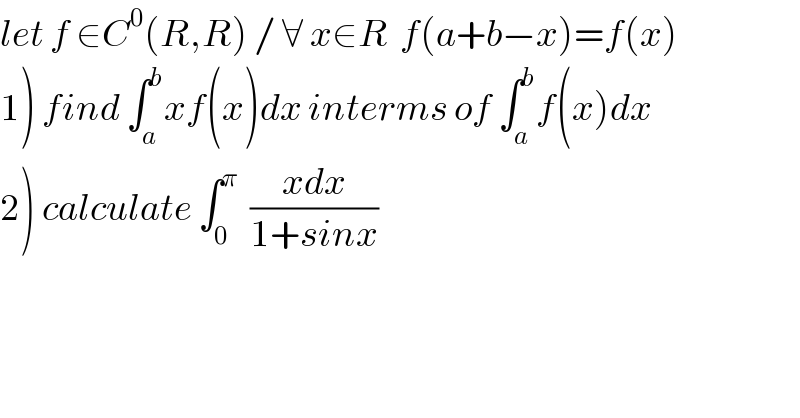
Commented by Abdo msup. last updated on 24/Dec/18
![1)∫_a ^b xf(x)dx =∫_a ^b xf(a+b−x)dx =_(a+b−x=t ) −∫_b ^a (a+b−t)f(t)dt =∫_a ^b (a+b)f(t) −∫_a ^b tf(t)dt ⇒ 2 ∫_a ^b xf(x)dx =(a+b)∫_a ^b f(t)dt ⇒ ∫_a ^b xf(x)dx =((a+b)/2) ∫_a ^b f(x)dx 2) we have ∫_0 ^π ((xdx)/(1+sinx)) =∫_0 ^π xf(x)dx with f(x)=(1/(1+sinx)) we have f(0+π−x)=(1/(1+sin(π−x))) =f(x) ⇒∫_0 ^π xf(x)dx =(π/2) ∫_0 ^π (dx/(1+sinx)) =_(tan((x/2))=t) (π/2) ∫_0 ^∞ (1/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =π ∫_0 ^∞ (dt/(1+t^2 +2t)) =π ∫_0 ^∞ (dt/((t+1)^2 )) =π [−(1/(t+1))]_0 ^(+∞) = π .](Q51145.png)
| ||
Question and Answers Forum | ||
Question Number 50413 by Abdo msup. last updated on 16/Dec/18 | ||
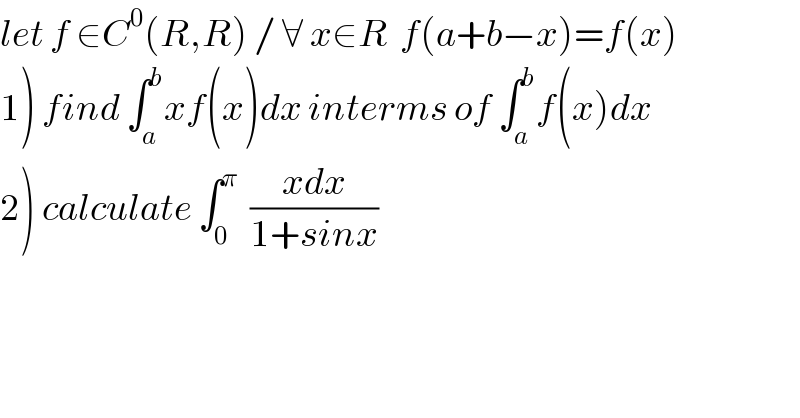 | ||
Commented by Abdo msup. last updated on 24/Dec/18 | ||
![1)∫_a ^b xf(x)dx =∫_a ^b xf(a+b−x)dx =_(a+b−x=t ) −∫_b ^a (a+b−t)f(t)dt =∫_a ^b (a+b)f(t) −∫_a ^b tf(t)dt ⇒ 2 ∫_a ^b xf(x)dx =(a+b)∫_a ^b f(t)dt ⇒ ∫_a ^b xf(x)dx =((a+b)/2) ∫_a ^b f(x)dx 2) we have ∫_0 ^π ((xdx)/(1+sinx)) =∫_0 ^π xf(x)dx with f(x)=(1/(1+sinx)) we have f(0+π−x)=(1/(1+sin(π−x))) =f(x) ⇒∫_0 ^π xf(x)dx =(π/2) ∫_0 ^π (dx/(1+sinx)) =_(tan((x/2))=t) (π/2) ∫_0 ^∞ (1/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =π ∫_0 ^∞ (dt/(1+t^2 +2t)) =π ∫_0 ^∞ (dt/((t+1)^2 )) =π [−(1/(t+1))]_0 ^(+∞) = π .](Q51145.png) | ||