
Question and Answers Forum
Question Number 50422 by Abdo msup. last updated on 16/Dec/18
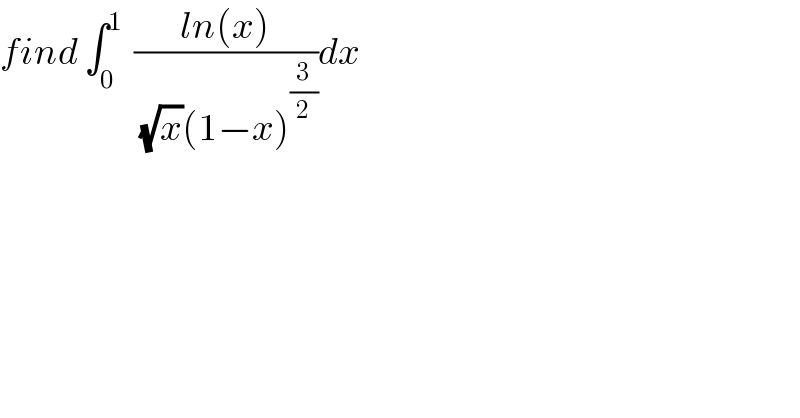
Commented by Abdo msup. last updated on 23/Dec/18
![changement x =sin^2 θ give ∫_0 ^1 ((ln(x))/((√x)(1−x)^(3/2) ))dx =∫_0 ^(π/2) ((2ln(sinθ))/(sinθ(cos^2 θ)^(3/2) )) 2sinθ cosθ dθ =4∫_0 ^(π/2) ((ln(sinθ))/(cos^2 θ)) dθ by psrts u^′ =(1/(cos^2 θ)) and v=ln(sinθ) =4 { [tanθ ln(sinθ)]_0 ^(π/2) −∫_0 ^(π/2) tanθ ((cosθ)/(sinθ))dθ} =−4 ∫_0 ^(π/2) dθ =−2π .rest to prove that lim_(θ→0) tanθ ln(sinθ)=0 and lim_(θ→(π/2)) tanθ ln(sinθ)=0 for x∈v(0) tanθ∼ θ ,ln(sinθ)∼ln(θ) ⇒ tanθ ln(sinθ)∼θ lnθ →0 (θ→0) ch. θ =(π/2)−t give tanθ ln(sinθ) =tan((π/2)−t)ln(cost) =((ln(cost))/(tan(t))) but cost ∼ 1−(t^2 /2) and ln(cost)∼−(t^2 /2) tan(t)∼ t ⇒((ln(cost))/(tan(t))) ∼ −(t/2) →0(t→0) ⇒the result is proved.](Q51067.png)
Answered by Smail last updated on 27/Dec/18
![by parts u=lnx⇒u′=(1/x) v′=(1/((√x)(1−x)^(3/2) ))⇒v=((2(√x))/(√(1−x))) I=∫_0 ^1 ((lnx)/((√x)(1−x)^(3/2) ))dx=2[(((√x)lnx)/(√(1−x)))]_0 ^1 −2∫_0 ^1 (dx/((√x)(√(1−x)))) let t^2 =x⇒2tdt=dx I=0−4∫_0 ^1 ((tdt)/(t(√(1−t^2 )))) =−4[sin^(−1) t]_0 ^1 =−4((π/2)+2kπ−kπ) =−4((π/2)+kπ)](Q51453.png)
| ||
Question and Answers Forum | ||
Question Number 50422 by Abdo msup. last updated on 16/Dec/18 | ||
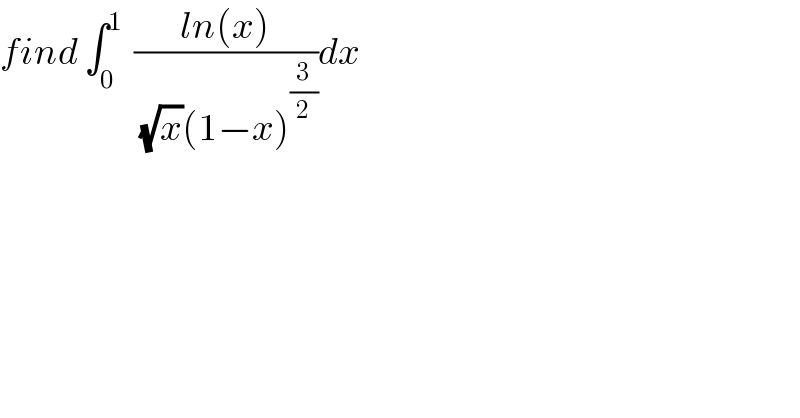 | ||
Commented by Abdo msup. last updated on 23/Dec/18 | ||
![changement x =sin^2 θ give ∫_0 ^1 ((ln(x))/((√x)(1−x)^(3/2) ))dx =∫_0 ^(π/2) ((2ln(sinθ))/(sinθ(cos^2 θ)^(3/2) )) 2sinθ cosθ dθ =4∫_0 ^(π/2) ((ln(sinθ))/(cos^2 θ)) dθ by psrts u^′ =(1/(cos^2 θ)) and v=ln(sinθ) =4 { [tanθ ln(sinθ)]_0 ^(π/2) −∫_0 ^(π/2) tanθ ((cosθ)/(sinθ))dθ} =−4 ∫_0 ^(π/2) dθ =−2π .rest to prove that lim_(θ→0) tanθ ln(sinθ)=0 and lim_(θ→(π/2)) tanθ ln(sinθ)=0 for x∈v(0) tanθ∼ θ ,ln(sinθ)∼ln(θ) ⇒ tanθ ln(sinθ)∼θ lnθ →0 (θ→0) ch. θ =(π/2)−t give tanθ ln(sinθ) =tan((π/2)−t)ln(cost) =((ln(cost))/(tan(t))) but cost ∼ 1−(t^2 /2) and ln(cost)∼−(t^2 /2) tan(t)∼ t ⇒((ln(cost))/(tan(t))) ∼ −(t/2) →0(t→0) ⇒the result is proved.](Q51067.png) | ||
Answered by Smail last updated on 27/Dec/18 | ||
![by parts u=lnx⇒u′=(1/x) v′=(1/((√x)(1−x)^(3/2) ))⇒v=((2(√x))/(√(1−x))) I=∫_0 ^1 ((lnx)/((√x)(1−x)^(3/2) ))dx=2[(((√x)lnx)/(√(1−x)))]_0 ^1 −2∫_0 ^1 (dx/((√x)(√(1−x)))) let t^2 =x⇒2tdt=dx I=0−4∫_0 ^1 ((tdt)/(t(√(1−t^2 )))) =−4[sin^(−1) t]_0 ^1 =−4((π/2)+2kπ−kπ) =−4((π/2)+kπ)](Q51453.png) | ||
| ||