Question Number 50423 by Abdo msup. last updated on 16/Dec/18
$${find}\:{f}\left({a}\right)\:=\int_{{a}} ^{+\infty} \:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}\:\:{with}\:{a}>\mathrm{0} \\ $$
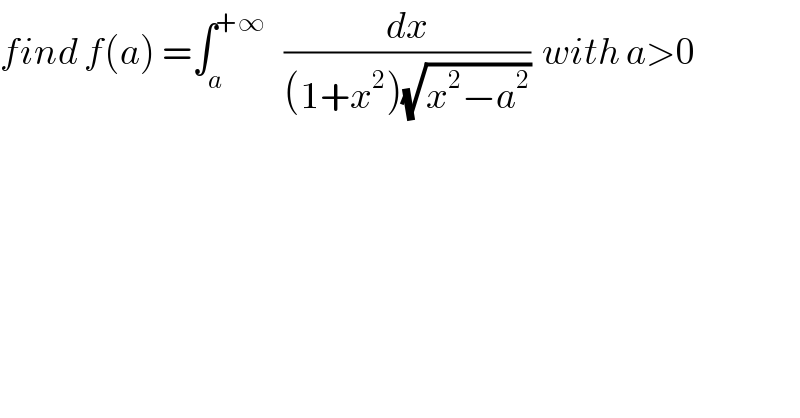
Commented byAbdo msup. last updated on 17/Dec/18
![changement x=ach(t) give t=argch((x/a)) f(a) = ∫_0 ^(+∞) ((ash(t)dt)/((1+a^2 ch^2 (t))ash(t))) =∫_0 ^∞ (dt/(1+a^2 ((1+ch(2t))/2))) =∫_0 ^∞ ((2dt)/(2 +a^2 +a^2 ((e^(2t) +e^(−2t) )/2))) = ∫_0 ^∞ ((4dt)/(4 +2a^2 +a^2 e^(2t) +a^2 e^(−2t) )) =_(e^(2t) =u) ∫_1 ^∞ (4/(4+2a^2 +a^2 u +a^2 u^(−1) )) (du/(2u)) =2∫_1 ^∞ (du/((4+2a^2 )u +a^2 u^2 +a^2 )) =∫_1 ^∞ ((2du)/(a^2 u^2 +(4+2a^2 )u +a^2 )) Δ^′ =(2+a^2 )^2 −a^4 =4+4a^2 >0 ⇒ u_1 =((−2−a^2 +2(√(1+a^2 )))/a^2 ) u_2 =((−2−a^2 −2(√(1+a^2 )))/a^2 ) F(u)=(2/((u−u_1 )(u−u_2 ))) =(2/(u_1 −u_2 ))((1/(u−u_1 )) −(1/(u−u_2 ))) =(a^2 /(2(√(1+a^2 ))))((1/(u−u_1 )) −(1/(u−u_2 ))) ⇒ ∫_1 ^∞ F(u)du =(a^2 /(2(√(1+a^2 ))))[ln∣((u−u_1 )/(u−u_2 ))∣]_1 ^(+∞) =(a^2 /(2(√(1+a^2 ))))ln∣((1−u_2 )/(1−u_1 ))∣ =(a^2 /(2(√(1+a^2 ))))ln∣((1−((−2−a^2 −2(√(1+a^2 )))/a^2 ))/(1−((−2−a^2 +2(√(1+a^2 )))/a^2 )))∣ =(a^2 /(2(√(1+a^2 ))))ln∣((2a^2 +2+2(√(1+a^2 )))/(2a^2 +2−2(√(1+a^2 ))))∣ =(a^2 /(2(√(1+a^2 ))))ln∣((a^2 +1+(√(1+a^2 )))/(a^2 +1−(√(1+a^2 ))))∣ =f(a)](Q50613.png)
$${changement}\:{x}={ach}\left({t}\right)\:{give}\:{t}={argch}\left(\frac{{x}}{{a}}\right) \\ $$ $${f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{ash}\left({t}\right){dt}}{\left(\mathrm{1}+{a}^{\mathrm{2}} {ch}^{\mathrm{2}} \left({t}\right)\right){ash}\left({t}\right)} \\ $$ $$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{a}^{\mathrm{2}} \:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{\mathrm{2}\:+{a}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}} \\ $$ $$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{4}{dt}}{\mathrm{4}\:+\mathrm{2}{a}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \:{e}^{\mathrm{2}{t}} \:+{a}^{\mathrm{2}} {e}^{−\mathrm{2}{t}} } \\ $$ $$=_{{e}^{\mathrm{2}{t}} \:={u}} \:\:\:\int_{\mathrm{1}} ^{\infty} \:\:\:\:\:\:\:\frac{\mathrm{4}}{\mathrm{4}+\mathrm{2}{a}^{\mathrm{2}} \:+{a}^{\mathrm{2}} {u}\:+{a}^{\mathrm{2}} {u}^{−\mathrm{1}} }\:\frac{{du}}{\mathrm{2}{u}} \\ $$ $$=\mathrm{2}\int_{\mathrm{1}} ^{\infty} \:\:\:\:\:\frac{{du}}{\left(\mathrm{4}+\mathrm{2}{a}^{\mathrm{2}} \right){u}\:+{a}^{\mathrm{2}} {u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$ $$=\int_{\mathrm{1}} ^{\infty} \:\:\:\:\:\frac{\mathrm{2}{du}}{{a}^{\mathrm{2}} {u}^{\mathrm{2}} \:+\left(\mathrm{4}+\mathrm{2}{a}^{\mathrm{2}} \right){u}\:+{a}^{\mathrm{2}} } \\ $$ $$\Delta^{'} =\left(\mathrm{2}+{a}^{\mathrm{2}} \right)^{\mathrm{2}} −{a}^{\mathrm{4}} =\mathrm{4}+\mathrm{4}{a}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow \\ $$ $${u}_{\mathrm{1}} =\frac{−\mathrm{2}−{a}^{\mathrm{2}} \:+\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} } \\ $$ $${u}_{\mathrm{2}} =\frac{−\mathrm{2}−{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} } \\ $$ $${F}\left({u}\right)=\frac{\mathrm{2}}{\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)}\:=\frac{\mathrm{2}}{{u}_{\mathrm{1}} −{u}_{\mathrm{2}} }\left(\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right) \\ $$ $$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\left(\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right)\:\Rightarrow \\ $$ $$\int_{\mathrm{1}} ^{\infty} \:\:{F}\left({u}\right){du}\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\left[{ln}\mid\frac{{u}−{u}_{\mathrm{1}} }{{u}−{u}_{\mathrm{2}} }\mid\right]_{\mathrm{1}} ^{+\infty} \\ $$ $$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\mid\frac{\mathrm{1}−{u}_{\mathrm{2}} }{\mathrm{1}−{u}_{\mathrm{1}} }\mid\: \\ $$ $$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\mid\frac{\mathrm{1}−\frac{−\mathrm{2}−{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} }}{\mathrm{1}−\frac{−\mathrm{2}−{a}^{\mathrm{2}} \:+\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} }}\mid \\ $$ $$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\mid\frac{\mathrm{2}{a}^{\mathrm{2}} \:+\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{\mathrm{2}{a}^{\mathrm{2}} \:+\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\mid \\ $$ $$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\mid\frac{{a}^{\mathrm{2}} \:+\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} \:+\mathrm{1}−\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\mid\:={f}\left({a}\right) \\ $$ $$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
![∫(dx/((1+x^2 )(√(x^2 −a^2 )))) t=(1/x) x=(1/t) dx=((−1)/t^2 )dt ∫((−dt)/(t^2 (1+(1/t^2 ))(√((1/t^2 )−a^2 )) )) ∫((−tdt)/((t^2 +1)(√(1−a^2 t^2 )))) =((−1)/a)∫((tdt)/((t^2 +1)(√((1/a^2 )−t^2 )) )) k=t^2 dk=2tdt =((−1)/(2a))∫(dk/((k+1)(√((1/a^2 )−k)))) p^2 =(1/a^2 )−k 2pdp=−dk =((−1)/(2a))∫((−2pdp)/(((1/a^2 )−p^2 +1)p)) =(1/a)∫(dp/(((1/a^2 )+1)−p^2 )) formula[ ∫(dx/(a^2 −x^2 ))=(1/(2a))ln(((a+x)/(a−x)))] =(1/a)×(1/(2(√(((1/a^2 )+1))) ))×ln((((√((1/a^2 )+1)) +p)/((√((1/a^2 )+1)) −p))) =(1/(2(√(1+a^2 ))))ln((((√((1/a^2 )+1)) +(√((1/a^2 )−k)) )/((√((1/a^2 )+1)) −(√((1/a^2 )−k)) ))) =(1/(2(√(1+a^2 ))))ln((((√(1+a^2 )) +(√(1−a^2 k)) )/((√(1+a^2 )) −(√(1−a^2 k))))) =(1/(2(√(1+a^2 ))))ln((((√(1+a^2 )) +(√(1−a^2 t^2 )))/((√(1+a^2 )) −(√(1−a^2 t^2 )) ))) =(1/(2(√(1+a^2 ))))∣ln((((√(1+a^2 )) +(√(1−(a^2 /x^2 ))))/((√(1+a^2 )) −(√(1−(a^2 /x^2 ))))))∣_a ^∞ =(1/(2(√(1+a^2 ))))[{ln((((√(1+a^2 )) +(√(1−0)))/((√(1+a^2 )) −(√(1−0)))))}−ln((((√(1+a^2 )) +(√0))/((√(1+a^2 )) −(√0))))}] =(1/(√(1+a^2 )))ln((((√(1+a^2 )) +1)/((√(1+a^2 )) −1)))](Q50537.png)
$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }} \\ $$ $${t}=\frac{\mathrm{1}}{{x}}\:\:{x}=\frac{\mathrm{1}}{{t}}\:\:{dx}=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$ $$\int\frac{−{dt}}{{t}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−{a}^{\mathrm{2}} }\:} \\ $$ $$\int\frac{−{tdt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{1}−{a}^{\mathrm{2}} {t}^{\mathrm{2}} }} \\ $$ $$=\frac{−\mathrm{1}}{{a}}\int\frac{{tdt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−{t}^{\mathrm{2}} }\:} \\ $$ $${k}={t}^{\mathrm{2}} \:\:{dk}=\mathrm{2}{tdt} \\ $$ $$=\frac{−\mathrm{1}}{\mathrm{2}{a}}\int\frac{{dk}}{\left({k}+\mathrm{1}\right)\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−{k}}} \\ $$ $${p}^{\mathrm{2}} =\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−{k}\:\:\:\:\mathrm{2}{pdp}=−{dk} \\ $$ $$=\frac{−\mathrm{1}}{\mathrm{2}{a}}\int\frac{−\mathrm{2}{pdp}}{\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−{p}^{\mathrm{2}} +\mathrm{1}\right){p}} \\ $$ $$=\frac{\mathrm{1}}{{a}}\int\frac{{dp}}{\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}\right)−{p}^{\mathrm{2}} }\:{formula}\left[\:\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\left(\frac{{a}+{x}}{{a}−{x}}\right)\right] \\ $$ $$=\frac{\mathrm{1}}{{a}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}\right)}\:}×{ln}\left(\frac{\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}}\:+{p}}{\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}}\:−{p}}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\left(\frac{\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}}\:+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−{k}}\:}{\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}}\:−\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−{k}}\:}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\left(\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}−{a}^{\mathrm{2}} {k}}\:}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:−\sqrt{\mathrm{1}−{a}^{\mathrm{2}} {k}}}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\left(\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}−{a}^{\mathrm{2}} {t}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:−\sqrt{\mathrm{1}−{a}^{\mathrm{2}} {t}^{\mathrm{2}} }\:}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\mid{ln}\left(\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:−\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}}\right)\mid_{{a}} ^{\infty} \\ $$ $$\left.=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\left[\left\{{ln}\left(\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}−\mathrm{0}}}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:−\sqrt{\mathrm{1}−\mathrm{0}}}\right)\right\}−{ln}\left(\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:+\sqrt{\mathrm{0}}}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:−\sqrt{\mathrm{0}}}\right)\right\}\right] \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{ln}\left(\frac{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:+\mathrm{1}}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:−\mathrm{1}}\right) \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$
Commented byAbdo msup. last updated on 17/Dec/18
$${thank}\:{you}\:{sir}\:{tanmay}. \\ $$