Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 50426 by Abdo msup. last updated on 16/Dec/18

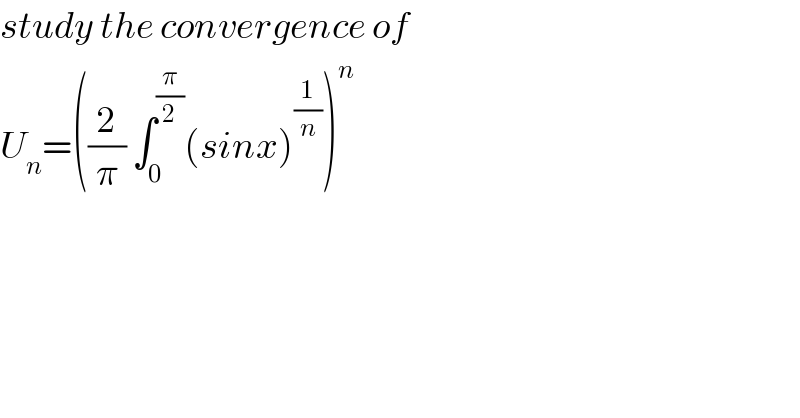
study the convergence of U_n =((2/π) ∫_0 ^(π/2) (sinx)^(1/n) )^n

$${study}\:{the}\:{convergence}\:{of}\: \\ $$$${U}_{{n}} =\left(\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sinx}\right)^{\frac{\mathrm{1}}{{n}}} \right)^{{n}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

(1/π)×2∫_0 ^(π/2) sinx)^(2×(((1+n)/(2n)))−1) (cosx)^(2×(1/2)−1) dx formula 2∫_0 ^(π/2) sin^(2p−1) xcos^(2q−1) xdx =((⌈(p)⌈q))/(⌈p+q))) so (1/π)×((⌈(((1+n)/(2n)))×⌈((1/2)))/(⌈(((1+n)/(2n))+(1/2)))) =(1/(√π))×((⌈((1/(2n))+(1/2)))/(⌈((1/(2n))+1))) wait...

$$\left.\frac{\mathrm{1}}{\pi}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sinx}\right)^{\mathrm{2}×\left(\frac{\mathrm{1}+{n}}{\mathrm{2}{n}}\right)−\mathrm{1}} \left({cosx}\right)^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dx} \\ $$$${formula}\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{p}−\mathrm{1}} {xcos}^{\mathrm{2}{q}−\mathrm{1}} {xdx} \\ $$$$=\frac{\left.\lceil\left({p}\right)\lceil{q}\right)}{\left.\lceil{p}+{q}\right)} \\ $$$${so}\:\frac{\mathrm{1}}{\pi}×\frac{\lceil\left(\frac{\mathrm{1}+{n}}{\mathrm{2}{n}}\right)×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{1}+{n}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\pi}}×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}{n}}+\mathrm{1}\right)} \\ $$$${wait}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

Another approach... 1≥sinx≥0 1≥(sinx)^(1/n) ≥0 (2/π)×∫_0 ^(π/2) 1×dx≥(2/π)∫_0 ^(π/2) (sinx)^(1/n) dx≥(2/π)∫_0 ^(π/2) 0×dx 2≥(2/π)∫_0 ^(π/2) (sinx)^(1/n) dx≥0 2^n ≥[(2/π)∫_0 ^(π/2) (sinx)^(1/n) dx]^n ≥0

$${Another}\:{approach}... \\ $$$$\:\mathrm{1}\geqslant{sinx}\geqslant\mathrm{0} \\ $$$$\mathrm{1}\geqslant\left({sinx}\right)^{\frac{\mathrm{1}}{{n}}} \geqslant\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\pi}×\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}×{dx}\geqslant\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sinx}\right)^{\frac{\mathrm{1}}{{n}}} {dx}\geqslant\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{0}×{dx} \\ $$$$\mathrm{2}\geqslant\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sinx}\right)^{\frac{\mathrm{1}}{{n}}} {dx}\geqslant\mathrm{0} \\ $$$$\mathrm{2}^{{n}} \geqslant\left[\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left({sinx}\right)^{\frac{\mathrm{1}}{{n}}} {dx}\right]^{{n}} \geqslant\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com