Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 50460 by ajfour last updated on 16/Dec/18

Commented by ajfour last updated on 16/Dec/18

Find r in terms of R.

$${Find}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of}\:\boldsymbol{{R}}. \\ $$

Commented by MJS last updated on 18/Dec/18

I solved this for 2 small circles with r=1 and . a parabola y=ax^2 . a circle x^2 +(y−r)^2 =r^2 . an ellipse (x^2 /a^2 )+(((y−b)^2 )/b^2 )=1 [this one is tricky, will post soon] will also try for a hyperbola

$$\mathrm{I}\:\mathrm{solved}\:\mathrm{this}\:\mathrm{for}\:\mathrm{2}\:\mathrm{small}\:\mathrm{circles}\:\mathrm{with}\:{r}=\mathrm{1}\:\mathrm{and} \\ $$$$.\:\mathrm{a}\:\mathrm{parabola}\:{y}={ax}^{\mathrm{2}} \\ $$$$.\:\mathrm{a}\:\mathrm{circle}\:{x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$.\:\mathrm{an}\:\mathrm{ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\:\:\:\:\:\left[\mathrm{this}\:\mathrm{one}\:\mathrm{is}\:\mathrm{tricky},\:\mathrm{will}\:\mathrm{post}\:\mathrm{soon}\right] \\ $$$$\mathrm{will}\:\mathrm{also}\:\mathrm{try}\:\mathrm{for}\:\mathrm{a}\:\mathrm{hyperbola} \\ $$

Answered by mr W last updated on 16/Dec/18

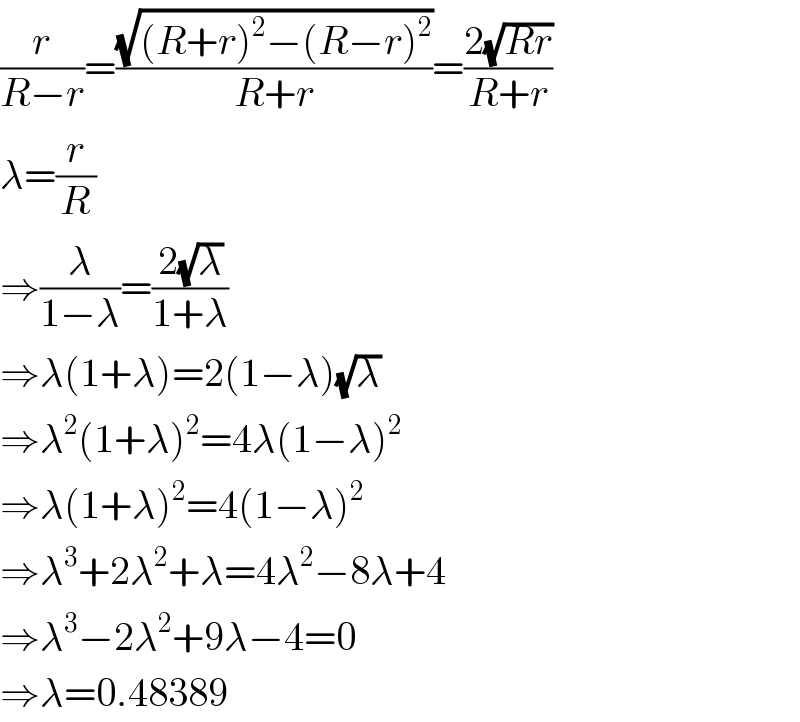
(r/(R−r))=((√((R+r)^2 −(R−r)^2 ))/(R+r))=((2(√(Rr)))/(R+r)) λ=(r/R) ⇒(λ/(1−λ))=((2(√λ))/(1+λ)) ⇒λ(1+λ)=2(1−λ)(√λ) ⇒λ^2 (1+λ)^2 =4λ(1−λ)^2 ⇒λ(1+λ)^2 =4(1−λ)^2 ⇒λ^3 +2λ^2 +λ=4λ^2 −8λ+4 ⇒λ^3 −2λ^2 +9λ−4=0 ⇒λ=0.48389

$$\frac{{r}}{{R}−{r}}=\frac{\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }}{{R}+{r}}=\frac{\mathrm{2}\sqrt{{Rr}}}{{R}+{r}} \\ $$$$\lambda=\frac{{r}}{{R}} \\ $$$$\Rightarrow\frac{\lambda}{\mathrm{1}−\lambda}=\frac{\mathrm{2}\sqrt{\lambda}}{\mathrm{1}+\lambda} \\ $$$$\Rightarrow\lambda\left(\mathrm{1}+\lambda\right)=\mathrm{2}\left(\mathrm{1}−\lambda\right)\sqrt{\lambda} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} \left(\mathrm{1}+\lambda\right)^{\mathrm{2}} =\mathrm{4}\lambda\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda^{\mathrm{3}} +\mathrm{2}\lambda^{\mathrm{2}} +\lambda=\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{8}\lambda+\mathrm{4} \\ $$$$\Rightarrow\lambda^{\mathrm{3}} −\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{9}\lambda−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{48389} \\ $$

Commented by ajfour last updated on 16/Dec/18

Thanks for solving Sir.

$${Thanks}\:{for}\:{solving}\:{Sir}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

sir pls explain thd first line pls...

$${sir}\:{pls}\:{explain}\:{thd}\:{first}\:{line}\:{pls}... \\ $$

Commented by mr W last updated on 17/Dec/18

Commented by mr W last updated on 17/Dec/18

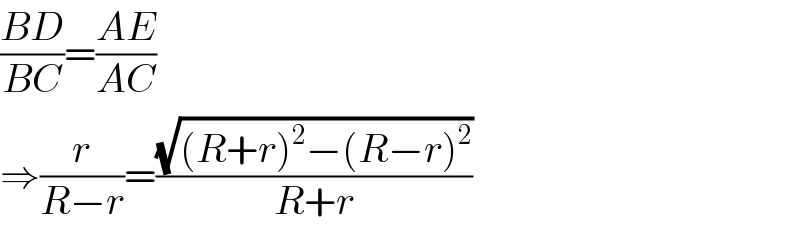
((BD)/(BC))=((AE)/(AC)) ⇒(r/(R−r))=((√((R+r)^2 −(R−r)^2 ))/(R+r))

$$\frac{{BD}}{{BC}}=\frac{{AE}}{{AC}} \\ $$$$\Rightarrow\frac{{r}}{{R}−{r}}=\frac{\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }}{{R}+{r}} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

excellent thank you sir...

$${excellent}\:{thank}\:{you}\:\:{sir}... \\ $$

Commented by ajfour last updated on 17/Dec/18

cos ∠DBC = cos θ =((DB)/(BC))= (r/(R−r)) sin ∠CAE = sin θ = ((CE)/(CA)) = ((R−r)/(R+r)) hence ((r/(R−r)))^2 + (((R−r)/(R+r)))^2 =1 let x=(r/R) ⇒ ((x/(1−x)))^2 + (((1−x)/(1+x)))^2 = 1 ⇒ x^2 (1+x)^2 + (1−x)^4 = (1−x^2 )^2 x^4 +2x^3 +x^2 +1+x^4 −4x+6x^2 −4x^3 = 1+x^4 −2x^2 ⇒ x^4 −2x^3 +9x^2 −4x = 0 if x≠0, x^3 −2x^2 +9x−4 = 0

$$\mathrm{cos}\:\angle{DBC}\:=\:\mathrm{cos}\:\theta\:=\frac{{DB}}{{BC}}=\:\frac{{r}}{{R}−{r}} \\ $$$$\mathrm{sin}\:\angle{CAE}\:=\:\mathrm{sin}\:\theta\:=\:\frac{{CE}}{{CA}}\:=\:\frac{{R}−{r}}{{R}+{r}} \\ $$$${hence}\:\:\:\:\left(\frac{{r}}{{R}−{r}}\right)^{\mathrm{2}} +\:\left(\frac{{R}−{r}}{{R}+{r}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${let}\:\:{x}=\frac{{r}}{{R}} \\ $$$$\Rightarrow\:\:\left(\frac{{x}}{\mathrm{1}−{x}}\right)^{\mathrm{2}} +\:\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\mathrm{2}} +\:\left(\mathrm{1}−{x}\right)^{\mathrm{4}} \:=\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \:+\mathrm{1}+{x}^{\mathrm{4}} −\mathrm{4}{x}+\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{x}\:=\:\mathrm{0} \\ $$$${if}\:\:{x}\neq\mathrm{0}, \\ $$$$\:\:\:\:\:\:\:{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}−\mathrm{4}\:=\:\mathrm{0} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

thank you sir...

$${thank}\:{you}\:{sir}... \\ $$

Answered by ajfour last updated on 16/Dec/18

i get r= 0.48389R

$${i}\:{get}\:{r}=\:\mathrm{0}.\mathrm{48389}{R} \\ $$

Commented by peter frank last updated on 16/Dec/18

please help QN 50349

$${please}\:\:{help}\:{QN}\:\mathrm{50349} \\ $$

Commented by ajfour last updated on 16/Dec/18

thanks Sir! for confirming.

$${thanks}\:{Sir}!\:{for}\:{confirming}. \\ $$

Commented by MJS last updated on 16/Dec/18

me too. I′ve been trying with an ellipse instead of the big circle, it seems very hard... not sure if it′s possible to solve.

$$\mathrm{me}\:\mathrm{too}. \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{trying}\:\mathrm{with}\:\mathrm{an}\:\mathrm{ellipse}\:\mathrm{instead}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{big}\:\mathrm{circle},\:\mathrm{it}\:\mathrm{seems}\:\mathrm{very}\:\mathrm{hard}...\:\mathrm{not}\:\mathrm{sure} \\ $$$$\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com