Question and Answers Forum
Question Number 50511 by behi83417@gmail.com last updated on 17/Dec/18
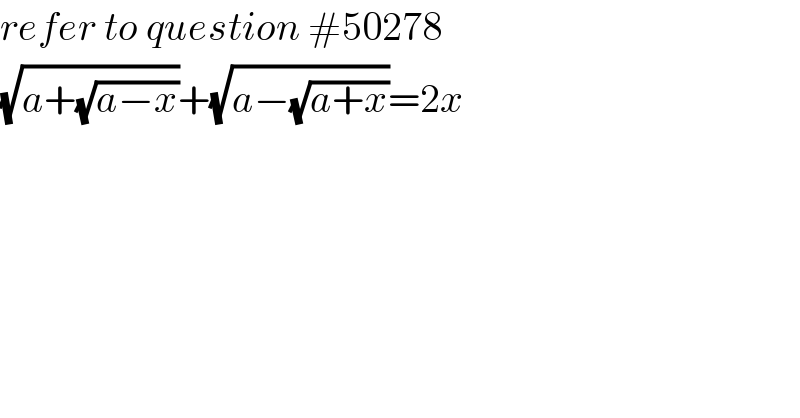
Answered by behi83417@gmail.com last updated on 17/Dec/18
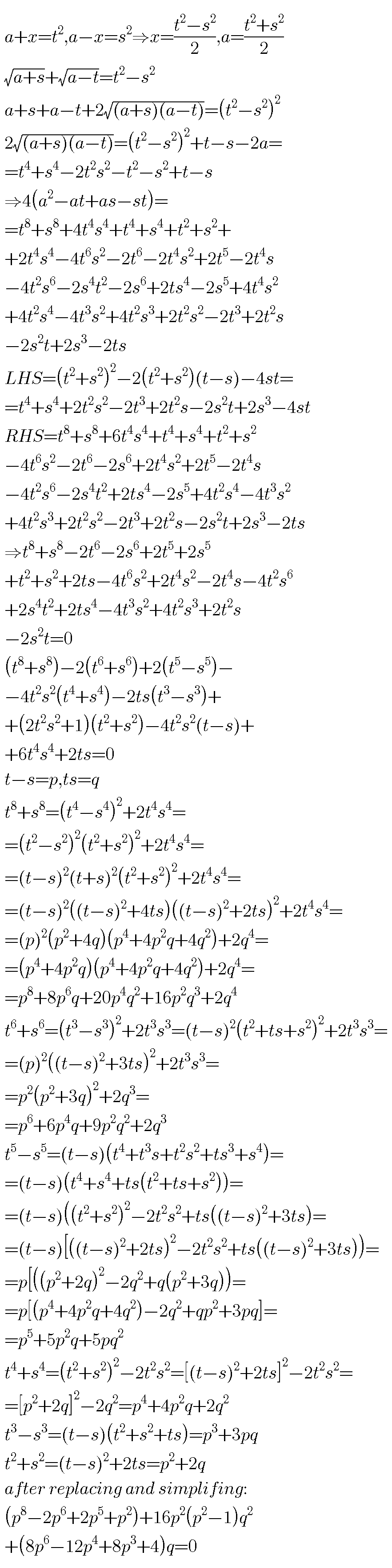
Commented by behi83417@gmail.com last updated on 17/Dec/18
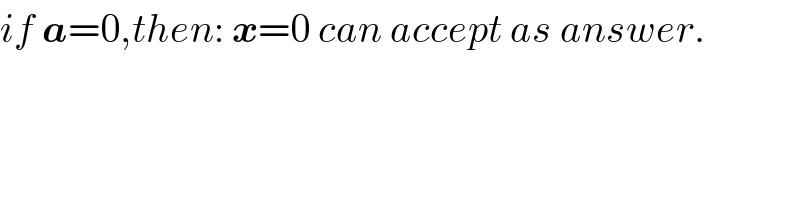
Commented by behi83417@gmail.com last updated on 17/Dec/18
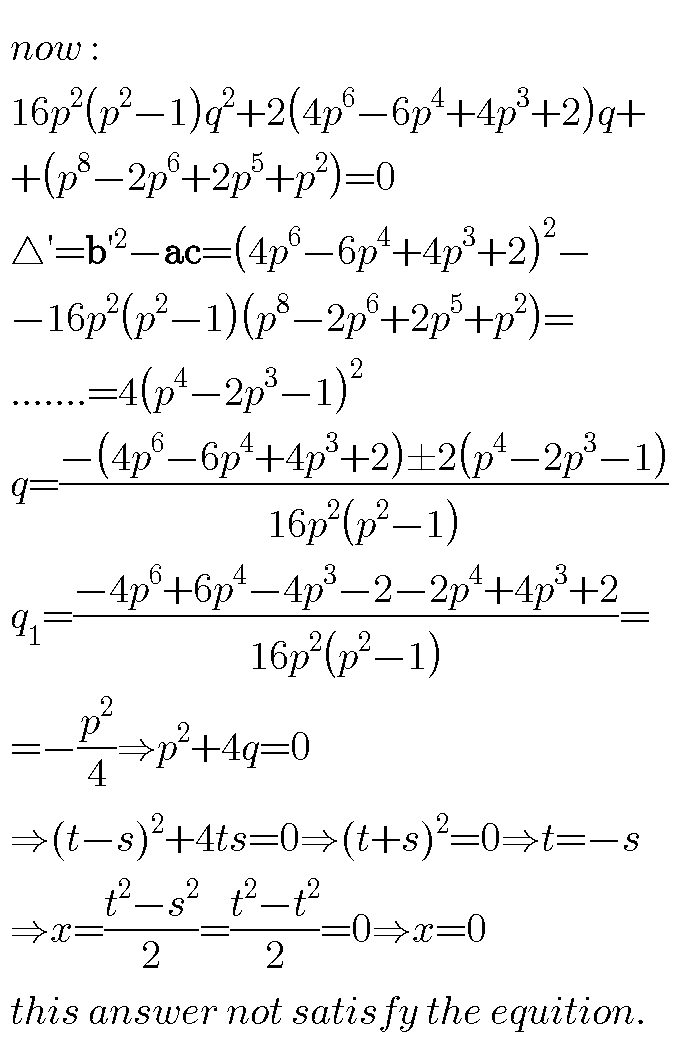
Commented by behi83417@gmail.com last updated on 17/Dec/18
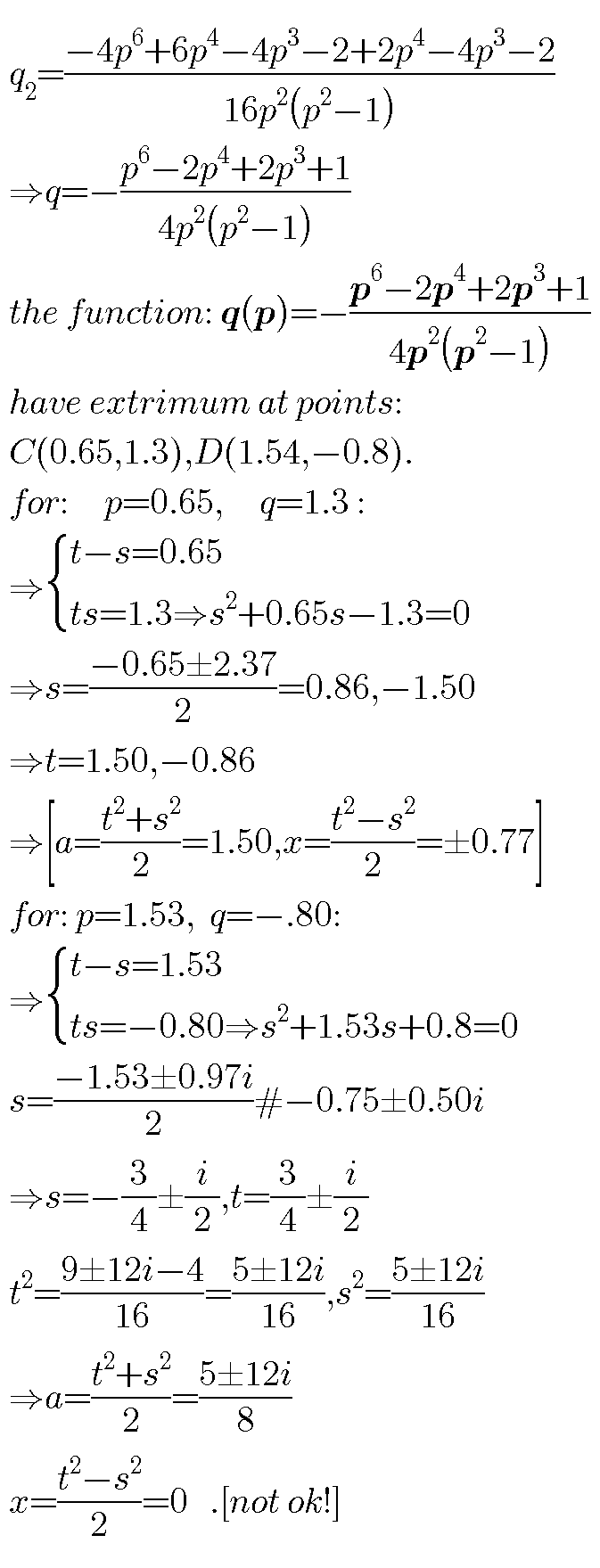
Commented by behi83417@gmail.com last updated on 17/Dec/18
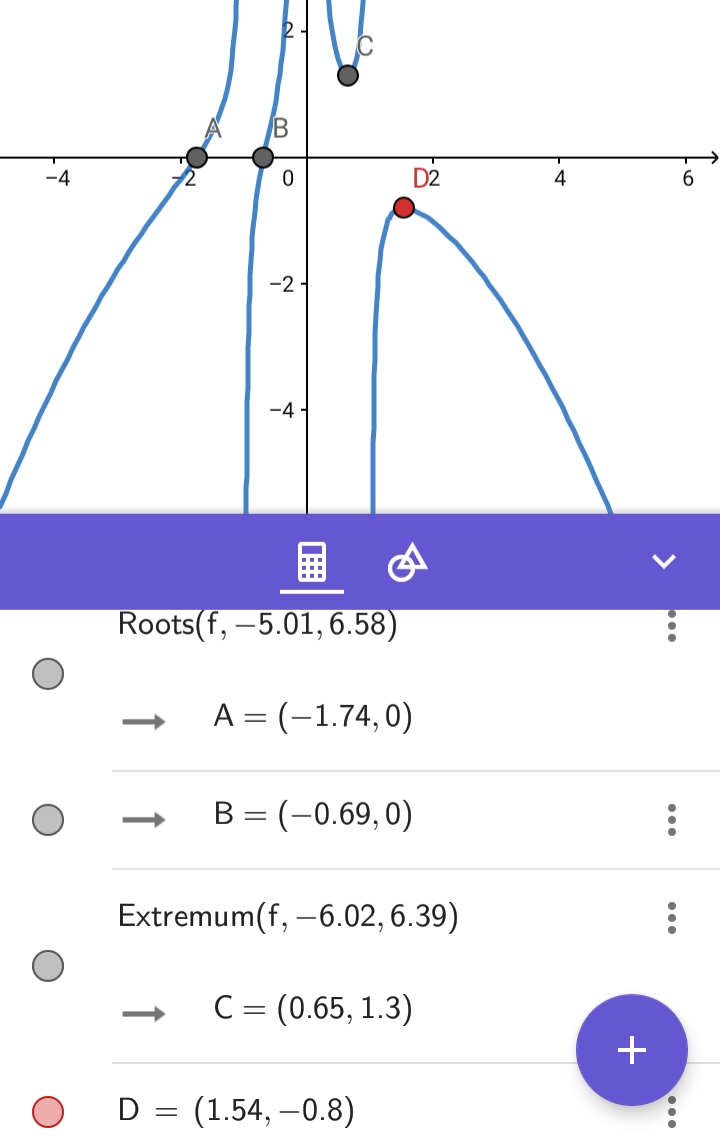
Commented by mr W last updated on 17/Dec/18
Commented by behi83417@gmail.com last updated on 17/Dec/18
![excuse me sir.i cant undrestand this commenet. [concrete=?]](Q50597.png)
Commented by mr W last updated on 17/Dec/18
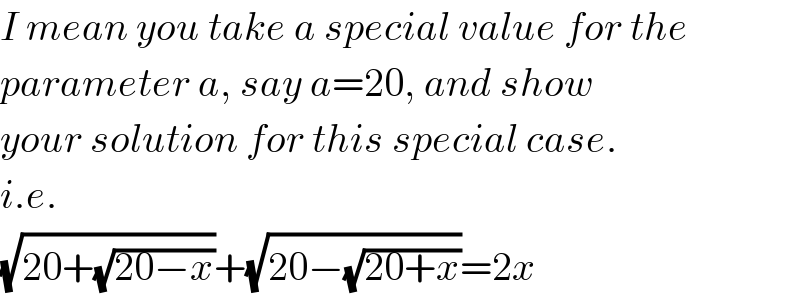
Commented by behi83417@gmail.com last updated on 18/Dec/18
![a=20,is too large and big numbers in solution.solve for:a=1 (√(1+(√(1−x))))+(√(1−(√(1+x))))=2x 1+x=t^2 ,1−x=s^2 ⇒x=((t^2 −s^2 )/2),t^2 +s^2 =2 (√(1+s))+(√(1−t))=t^2 −s^2 1+s+1−t+2(√((1+s)(1−t)))=(t^2 −s^2 )^2 4(1+s)(1−t)=[(t^2 −s^2 )^2 +t−s−2]^2 4−4t+4s−4ts=[t^4 +s^4 −2t^2 s^2 +t−s−2]^2 = =t^8 +s^8 +4t^4 s^4 +t^2 +s^2 +4+2t^4 s^4 −4t^6 s^2 +2t^5 −2t^4 s−4t^4 −4t^2 s^6 +2ts^4 −2s^5 −4s^4 −4t^3 s^2 +4t^2 s^3 +4t^2 s^2 −4t+4s−2ts (t^8 +s^8 )+2(t^5 −s^5 )+6t^4 s^4 +2ts+4t^2 s^2 −4t^2 s^2 (t^4 +s^4 )−2ts(t^3 −s^3 )+4(t^4 +s^4 ) −4t^2 s^2 (t−s)=0 (t^8 +s^8 )+2(t^5 −s^5 )−4(1+t^2 s^2 )(t^4 +s^4 ) −2ts(t^3 −s^3 )−4t^2 s^2 (t−s)+6t^4 s^4 + +8t^2 s^2 +2ts+(t^2 +s^2 )=0 let: t−s=p , ts=q t^8 +s^8 =p^8 +8p^6 q+20p^4 q^2 +16p^2 q^3 +2q^4 2(t^5 −s^5 )=2p^5 +10p^2 q+10pq^2 4(1−t^2 s^2 )(t^4 +s^4 )=4(p^4 +4p^2 q+2q^2 )(1−q^2 )= =4p^4 +16p^2 q+8q^2 −4p^4 q^2 −16p^2 q^3 −8q^4 −2ts(t^3 −s^3 )=−2q(p^3 +3pq)= =−2p^3 q−6pq^2 −4t^2 s^2 (t−s)=−4q^2 p −2p^3 q−10pq^2 +2q+4p^4 =0 16p^4 q^2 +2(4p^6 +4p^3 −8p^2 +2)q +(p^8 +2p^5 −4p^4 +p^2 )=0 △′=(4p^6 +4p^3 −8p^2 +2)^2 −16p^4 (p^8 +2p^5 −4p^4 +p^2 )= =4(2p^3 −4p^2 +1)^2 q=((−(4p^6 +4p^3 −8p^2 +2)±2(2p^3 −4p^2 +1))/(16p^4 ))= q_1 =((−4p^6 )/(16p^4 ))=−(p^2 /4) q_2 =−((p^6 +2p^3 −4p^2 +1)/(4p^4 )) for:q=−(p^2 /4)⇒p^2 +4q=0⇒(t−s)^2 +4ts=0 ⇒(t+s)^2 =0⇒t=−s⇒x=0 (not ok!) q(p)=−((p^6 +2p^3 −4p^2 +1)/(4p^4 )),have extrimums at points: E(−.64,1.63),F(.75,.18) p=−.64⇒t−s=−0.64⇒t=s−0.64 q=1.63⇒ts=1.63⇒s(s−.64)=1.63 ⇒s^2 −0.64s−1.63=0⇒s=((.64±2.63)/2) ⇒s=1.64,−1⇒t=1,−1.64 ⇒x=((t^2 −s^2 )/2)=((1.64^2 −1)/2)=±0.84 (√(1+(√(1−0.84))))+(√(1−(√(1+0.84))))= =1.18+0.06i≠2×0.84 (√(1+(√(1+.84))))+(√(1−(√(1−.84))))≠2(−.84) ⇒x=±0.84 not answer. p=0.75⇒t−s=0.75⇒t=s+0.75 ts=.18⇒s(s+.75)=.18 ⇒s^2 +.75s−.18=0⇒s=((−.75±1.13)/2) ⇒s=−.94,0.19 , t=−.19,0.94 x=(((.94)^2 −(.19)^2 )/2)=±0.42 (√(1+(√(1−.42))))+(√(1−(√(1+.42))))≠2×(.42) (√(1+(√(1+.42))))+(√(1−(√(1−.42))))≠2(−.42) ⇒x=±.42 not answer.](Q50612.png)
Commented by mr W last updated on 18/Dec/18

Commented by behi83417@gmail.com last updated on 18/Dec/18