
Question Number 5056 by Rasheed Soomro last updated on 06/Apr/16

$${x}\neq{y}\:\wedge\:{y}\neq\mathrm{0}\:\wedge\:\mathrm{log}_{\frac{\mathrm{x}}{\mathrm{y}}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{y}^{\mathrm{3}} }\right)=? \\ $$
Commented by Yozzii last updated on 06/Apr/16
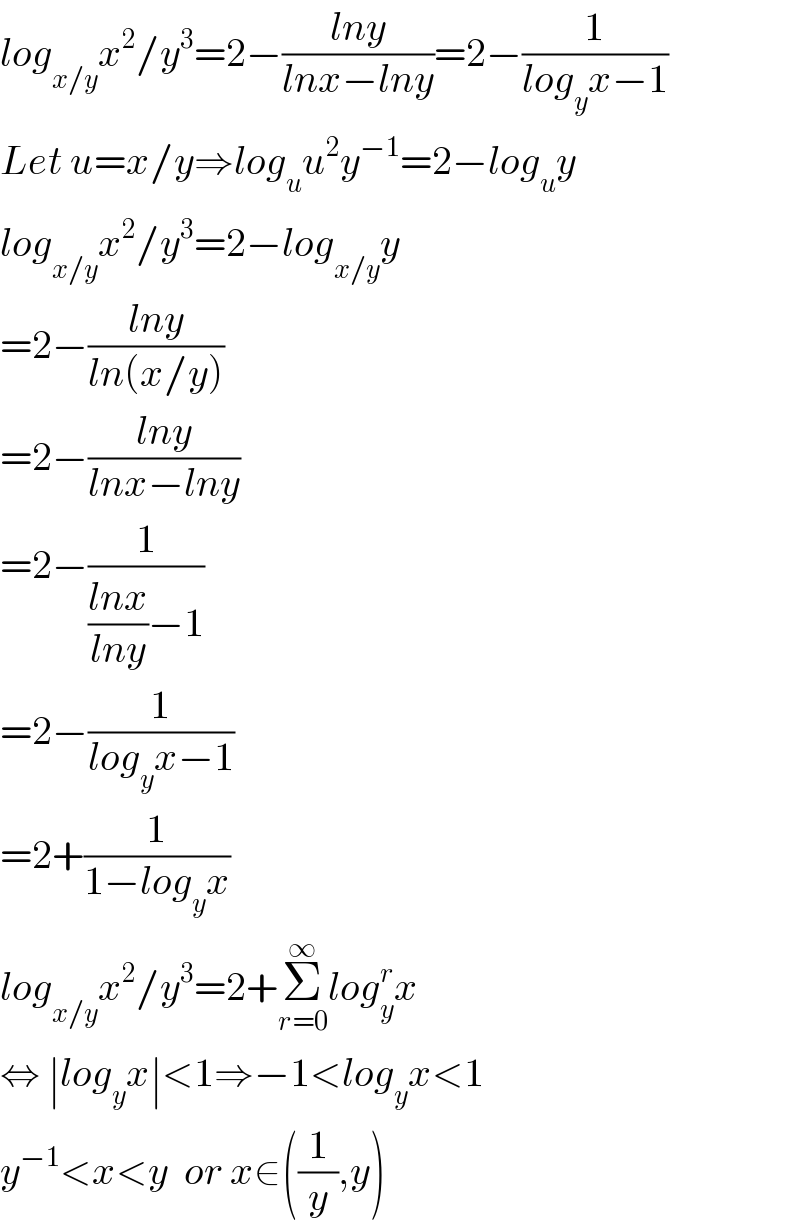
$${log}_{{x}/{y}} {x}^{\mathrm{2}} /{y}^{\mathrm{3}} =\mathrm{2}−\frac{{lny}}{{lnx}−{lny}}=\mathrm{2}−\frac{\mathrm{1}}{{log}_{{y}} {x}−\mathrm{1}} \\ $$$${Let}\:{u}={x}/{y}\Rightarrow{log}_{{u}} {u}^{\mathrm{2}} {y}^{−\mathrm{1}} =\mathrm{2}−{log}_{{u}} {y} \\ $$$${log}_{{x}/{y}} {x}^{\mathrm{2}} /{y}^{\mathrm{3}} =\mathrm{2}−{log}_{{x}/{y}} {y} \\ $$$$=\mathrm{2}−\frac{{lny}}{{ln}\left({x}/{y}\right)} \\ $$$$=\mathrm{2}−\frac{{lny}}{{lnx}−{lny}} \\ $$$$=\mathrm{2}−\frac{\mathrm{1}}{\frac{{lnx}}{{lny}}−\mathrm{1}} \\ $$$$=\mathrm{2}−\frac{\mathrm{1}}{{log}_{{y}} {x}−\mathrm{1}} \\ $$$$=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{1}−{log}_{{y}} {x}} \\ $$$${log}_{{x}/{y}} {x}^{\mathrm{2}} /{y}^{\mathrm{3}} =\mathrm{2}+\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{log}_{{y}} ^{{r}} {x} \\ $$$$\Leftrightarrow\:\mid{log}_{{y}} {x}\mid<\mathrm{1}\Rightarrow−\mathrm{1}<{log}_{{y}} {x}<\mathrm{1} \\ $$$${y}^{−\mathrm{1}} <{x}<{y}\:\:{or}\:{x}\in\left(\frac{\mathrm{1}}{{y}},{y}\right) \\ $$
Commented by Rasheed Soomro last updated on 07/Apr/16
![log_(x/y) x^2 /y^3 =2+Σ_(r=0) ^∞ log_y ^r x [ Didn′t understand,how?]](Q5069.png)
$${log}_{{x}/{y}} {x}^{\mathrm{2}} /{y}^{\mathrm{3}} =\mathrm{2}+\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{log}_{{y}} ^{{r}} {x}\:\left[\:{Didn}'{t}\:{understand},{how}?\right] \\ $$
Commented by Yozzii last updated on 07/Apr/16
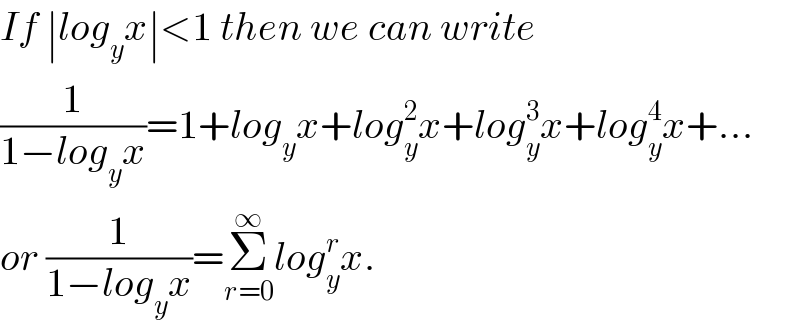
$${If}\:\mid{log}_{{y}} {x}\mid<\mathrm{1}\:{then}\:{we}\:{can}\:{write} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{log}_{{y}} {x}}=\mathrm{1}+{log}_{{y}} {x}+{log}_{{y}} ^{\mathrm{2}} {x}+{log}_{{y}} ^{\mathrm{3}} {x}+{log}_{{y}} ^{\mathrm{4}} {x}+... \\ $$$${or}\:\frac{\mathrm{1}}{\mathrm{1}−{log}_{{y}} {x}}=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{log}_{{y}} ^{{r}} {x}. \\ $$
Commented by Rasheed Soomro last updated on 07/Apr/16

$$\mathbb{T}\boldsymbol{\mathrm{h}\alpha\mathrm{n}}\Bbbk\boldsymbol{\mathrm{S}}! \\ $$
