
Question Number 5058 by Yozzii last updated on 06/Apr/16

$$\int\int\frac{{a}}{\left(\mathrm{1}−{lnx}\right)\left({lny}−\mathrm{1}\right)}{dxdy}=? \\ $$
Commented by Yozzii last updated on 06/Apr/16

$$\int\int\int\int...\int\int\int\frac{{a}}{\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{lnx}_{{i}} \right)}{dx}_{\mathrm{1}} {dx}_{\mathrm{2}} ...{dx}_{{n}} =? \\ $$
Commented by prakash jain last updated on 07/Apr/16
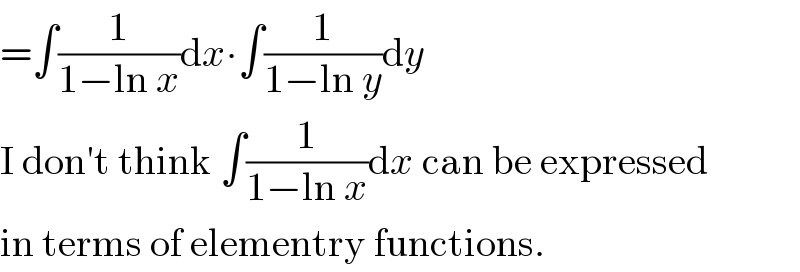
$$=\int\frac{\mathrm{1}}{\mathrm{1}−\mathrm{ln}\:{x}}\mathrm{d}{x}\centerdot\int\frac{\mathrm{1}}{\mathrm{1}−\mathrm{ln}\:{y}}\mathrm{d}{y} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\int\frac{\mathrm{1}}{\mathrm{1}−\mathrm{ln}\:{x}}\mathrm{d}{x}\:\mathrm{can}\:\mathrm{be}\:\mathrm{expressed} \\ $$$$\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{elementry}\:\mathrm{functions}. \\ $$
Commented by Yozzii last updated on 07/Apr/16

$${Wolfram}\:{alpha}\:{defines}\:{the}\:{En}\:{function} \\ $$$${for}\:{n}=\mathrm{1}\:{as}\:{E}_{\mathrm{1}} \left({x}\right)=\overset{\infty} {\int}_{\mathrm{1}} \frac{{e}^{−{tx}} }{{t}}{dt}=\int_{{x}} ^{\infty} \frac{{e}^{−{u}} }{{u}}{du}.\:{Now},\:{define}\:{the} \\ $$$${exponential}\:{integral}\:{Ei}\left({x}\right)\:{such}\:{that} \\ $$$${E}_{\mathrm{1}} \left({x}\right)=−{Ei}\left(−{x}\right).\:{Then} \\ $$$${Ei}\left({x}\right)=−\int_{−{x}} ^{\infty} \frac{{e}^{−{t}} }{{t}}{dt}. \\ $$$${Let}\:{u}=\mathrm{1}−{lnx}\Rightarrow{du}=−{x}^{−\mathrm{1}} {dx} \\ $$$${x}={e}^{\mathrm{1}−{u}} \Rightarrow−{e}^{\mathrm{1}−{u}} {du}={dx}. \\ $$$$\int\frac{{dx}}{\mathrm{1}−{lnx}}=\int\frac{−{e}^{\mathrm{1}−{u}} {du}}{{u}}=−{e}\int\frac{{e}^{−{u}} }{{u}}{du} \\ $$$$\int\frac{{dx}}{\mathrm{1}−{lnx}}={eEi}\left({u}\right)+{c}={eEi}\left(−\left(−{u}\right)\right)+{c}=−{eE}_{\mathrm{1}} \left(−{u}\right)+{c}=−{eE}_{\mathrm{1}} \left({lnx}−\mathrm{1}\right)+{c}. \\ $$$${I}'{m}\:{not}\:{certain}\:{whether}\:{or}\:{not}\: \\ $$$${I}'{m}\:{using}\:{this}\:{definition}\:{correctly}. \\ $$$$ \\ $$
