
Question and Answers Forum
Question Number 50659 by rahul 19 last updated on 18/Dec/18
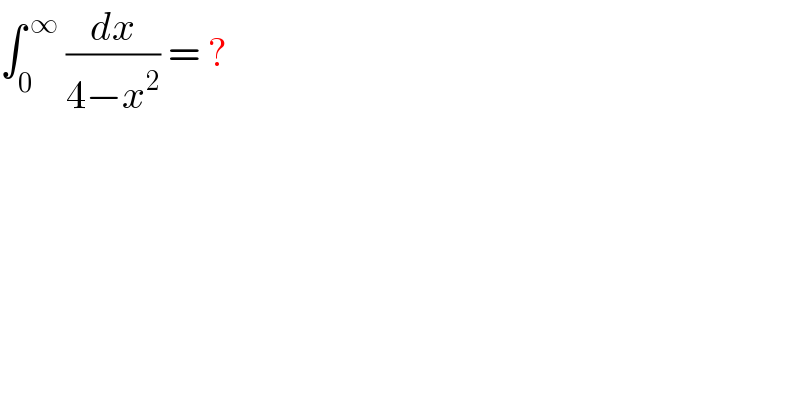
Commented by maxmathsup by imad last updated on 18/Dec/18
![this integral diverges let prove this let A_n =∫_0 ^(2+(1/n)) (dx/(4−x^2 )) we have ∫_0 ^2 (dx/(4−x^2 )) =lim_(n→+∞) A_n but A_n = (1/4) ∫_0 ^(2+(1/n)) ( (1/(2−x)) +(1/(2+x)))dx =(1/4)[ln∣((2+x)/(2−x))∣]_0 ^(2+(1/n)) = (1/4){ln∣ ((4+(1/n))/(−(1/n)))∣} =(1/4)ln(4n+1) ⇒lim_(n→+∞) A_n =+∞](Q50662.png)
Commented by mr W last updated on 18/Dec/18
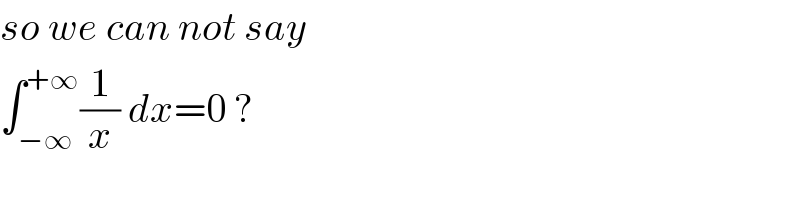
Commented by maxmathsup by imad last updated on 18/Dec/18
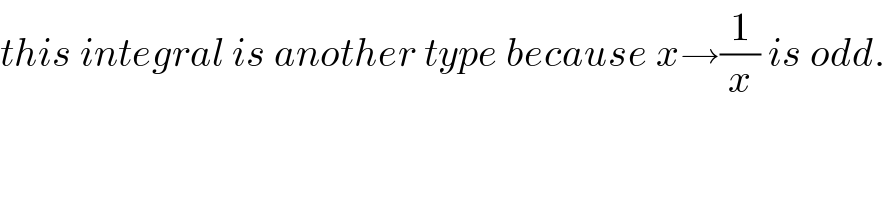
Commented by maxmathsup by imad last updated on 18/Dec/18
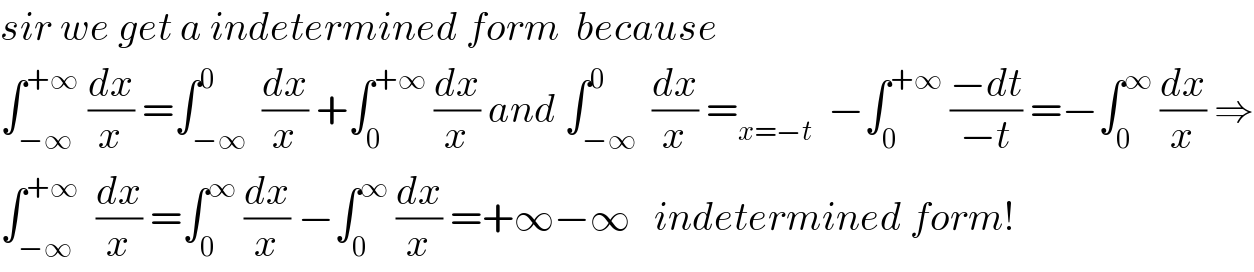
Answered by mr W last updated on 18/Dec/18
![∫_(0 ) ^( ∞) (dx/(2^2 −x^2 )) =(1/4)[ln ∣((2+x)/(2−x))∣]_0 ^2 +(1/4)[ln ∣((2+x)/(2−x))∣]_2 ^∞ =(1/4)(A)+(1/4)(−A) =0](Q50661.png)
Commented by rahul 19 last updated on 18/Dec/18
thanks sir!
Commented by mr W last updated on 18/Dec/18

Commented by afachri last updated on 18/Dec/18
Answered by MJS last updated on 18/Dec/18

