Question Number 50820 by ajfour last updated on 20/Dec/18
Commented by ajfour last updated on 20/Dec/18
$${Choose}\:{your}\:{origin}\:{and}\:{find}\: \\ $$$${equation}\:{of}\:{parabola}\:{such}\:{that} \\ $$$${it}\:{has}\:{maximum}\:{length}\:{inside} \\ $$$${ellipse}\:\left({parameters}\:{a}\:{and}\:{b}\right). \\ $$
Answered by ajfour last updated on 21/Dec/18
![y=Ax^2 −b bsin θ = Aa^2 cos^2 θ−b let sin θ = t ⇒ Aa^2 (1−t^2 )−b = bt other than t=−1 1−t = (b/(Aa^2 )) ⇒ t=1−(b/(Aa^2 )) ⇒ bsin θ = y_A = b−(b^2 /(Aa^2 )) x = (√((b+y)/A)) ⇒ (dx/dy) = (1/(2(√(A(b+y))))) L=∫_A ^( C) dl = 2∫_(−b) ^( y_A ) (√(1+((dx/dy))^2 )) dy = 2∫_(−b) ^( y_A ) (√(1+(1/(4A(b+y))))) dy (1/2)(dL/dA) = ∫_(−b) ^( y_A ) (((−(1/(4A^2 (b+y)))))/(2(√(1+(1/(4A(b+y))))))) dy +(b^2 /(A^2 a^2 ))(√(1+(1/(4A(2b−(b^2 /(Aa^2 ))))))) let I= ∫_(−b) ^( y_A ) ((1/((b+y)))/(√(1+(1/(4A(b+y)))))) dy =∫(dz/(√(z^2 +(z/(4A))))) = ∫(dz/(√((z+(1/(2A)))^2 −(1/(4A^2 ))))) = ln ∣z+c+(√((z+c)^2 −c^2 ))∣+k where [ c = (1/(2A)) ] y_A = b−(b^2 /(Aa^2 )) ; z_A =b+y_A =2b−((2b^2 c)/a^2 ) y_B = −b ⇒ z_B = 0 let z_A +c = t_A = 2b+(1/(2A))(1−((2b^2 )/a^2 )) t_B = z_B +c =(1/(2A)) I = ln ((t_A +(√(t_A ^2 −c^2 )))/t_B ) (dL/dA) = 0 ⇒ (I/(8A^2 )) = (b^2 /(A^2 a^2 ))(√(1+(1/(4A(2b−(b^2 /(Aa^2 ))))))) ⇒ ln ((t_A +(√(t_A ^2 −c^2 )))/t_B ) = ((8b^2 )/a^2 )(√(1+(1/(4At_A )))) ⇒ In here c = (1/(2A)) with t_A = 2b+(1/(2A))(1−((2b^2 )/a^2 )) ; t_B =(1/(2A)) A is obtainable from above equation. If for example A=0 ⇒ ln (1−((2b^2 )/a^2 )+(√((1−((2b^2 )/a^2 ))^2 −1))) = ((8b^2 )/a^2 )(√(1+2(1−((2b^2 )/a^2 )))) ⇒ b = 0 (naturally if within an ellipse with b→0 , parabola shall have maximum length if A=0 .](Q50822.png)
$${y}={Ax}^{\mathrm{2}} −{b} \\ $$$${b}\mathrm{sin}\:\theta\:=\:{Aa}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta−{b} \\ $$$${let}\:\:\mathrm{sin}\:\theta\:=\:{t} \\ $$$$\Rightarrow\:\:{Aa}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)−{b}\:=\:{bt} \\ $$$${other}\:{than}\:{t}=−\mathrm{1} \\ $$$$\:\:\:\:\mathrm{1}−{t}\:=\:\frac{{b}}{{Aa}^{\mathrm{2}} }\:\:\:\Rightarrow\:\:\:{t}=\mathrm{1}−\frac{{b}}{{Aa}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{b}\mathrm{sin}\:\theta\:=\:{y}_{{A}} \:=\:{b}−\frac{{b}^{\mathrm{2}} }{{Aa}^{\mathrm{2}} } \\ $$$$\:\:\:{x}\:=\:\sqrt{\frac{{b}+{y}}{{A}}}\:\:\:\Rightarrow\:\:\frac{{dx}}{{dy}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{A}\left({b}+{y}\right)}} \\ $$$$\:\:\:{L}=\int_{{A}} ^{\:\:{C}} {dl}\:=\:\mathrm{2}\int_{−{b}} ^{\:\:{y}_{{A}} } \sqrt{\mathrm{1}+\left(\frac{{dx}}{{dy}}\right)^{\mathrm{2}} }\:{dy} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\int_{−{b}} ^{\:\:{y}_{{A}} } \sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{A}\left({b}+{y}\right)}}\:{dy} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\frac{{dL}}{{dA}}\:=\:\int_{−{b}} ^{\:\:{y}_{{A}} } \frac{\left(−\frac{\mathrm{1}}{\mathrm{4}{A}^{\mathrm{2}} \left({b}+{y}\right)}\right)}{\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{A}\left({b}+{y}\right)}}}\:{dy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{b}^{\mathrm{2}} }{{A}^{\mathrm{2}} {a}^{\mathrm{2}} }\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{A}\left(\mathrm{2}{b}−\frac{{b}^{\mathrm{2}} }{{Aa}^{\mathrm{2}} }\right)}} \\ $$$$\:\:{let}\:{I}=\:\int_{−{b}} ^{\:\:{y}_{{A}} } \frac{\frac{\mathrm{1}}{\left({b}+{y}\right)}}{\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{A}\left({b}+{y}\right)}}}\:{dy} \\ $$$$\:\:\:\:\:\:=\int\frac{{dz}}{\sqrt{{z}^{\mathrm{2}} +\frac{{z}}{\mathrm{4}{A}}}}\:=\:\int\frac{{dz}}{\sqrt{\left({z}+\frac{\mathrm{1}}{\mathrm{2}{A}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{A}^{\mathrm{2}} }}} \\ $$$$=\:\:\mathrm{ln}\:\mid{z}+{c}+\sqrt{\left({z}+{c}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }\mid+{k} \\ $$$$\:\:\:\:\:\:\:\:{where}\:\left[\:\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{2}{A}}\:\:\:\right] \\ $$$${y}_{{A}} \:=\:{b}−\frac{{b}^{\mathrm{2}} }{{Aa}^{\mathrm{2}} }\:\:;\:\:{z}_{{A}} ={b}+{y}_{{A}} =\mathrm{2}{b}−\frac{\mathrm{2}{b}^{\mathrm{2}} {c}}{{a}^{\mathrm{2}} } \\ $$$${y}_{{B}} \:=\:−{b}\:\:\Rightarrow\:\:{z}_{{B}} \:=\:\mathrm{0} \\ $$$${let}\:\:{z}_{{A}} +{c}\:=\:{t}_{{A}} \:=\:\mathrm{2}{b}+\frac{\mathrm{1}}{\mathrm{2}{A}}\left(\mathrm{1}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:{t}_{{B}} \:=\:{z}_{{B}} +{c}\:=\frac{\mathrm{1}}{\mathrm{2}{A}} \\ $$$${I}\:=\:\mathrm{ln}\:\frac{{t}_{{A}} +\sqrt{{t}_{{A}} ^{\mathrm{2}} −{c}^{\mathrm{2}} }}{{t}_{{B}} } \\ $$$$\frac{{dL}}{{dA}}\:=\:\mathrm{0}\:\:\:\Rightarrow \\ $$$$\frac{{I}}{\mathrm{8}{A}^{\mathrm{2}} }\:=\:\frac{{b}^{\mathrm{2}} }{{A}^{\mathrm{2}} {a}^{\mathrm{2}} }\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{A}\left(\mathrm{2}{b}−\frac{{b}^{\mathrm{2}} }{{Aa}^{\mathrm{2}} }\right)}} \\ $$$$\:\:\:\: \\ $$$$\Rightarrow\:\mathrm{ln}\:\frac{{t}_{{A}} +\sqrt{{t}_{{A}} ^{\mathrm{2}} −{c}^{\mathrm{2}} }}{{t}_{{B}} }\:=\:\frac{\mathrm{8}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{At}_{{A}} }} \\ $$$$\Rightarrow\:{In}\:{here}\:\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{2}{A}} \\ $$$${with}\:{t}_{{A}} =\:\mathrm{2}{b}+\frac{\mathrm{1}}{\mathrm{2}{A}}\left(\mathrm{1}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\:\:;\:{t}_{{B}} =\frac{\mathrm{1}}{\mathrm{2}{A}} \\ $$$${A}\:{is}\:{obtainable}\:{from}\:{above}\:{equation}. \\ $$$${If}\:\:{for}\:{example}\:\:{A}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left(\mathrm{1}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\sqrt{\left(\mathrm{1}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{8}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\sqrt{\mathrm{1}+\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)} \\ $$$$\Rightarrow\:\:\:{b}\:=\:\mathrm{0}\:\:\:\left({naturally}\:{if}\:{within}\:{an}\right. \\ $$$${ellipse}\:{with}\:{b}\rightarrow\mathrm{0}\:,\:{parabola}\:{shall} \\ $$$${have}\:{maximum}\:{length}\:{if}\:{A}=\mathrm{0}\:. \\ $$
Commented by ajfour last updated on 21/Dec/18
$${mrW}\:{Sir}\:{can}\:{you}\:{cast}\:{a}\:{glance} \\ $$$${please}\:.. \\ $$
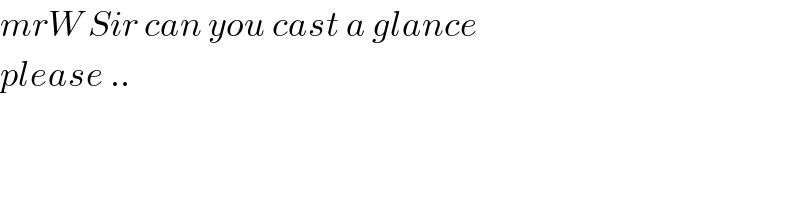
Commented by mr W last updated on 21/Dec/18
$${please}\:{check}\:{what}\:{is}\:{c}\:{in} \\ $$$$\Rightarrow\:\mathrm{ln}\:\frac{{t}_{{A}} +\sqrt{{t}_{{A}} ^{\mathrm{2}} −{c}^{\mathrm{2}} }}{{t}_{{B}} }\:=\:\frac{\mathrm{8}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{At}_{{A}} }} \\ $$$${in}\:{this}\:{eqn}.\:{we}\:{should}\:{only}\:{have}\:{a},{b},\:{A}. \\ $$
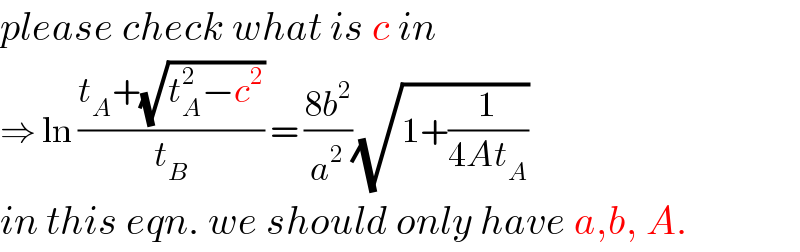
Commented by ajfour last updated on 21/Dec/18
$${Thank}\:{you}\:{Sir},\:\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{2}{A}}\:. \\ $$