Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 50849 by peter frank last updated on 21/Dec/18

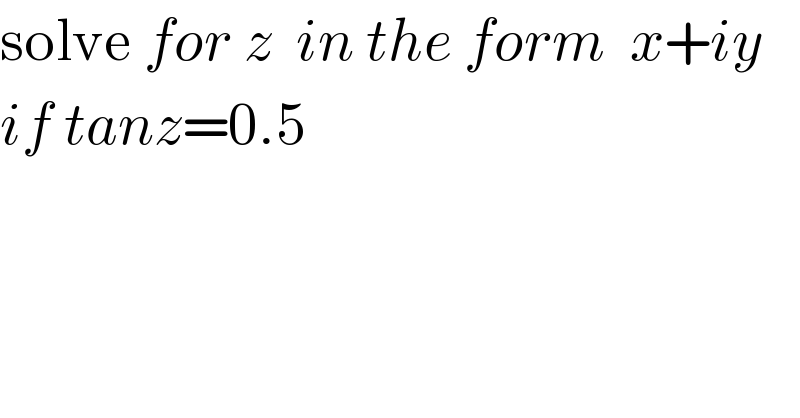
solve for z in the form x+iy if tanz=0.5

$$\mathrm{solve}\:{for}\:{z}\:\:{in}\:{the}\:{form}\:\:{x}+{iy}\: \\ $$$${if}\:{tanz}=\mathrm{0}.\mathrm{5}\: \\ $$

Answered by ajfour last updated on 21/Dec/18

e^(iz) = cos z+isin z e^(−iz) = cos z−isin z tan z= ((e^(iz) −e^(−iz) )/(i(e^(iz) +e^(−iz) ))) let e^(iz) = e^(−y+ix) = e^(−y) (cos x+isin x) ⇒ e^(−iz) = e^(y−ix) = e^y (cos x−isin x) ⇒ tan z = (((e^(−y) −e^y )cos x+i(e^(−y) +e^y )sin x)/(i[(e^(−y) +e^y )cos x+i(e^(−y) −e^y )sin x])) let e^(−y) +e^y = u , e^(−y) −e^y = v tan z = (((−ivcos x+usin x)(ucos x−ivsin x))/(u^2 cos^2 x+v^2 sin^2 x)) tan z = ((−iuv+(u^2 −v^2 )sin 2x)/(2(u^2 cos^2 x+v^2 sin^2 x))) if tan z = (1/2) , ⇒ uv = 0 or e^(−2y) =e^(2y) ⇒ y = 0 ⇒ u = 2 , v = 0 (((u^2 −v^2 )sin 2x)/(2(u^2 cos^2 x+v^2 sin^2 x))) = (1/2) ⇒ tan x = (1/2) ⇒ z = x = tan^(−1) (1/2)+nπ .

$${e}^{{iz}} \:=\:\mathrm{cos}\:{z}+{i}\mathrm{sin}\:{z} \\ $$$${e}^{−{iz}} \:=\:\mathrm{cos}\:{z}−{i}\mathrm{sin}\:{z} \\ $$$$\mathrm{tan}\:{z}=\:\frac{{e}^{{iz}} −{e}^{−{iz}} }{{i}\left({e}^{{iz}} +{e}^{−{iz}} \right)}\: \\ $$$${let}\:\:{e}^{{iz}} \:=\:{e}^{−{y}+{ix}} \:=\:{e}^{−{y}} \left(\mathrm{cos}\:{x}+{i}\mathrm{sin}\:{x}\right) \\ $$$$\Rightarrow\:\:\:{e}^{−{iz}} \:=\:{e}^{{y}−{ix}} =\:{e}^{{y}} \left(\mathrm{cos}\:{x}−{i}\mathrm{sin}\:{x}\right) \\ $$$$\Rightarrow\:\mathrm{tan}\:{z}\:=\:\frac{\left({e}^{−{y}} −{e}^{{y}} \right)\mathrm{cos}\:{x}+{i}\left({e}^{−{y}} +{e}^{{y}} \right)\mathrm{sin}\:{x}}{{i}\left[\left({e}^{−{y}} +{e}^{{y}} \right)\mathrm{cos}\:{x}+{i}\left({e}^{−{y}} −{e}^{{y}} \right)\mathrm{sin}\:{x}\right]} \\ $$$${let}\:\:{e}^{−{y}} +{e}^{{y}} \:=\:{u}\:\:,\:\:{e}^{−{y}} −{e}^{{y}} \:=\:{v} \\ $$$$\mathrm{tan}\:{z}\:=\:\frac{\left(−{iv}\mathrm{cos}\:{x}+{u}\mathrm{sin}\:{x}\right)\left({u}\mathrm{cos}\:{x}−{iv}\mathrm{sin}\:{x}\right)}{{u}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {x}+{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$$\:\mathrm{tan}\:{z}\:=\:\frac{−{iuv}+\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}\left({u}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {x}+{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}\right)} \\ $$$${if}\:\:\mathrm{tan}\:{z}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:,\:\Rightarrow \\ $$$$\:\:\:\:{uv}\:=\:\mathrm{0}\:\:\:{or}\:\:\:{e}^{−\mathrm{2}{y}} ={e}^{\mathrm{2}{y}} \:\:\: \\ $$$$\Rightarrow\:\:\:\:\:{y}\:=\:\mathrm{0}\:\:\:\: \\ $$$$\Rightarrow\:\:\:{u}\:=\:\mathrm{2}\:,\:\:{v}\:=\:\mathrm{0} \\ $$$$\:\frac{\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}\left({u}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {x}+{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\mathrm{tan}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\: \\ $$$$\Rightarrow\:\:\:\boldsymbol{{z}}\:=\:{x}\:=\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}+{n}\pi\:\:\:\:. \\ $$

Commented by peter frank last updated on 21/Dec/18

ans [ z=((πn)/2)+26.56+0.00000119i]

$${ans}\:\left[\:\:{z}=\frac{\pi\mathrm{n}}{\mathrm{2}}+\mathrm{26}.\mathrm{56}+\mathrm{0}.\mathrm{00000119}{i}\right] \\ $$

Commented by MJS last updated on 21/Dec/18

sorry but this is wrong. possibly the calculator approximates in a crazy way. tan (a+bi) =(1/2) has only real solutions ⇒ b=0

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{possibly}\:\mathrm{the}\:\mathrm{calculator} \\ $$$$\mathrm{approximates}\:\mathrm{in}\:\mathrm{a}\:\mathrm{crazy}\:\mathrm{way}. \\ $$$$\mathrm{tan}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{has}\:\mathrm{only}\:\mathrm{real}\:\mathrm{solutions}\:\Rightarrow\:{b}=\mathrm{0} \\ $$

Commented by peter frank last updated on 22/Dec/18

thank you both sirs

$${thank}\:{you}\:{both}\:{sirs} \\ $$

Answered by MJS last updated on 21/Dec/18

tan (x+iy) =(1/2); ((x),(y) )∈R^2 x+iy=nπ+arctan (1/2) ; n∈Z ⇒ y=0; x=nπ+arctan (1/2); n∈Z

$$\mathrm{tan}\:\left({x}+\mathrm{i}{y}\right)\:=\frac{\mathrm{1}}{\mathrm{2}};\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\in\mathbb{R}^{\mathrm{2}} \\ $$$${x}+\mathrm{i}{y}={n}\pi+\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{2}}\:;\:{n}\in\mathbb{Z} \\ $$$$\Rightarrow\:{y}=\mathrm{0};\:{x}={n}\pi+\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{2}};\:{n}\in\mathbb{Z} \\ $$

Answered by peter frank last updated on 21/Dec/18

tanh (iz)=itanz (1/2)=((tanh (iz))/i) (1/2)=((e^(iz) −e^(−iz) )/(i(e^(iz) +e^(−iz) ))) multiply by e^(iz) and simplify e^(2iz) =(3/5)+((4i)/5) z=x+iy e^(2ix) .e^(−2y) =(3/5)+((4i)/5) from Eurel′s form of complex no e^(2xi) =cos 2x+isin 2x e^(−2y) (cos 2x+isin 2x)=(3/4)+((4i)/5) compare real and Immarginary e^(−2y) cos 2x=(3/5)....(i) e^(−2y) sin 2x=(4/5)....(ii) divide ii by i tan2x=(4/3) tan2x=tan (53.13010235)≈tan 53.13 2x=πn+53.13^° x=((πn)/2)+26.565 n=0,1,2,3 .... from e^(−2y) cos 2x=(3/5)....(i) e^(−2y) =((0.6)/(cos 2x)) −2y=ln(((0.6)/(cos 2x))) y=(1/2)ln(((0.6)/(cos 2x))) z=x+iy z=((πn)/2)+26.565−(1/2)ln(((0.6)/(cos 2x))) ......

$$\:\mathrm{tanh}\:\left({iz}\right)={itanz} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{tanh}\:\left({iz}\right)}{{i}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\frac{{e}^{{iz}} −{e}^{−{iz}} }{{i}\left({e}^{{iz}} +{e}^{−{iz}} \right)} \\ $$$${multiply}\:{by}\:{e}^{{iz}} \:{and}\:{simplify} \\ $$$${e}^{\mathrm{2}{iz}} =\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{4}{i}}{\mathrm{5}} \\ $$$${z}={x}+{iy} \\ $$$${e}^{\mathrm{2}{ix}} .{e}^{−\mathrm{2}{y}} =\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{4}{i}}{\mathrm{5}} \\ $$$${from}\:{Eurel}'{s}\:{form}\:{of}\: \\ $$$${complex}\:{no} \\ $$$${e}^{\mathrm{2}{xi}} =\mathrm{cos}\:\mathrm{2}{x}+{i}\mathrm{sin}\:\mathrm{2}{x} \\ $$$${e}^{−\mathrm{2}{y}} \left(\mathrm{cos}\:\mathrm{2}{x}+{i}\mathrm{sin}\:\mathrm{2}{x}\right)=\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{4}{i}}{\mathrm{5}} \\ $$$${compare}\:{real}\:{and}\:{Immarginary} \\ $$$${e}^{−\mathrm{2}{y}} \mathrm{cos}\:\mathrm{2}{x}=\frac{\mathrm{3}}{\mathrm{5}}....\left({i}\right) \\ $$$${e}^{−\mathrm{2}{y}} \mathrm{sin}\:\:\mathrm{2}{x}=\frac{\mathrm{4}}{\mathrm{5}}....\left({ii}\right) \\ $$$${divide}\:{ii}\:{by}\:{i} \\ $$$${tan}\mathrm{2}{x}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${tan}\mathrm{2}{x}=\mathrm{tan}\:\left(\mathrm{53}.\mathrm{13010235}\right)\approx\mathrm{tan}\:\mathrm{53}.\mathrm{13} \\ $$$$\mathrm{2}{x}=\pi{n}+\mathrm{53}.\mathrm{13}^{°} \\ $$$${x}=\frac{\pi{n}}{\mathrm{2}}+\mathrm{26}.\mathrm{565} \\ $$$${n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$.... \\ $$$${from} \\ $$$${e}^{−\mathrm{2}{y}} \mathrm{cos}\:\mathrm{2}{x}=\frac{\mathrm{3}}{\mathrm{5}}....\left({i}\right) \\ $$$${e}^{−\mathrm{2}{y}} =\frac{\mathrm{0}.\mathrm{6}}{\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$−\mathrm{2}{y}={ln}\left(\frac{\mathrm{0}.\mathrm{6}}{\mathrm{cos}\:\mathrm{2}{x}}\right) \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{0}.\mathrm{6}}{\mathrm{cos}\:\mathrm{2}{x}}\right) \\ $$$${z}={x}+{iy} \\ $$$${z}=\frac{\pi{n}}{\mathrm{2}}+\mathrm{26}.\mathrm{565}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{0}.\mathrm{6}}{\mathrm{cos}\:\mathrm{2}{x}}\right) \\ $$$$...... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com