
Question and Answers Forum
Question Number 50892 by peter frank last updated on 21/Dec/18
![solve the equation tan 3θcotθ+1=0 for 0≤θ≤180 b)show that if cos 2θ is not zero then cos 2θ+sec 2θ=2[((cos^4 θ+sin^4 θ)/(cos^4 θ−sin^4 θ))] c)find the limit of ((tan (θ/3))/(3θ)) as θ→0](Q50892.png)
Answered by kaivan.ahmadi last updated on 21/Dec/18
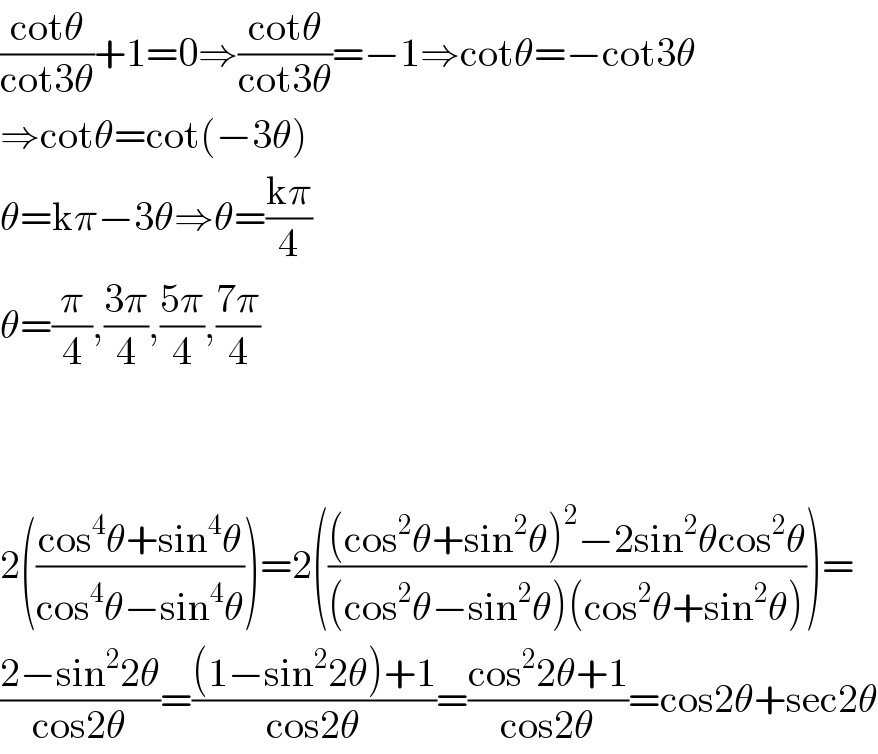
Answered by peter frank last updated on 21/Dec/18
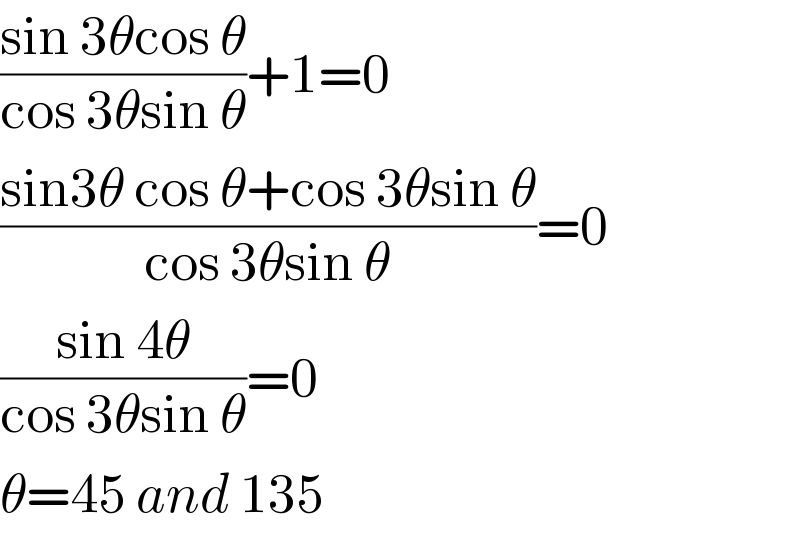
Answered by peter frank last updated on 21/Dec/18
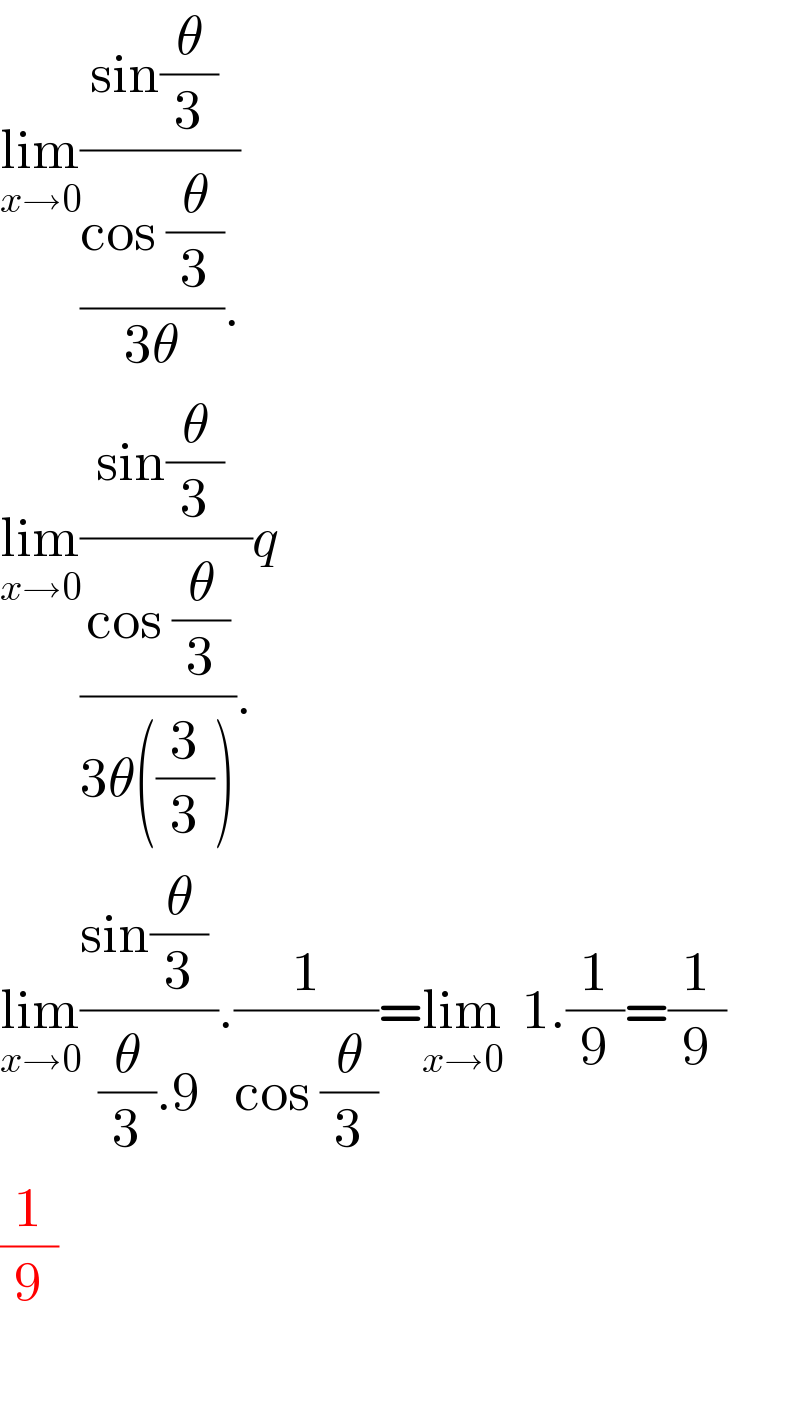
| ||
Question and Answers Forum | ||
Question Number 50892 by peter frank last updated on 21/Dec/18 | ||
![solve the equation tan 3θcotθ+1=0 for 0≤θ≤180 b)show that if cos 2θ is not zero then cos 2θ+sec 2θ=2[((cos^4 θ+sin^4 θ)/(cos^4 θ−sin^4 θ))] c)find the limit of ((tan (θ/3))/(3θ)) as θ→0](Q50892.png) | ||
Answered by kaivan.ahmadi last updated on 21/Dec/18 | ||
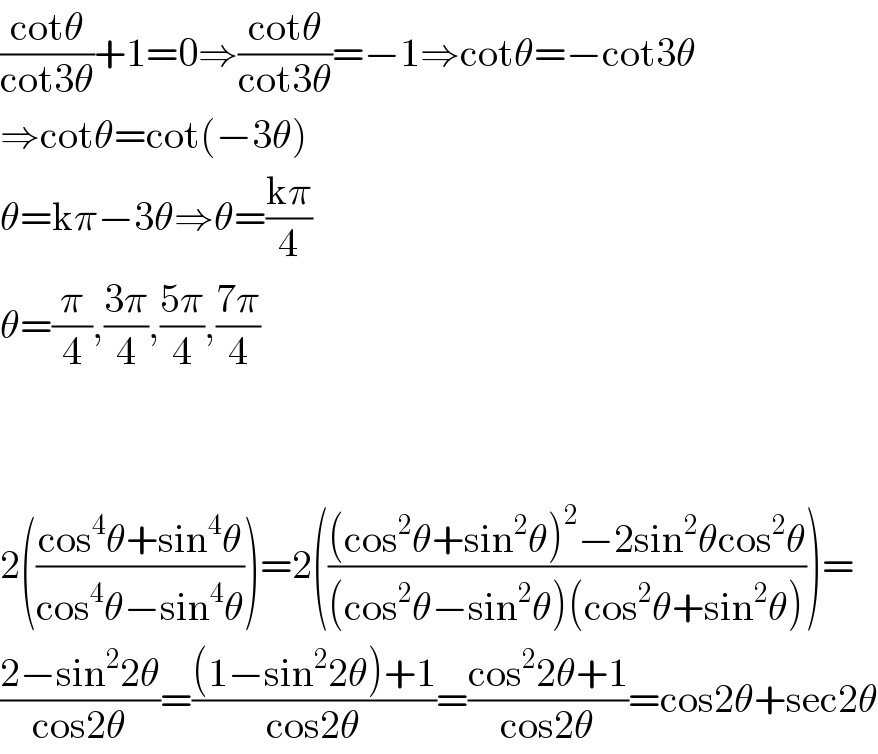 | ||
| ||
Answered by peter frank last updated on 21/Dec/18 | ||
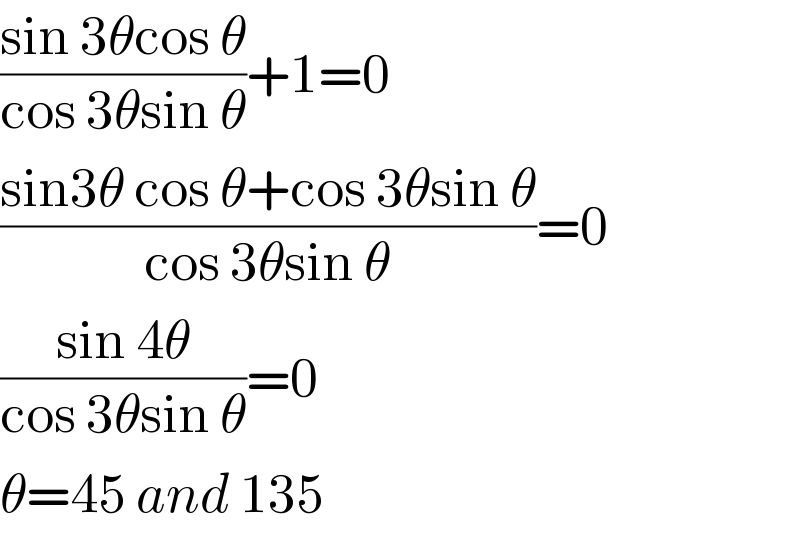 | ||
| ||
Answered by peter frank last updated on 21/Dec/18 | ||
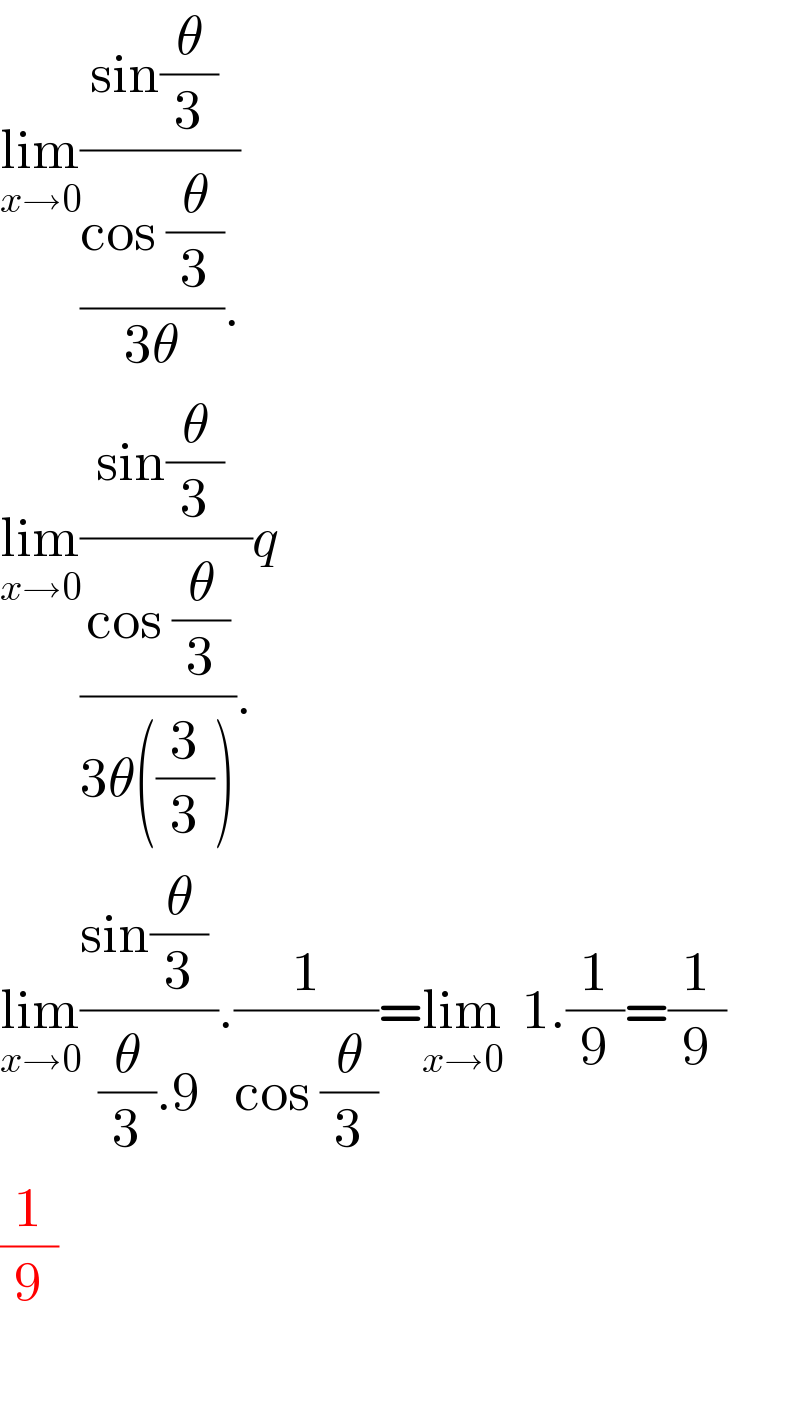 | ||
| ||