Question and Answers Forum
Question Number 50898 by ajfour last updated on 21/Dec/18

Commented by ajfour last updated on 21/Dec/18

Answered by ajfour last updated on 21/Dec/18
Commented by mr W last updated on 22/Dec/18
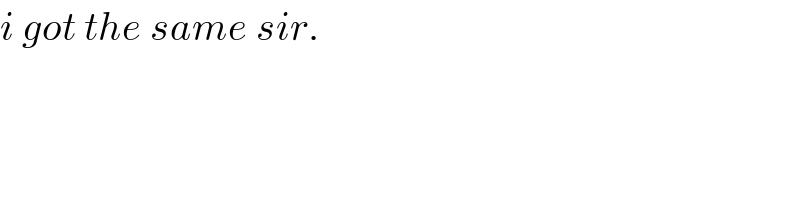
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Dec/18
![area sky=(1/2)×acosθ×bsinθ+∫_(bsinθ) ^b (a/b)(√(b^2 −y^2 )) dy =(a/b)[∣(y/2)(√(b^2 −y^2 )) +(b^2 /2)sin^(−1) ((y/b))∣_(bsinθ) ^b ]+(1/4)sin2θ =(a/b)[((b^2 /2)×(π/2))−(((bsinθ×bcosθ)/2)+(b^2 /2)θ)]+((sin2θ)/4) =((πab)/4)−((absin2θ)/4)+((abθ)/2)+((sin2θ)/4) given A_s =A_p =((πab)/8) at θ=θ_0 ((πab)/8)=((πab)/4)−((absin2θ_0 )/4)+((abθ_0 )/2)+((sin2θ_0 )/4) sin2θ_0 ×(1/4)(ab−1)−((ab)/2)sin^(−1) ((b^2 /(a^2 −b^2 )))=((πab)/8) length BP=(√((acosθ−0)^2 +(bsinθ+b)^2 )) =s s_(max) =l given s^2 =a^2 cos^2 θ+b^2 (1+sinθ)^2 2s×(ds/dθ)=a^2 ×−sin2θ+b^2 ×2(1+sinθ)(cosθ) 2b^2 cosθ+b^2 sin2θ−a^2 sin2θ=0 cosθ[2b^2 +2b^2 sinθ−2a^2 sinθ]=0 cosθ=0 θ=(π/2)←ignored sinθ_0 =(b^2 /(a^2 −b^2 )) cosθ_0 =((√((a^2 −b^2 )^2 −b^4 ))/((a^2 −b^2 )))=((√(a^4 −2a^2 b^2 ))/((a^2 −b^2 ))) wait...](Q50916.png)
Answered by mr W last updated on 22/Dec/18

Commented by OTCHRRE ABDULLAI last updated on 22/Dec/18

Commented by mr W last updated on 22/Dec/18
![r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ)) A_(red) =A_(blue) =((πab)/8) A_(red) =∫_0 ^θ ((r^2 dθ)/2)=((a^2 b^2 )/2)∫_0 ^θ (dθ/(a^2 sin^2 θ+b^2 cos^2 θ)) =((a^2 b^2 )/2)×((tan^(−1) ((a/b)tan θ))/(ab)) =((ab)/2)×tan^(−1) ((a/b)tan θ)=((πab)/8) ⇒tan^(−1) ((a/b)tan θ)=(π/4) ⇒(a/b)tan θ=1 ⇒tan θ=(b/a) ⇒ sin θ=(b/(√(a^2 +b^2 ))) and cos θ=(a/(√(a^2 +b^2 ))) P(r,θ) r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ))=((a^2 b^2 )/((2a^2 b^2 )/(a^2 +b^2 )))=((a^2 +b^2 )/2) (x/a^2 )+(y/b^2 )y′=0 ((r cos θ)/a^2 )+((r sin θ)/b^2 )y′=0 ⇒y′(at P)=−(b^2 /(a^2 tan θ))=−(b/a)=−tan α=−tan θ ⇒α=θ ϕ=(π/2)−α=(π/2)−θ r cos θ=l cos ϕ=l sin θ ⇒r=l tan θ=((lb)/a) r sin θ=l sin ϕ−b=l cos θ−b ⇒r=(l/(tan θ))−(b/(sin θ)) ⇒(l/(tan θ))−(b/(sin θ))=l tan θ ⇒b=l((1/(tan θ))−tan θ)sin θ=l×((a^2 −b^2 )/(ab))×(b/(√(a^2 +b^2 ))) ⇒l=((ab(√(a^2 +b^2 )))/(a^2 −b^2 )) r^2 =((l^2 b^2 )/a^2 )=(b^2 /a^2 )×((a^2 b^2 (a^2 +b^2 ))/((a^2 −b^2 )^2 ))=((b^4 (a^2 +b^2 ))/((a^2 −b^2 )^2 ))=((a^2 +b^2 )/2) ⇒(b^4 /((a^2 −b^2 )^2 ))=(1/2) ((√2)b^2 )^2 −(a^2 −b^2 )^2 =0 [((√2)+1)b^2 −a^2 ][((√2)−1)b^2 +a^2 ]=0 ⇒a^2 =((√2)+1)b^2 ⇒l=((ab(√(a^2 +b^2 )))/(a^2 −b^2 ))=((ab(√((2+(√2))b^2 )))/((√2)b^2 ))=a(√((2+(√2))/2)) ⇒a=(√(2/(2+(√2)))) l=(√(2−(√2))) l ⇒b=(a/(√((√2)+1)))=(√((2−(√2))/((√2)+1))) l=(√(3(√2)−4)) l](Q50945.png)
Commented by ajfour last updated on 22/Dec/18

Commented by mr W last updated on 22/Dec/18

Commented by mr W last updated on 22/Dec/18
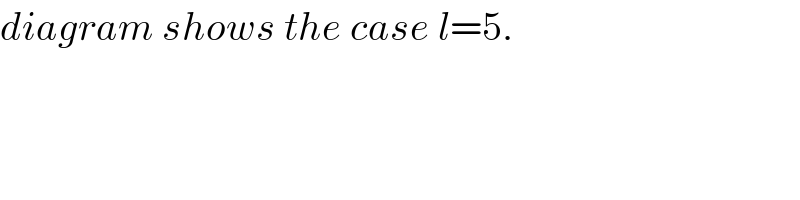
Commented by ajfour last updated on 22/Dec/18
Commented by OTCHRRE ABDULLAI last updated on 23/Dec/18

Commented by peter frank last updated on 22/Dec/18