
Question and Answers Forum
Question Number 51005 by Tawa1 last updated on 23/Dec/18

Commented by maxmathsup by imad last updated on 23/Dec/18

Commented by maxmathsup by imad last updated on 23/Dec/18
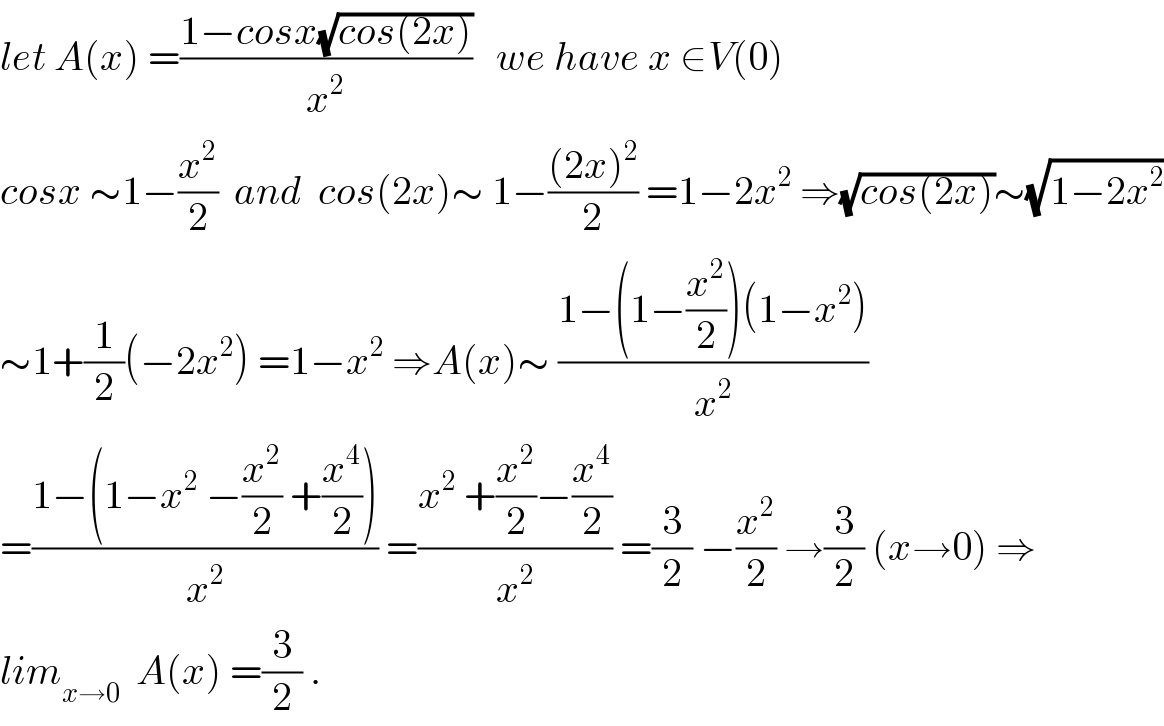
Commented by Tawa1 last updated on 24/Dec/18
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18
![2)t=θ−(π/6) lim_(t→0) ((sin(t))/((√3) −2cos(t+(π/6)))) =lim_(t→0) ((sint)/((√3) −2(cost.((√3)/2)−sint.(1/2)))) =lim_(t→0) ((sint)/((√3) −(√3) cost+sint)) =lim_(t→0) ((2sin(t/2)cos(t/2))/((√3) ×2sin^2 (t/2)+2sin(t/2)cos(t/2))) =lim_(t→0) ((cos(t/2))/((√3) sin(t/2)+cos(t/2)))=1 or method lim_(θ→((π )/6)) ((sin(θ−(π/6)))/(2[((√3)/2)−cos(θ)])) [((√3)/2)=cos(π/6)] (1/2)lim_(θ→((π )/6)) ((2sin(((θ−(π/6))/2))cos(((θ−(π/6))/2)))/(2sin((((π/6)+θ)/2))sin(((θ−(π/6))/2)))) =(1/2)×(1/(1/2))=1](Q51018.png)
Commented by Tawa1 last updated on 23/Dec/18
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18
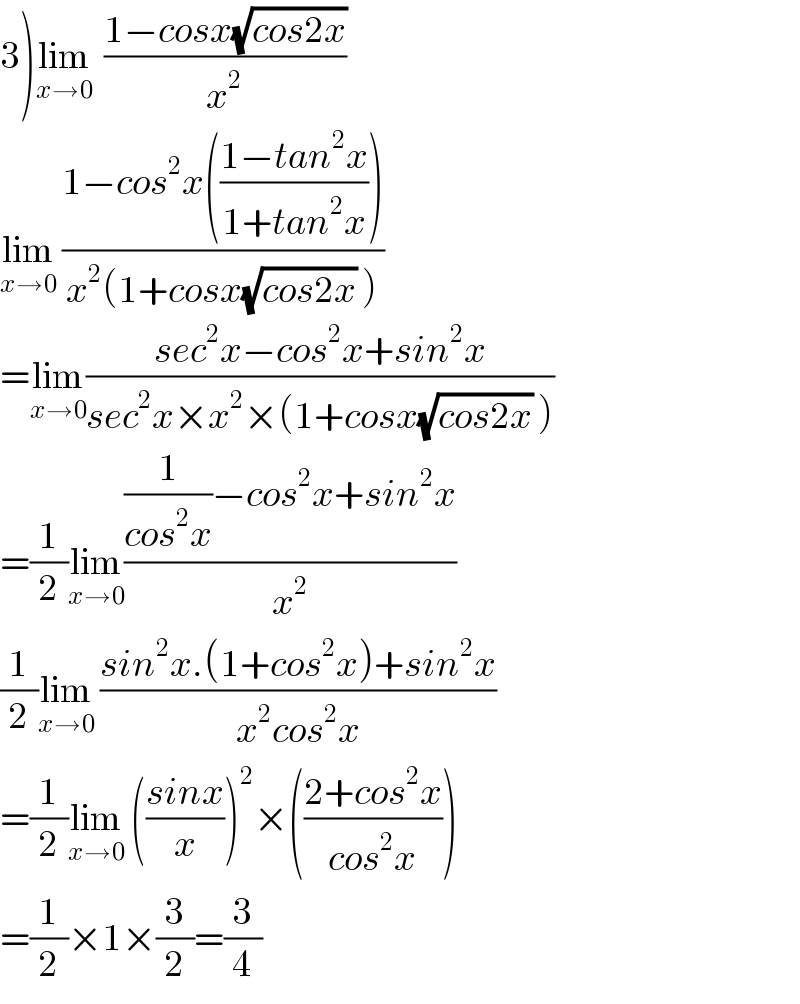
Commented by Tawa1 last updated on 23/Dec/18
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18
![1)lim_(y→0) ((x{sec(x+y)−secx}+ysec(x+y))/y) =x[lim_(y→0) ((sec(x+y)−secx)/y)]+secx =x[lim_(y→0) ((cosx−cos(x+y))/(ycosxcos(x+y)))]+secx =x[lim_(y→0) ((2sin(x+(y/2))sin((y/2)))/(cosxcos(x+y)×(y/2)×2))]+secx =x×((sinx)/(cos^2 x))+secx =xtanxsecx+secx](Q51022.png)
Commented by Tawa1 last updated on 23/Dec/18
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

