Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 51320 by Tawa1 last updated on 25/Dec/18

The points A, B, C represent the complex numbers z_1 , z_2 , z_3 respectively. And G is the centroid of the triangle A B C, if 4z_1 + z_2 + z_3 = 0, show that the origin is the mid point of AG.

$$\mathrm{The}\:\mathrm{points}\:\mathrm{A},\:\mathrm{B},\:\mathrm{C}\:\:\mathrm{represent}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{numbers}\:\:\mathrm{z}_{\mathrm{1}} ,\:\mathrm{z}_{\mathrm{2}} ,\:\mathrm{z}_{\mathrm{3}} \: \\ $$$$\mathrm{respectively}.\:\mathrm{And}\:\mathrm{G}\:\mathrm{is}\:\mathrm{the}\:\mathrm{centroid}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{A}\:\mathrm{B}\:\mathrm{C},\:\:\mathrm{if} \\ $$$$\mathrm{4z}_{\mathrm{1}} \:+\:\mathrm{z}_{\mathrm{2}} \:+\:\mathrm{z}_{\mathrm{3}} \:\:=\:\:\mathrm{0},\:\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mid}\:\mathrm{point}\:\mathrm{of}\:\:\mathrm{AG}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

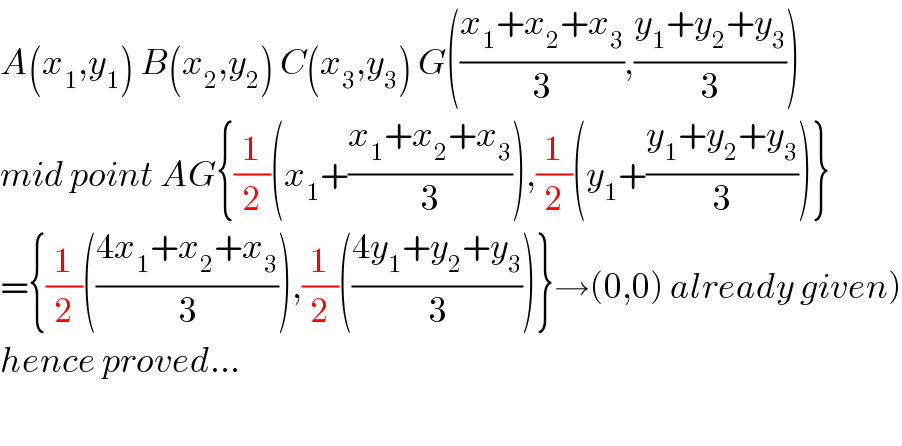
A(x_1 ,y_1 ) B(x_2 ,y_2 ) C(x_3 ,y_3 ) G(((x_1 +x_2 +x_3 )/3),((y_1 +y_2 +y_3 )/3)) mid point AG{(1/2)(x_1 +((x_1 +x_2 +x_3 )/3)),(1/2)(y_1 +((y_1 +y_2 +y_3 )/3))} ={(1/2)(((4x_1 +x_2 +x_3 )/3)),(1/2)(((4y_1 +y_2 +y_3 )/3))}→(0,0) already given) hence proved...

$${A}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:{B}\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)\:{C}\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} \right)\:{G}\left(\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} }{\mathrm{3}},\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +{y}_{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$${mid}\:{point}\:{AG}\left\{\frac{\mathrm{1}}{\mathrm{2}}\left({x}_{\mathrm{1}} +\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} }{\mathrm{3}}\right),\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{\mathrm{1}} +\frac{{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +{y}_{\mathrm{3}} }{\mathrm{3}}\right)\right\} \\ $$$$\left.=\left\{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} }{\mathrm{3}}\right),\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +{y}_{\mathrm{3}} }{\mathrm{3}}\right)\right\}\rightarrow\left(\mathrm{0},\mathrm{0}\right)\:{already}\:{given}\right) \\ $$$${hence}\:{proved}... \\ $$$$ \\ $$

Commented by Tawa1 last updated on 26/Dec/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 26/Dec/18

Sir but why is midpoint of AG not divided by 2, like (((x_1 + ((x_1 + x_2 + x_3 )/3))/2), .. i thought midpoint is divided by 2 sir. please let me understand sir

$$\mathrm{Sir}\:\mathrm{but}\:\mathrm{why}\:\mathrm{is}\:\mathrm{midpoint}\:\mathrm{of}\:\:\mathrm{AG}\:\:\mathrm{not}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{2},\:\:\mathrm{like} \\ $$$$\left(\frac{\mathrm{x}_{\mathrm{1}} \:+\:\frac{\mathrm{x}_{\mathrm{1}} \:+\:\mathrm{x}_{\mathrm{2}} \:+\:\mathrm{x}_{\mathrm{3}} }{\mathrm{3}}}{\mathrm{2}},\:..\right. \\ $$$$\mathrm{i}\:\mathrm{thought}\:\mathrm{midpoint}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{2}\:\mathrm{sir}.\:\:\mathrm{please}\:\mathrm{let}\:\mathrm{me}\:\mathrm{understand}\:\mathrm{sir} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

yes you are right...let me[rectify...

$${yes}\:{you}\:{are}\:{right}...{let}\:{me}\left[{rectify}...\right. \\ $$

Commented by Tawa1 last updated on 26/Dec/18

God bless you sir. I really appreciate your time sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com