Find x and y x^2 + y^2 = 25 ...... (i) x^3 + y^3 = 91 ....... (ii)


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 51431 by Tawa1 last updated on 26/Dec/18

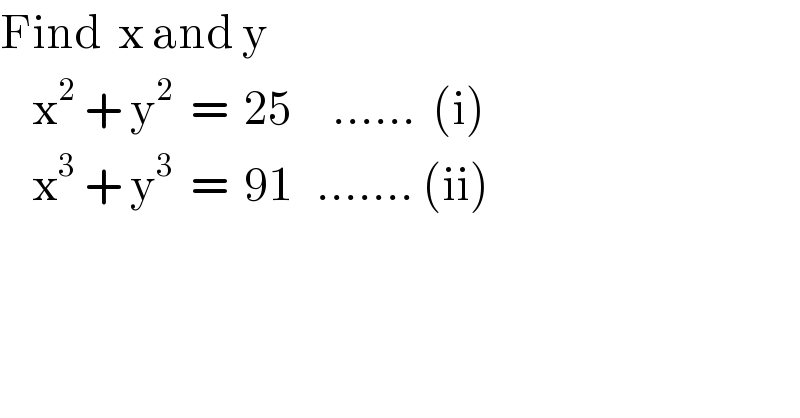
$Find x and y$ $x^{2} + y^{2} = 25 . . . . . . (i)$ $x^{3} + y^{3} = 91 . . . . . . . (ii)$
Commented by Tawa1 last updated on 27/Dec/18

$God bless you sir .$
Commented by Abdo msup. last updated on 26/Dec/18

$l e t x + y = s a n d x y = p w e h a v e s^{2} = x^{2} + y^{2} + 2 x y$ $= 25 + 2 p s l s o s^{3} = x^{3} + y^{3} + 3 x y (x + y)$ $= 91 + 3 s p \Rightarrow s^{2} - 2 p = 25 a n d s^{3} - 3 s p = 91 \Rightarrow$ $s^{3} - 2 p s = 25 s \Rightarrow s^{3} - 3 p s + p s = 25 s \Rightarrow$ $91 + p s = 25 s \Rightarrow (25 - p) s = 91 \Rightarrow$ ${(25 - p)}^{2} s^{2} = 91^{2} \Rightarrow {(25 - p)}^{2} (2 p + 25) = 91^{2} \Rightarrow$ $(p^{2} - 50 p + 25^{2}) (2 p + 25) = 91^{2} \Rightarrow$ $2 p^{3} + 25 p^{2} - 100 p^{2} - 50.25 p + 2 . 25^{2} p + 25^{3} = 91^{2} \Rightarrow$ $2 p^{3} - 75 p^{2} + 25^{3} - 91^{2} = 0 \Rightarrow$ $p^{3} - \frac{75}{2} p^{2} + \frac{25^{3} - 91^{2}}{2} = 0 w e m u s t s o l v e t h e$ $e q u a t i o n x^{3} + {a x}^{2} + b = 0 l e t u s e t h e c h a n g e m e n t$ $x = t - \frac{a}{3}$ $(e) \Leftrightarrow t^{3} - 3 t^{2} . \frac{a}{3} + 3 t . \frac{a^{2}}{9} - \frac{a^{3}}{27} + a (t^{2} - \frac{2 a t}{3} + \frac{a^{2}}{9}) + b = 0$ $\Rightarrow t^{3} - {a t}^{2} + \frac{a^{2} t}{3} - \frac{a^{3}}{27} + {a t}^{2} - 2 \frac{a^{2} t}{3} + \frac{a^{3}}{9} + b = 0 \Rightarrow$ $t^{3} - \frac{a^{2}}{3} t + \frac{2 a^{3}}{9} + b = 0 a f t e r w e u s e t h e c h s n g e m e n t$ $t = u + v . . . . b e c o n t i n u e d . . .$
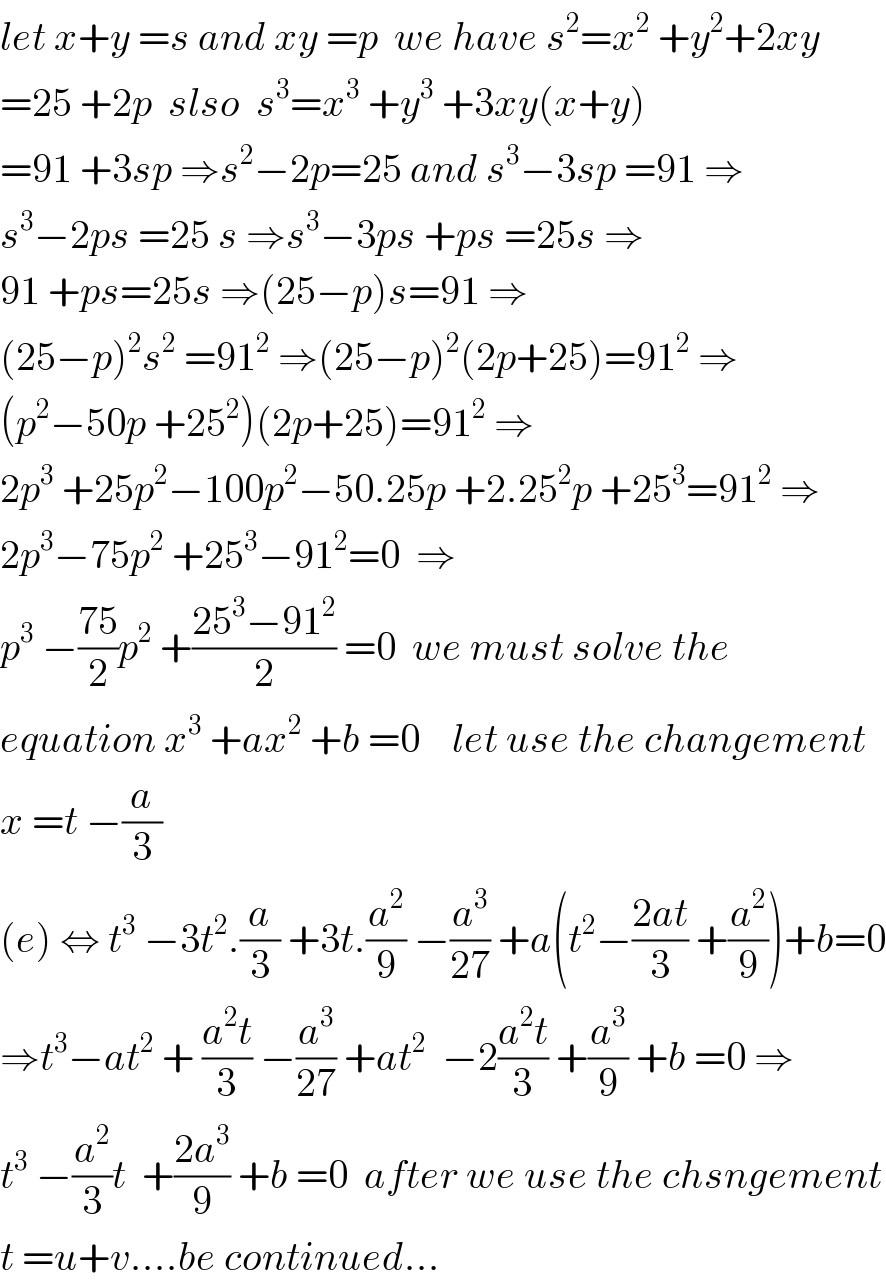
Commented by Abdo msup. last updated on 26/Dec/18

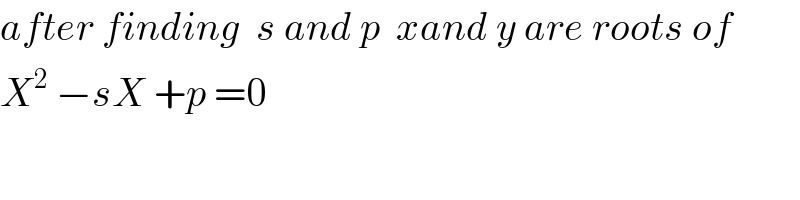
$a f t e r f i n d i n g s a n d p x a n d y a r e r o o t s o f$ $X^{2} - s X + p = 0$
	Answered by mr W last updated on 26/Dec/18

	$l e t x + y = a, x y = b$ $x^{3} + y^{3} = (x + y) (x^{2} + y^{2} - x y)$ $\Rightarrow 91 = (x + y) (25 - x y)$ $\Rightarrow 91 = a (25 - b) . . . (1)$ $x^{2} + y^{2} = {(x + y)}^{2} - 2 x y$ $\Rightarrow 25 = {(x + y)}^{2} - 2 x y$ $\Rightarrow 25 = a^{2} - 2 b . . . (2)$ $f r o m (2) :$ $\Rightarrow b = \frac{a^{2} - 25}{2}$ $91 = a (25 - \frac{a^{2} - 25}{2})$ $a^{3} - 75 a + 182 = 0$ $(a - 7) (a^{2} + 7 a - 26) = 0$ $\Rightarrow a = 7$ $\Rightarrow a = \frac{- 7 \pm \sqrt{153}}{2}$ $w i t h a = 7 :$ $b = \frac{49 - 25}{2} = 12$ $x, y a r e r o o t s o f$ $t^{2} - 7 t + 12 = 0$ $(t - 3) (t - 4) = 0$ $\Rightarrow x, y = 3, 4$ $w i t h a = \frac{- 7 - \sqrt{153}}{2}$ $\Rightarrow b = \frac{1 - 7 a}{2} = \frac{51 + 7 \sqrt{153}}{4}$ $x, y a r e r o o t s o f$ $t^{2} + \frac{7 + \sqrt{153}}{2} t + \frac{51 + 7 \sqrt{153}}{4} = 0$ $\Rightarrow x, y = \frac{1}{4} (- 7 - \sqrt{153} \pm i \sqrt{2 + 14 \sqrt{153}})$ $w i t h a = \frac{- 7 + \sqrt{153}}{2}$ $\Rightarrow b = \frac{1 - 7 a}{2} = \frac{51 - 7 \sqrt{153}}{4}$ $x, y a r e r o o t s o f$ $t^{2} + \frac{7 - \sqrt{153}}{2} t + \frac{51 - 7 \sqrt{153}}{4} = 0$ $\Rightarrow x, y = \frac{1}{4} (- 7 + \sqrt{153} \pm \sqrt{- 2 + 14 \sqrt{153}})$ $\Rightarrow x, y \approx - 1.928, 4.613$
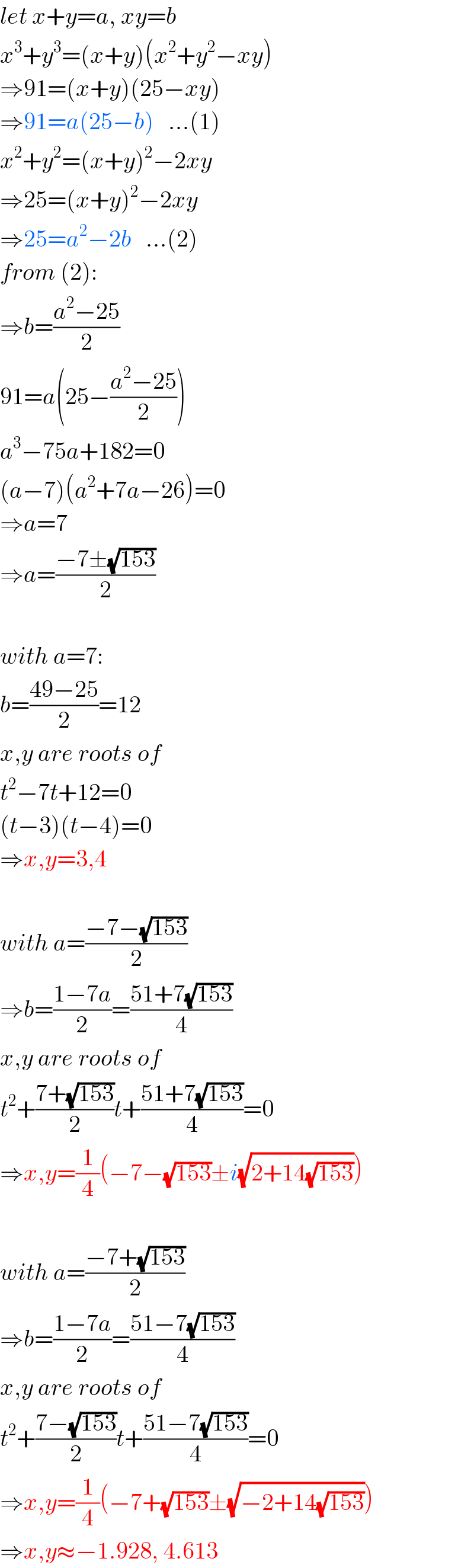
	Commented by Tawa1 last updated on 27/Dec/18

	$God bless you sir$
	Answered by peter frank last updated on 26/Dec/18

	$l e t$ $a = x^{2}$ $b = y^{2}$ $a + b = 25 . . . . (i) \times x$ $a x + b y = 91 . . . (i i)$ $a x + b x = 25 x$ $a x + b y = 91$ $b (x - y) = 25 x - 91 . . . (i i i)$ $a + b = 25 . . . . (i) \times y$ $a x + b y = 91 . . . (i i)$ $a y + b y = 25 y$ $a x + b y = 91$ $a (y - x) = 25 y - 91 . . . . (i v)$ $b (x - y) = 25 x - 91 . . . (i i i)$ $- a (x - y) = - 25 y + 91 . . . . (i v)$ $(x - y) [- a + b] = 25 (x - y)$ $b - a = 25 . . . . . . v$ $. . . .$
	Commented by Tawa1 last updated on 27/Dec/18

	$God bless you sir$
	Answered by behi83417@gmail.com last updated on 27/Dec/18
	$x+y=p,xy=q ⇒ { ((p^2 −2q=25)),((p(p^2 −3q)=91)) :}⇒ { ((3p^3 −6pq=75p)),((2p^3 −6pq=182)) :} ⇒p^3 −75p+182=0 ⇒(p−7)(p^2 +7p−26)=0 ⇒p=7,[((−7±(√(49+4×26)))/2)=2.68,−9.68] p=7⇒49−2q=25⇒q=12 p=2.68⇒7.18−2q=25⇒q=−8.91 p=−9.68⇒93.7−2q=25⇒q=34.35 1.[p=7,q=12]⇒z^2 −7z+12=0 ⇒[z_1 =x=3,z_2 =y=4]∨[x=4,y=3] 2.[p=2.68,q=−8.91]⇒z^2 −2.68z−8.91=0 ⇒[z_(1,2) =x∨y=((2.68±(√(2.68^2 +4×8.91)))/2)] ⇒[z_(1,2) =x∨y= 4.61 ∨−1.93] 3.[p=−9.69,q=34.35]⇒z^2 +9.69z+34.35=0 ⇒[z_(1,2) =((−9.69±(√(9.69^2 −4×34.35)))/2)] ⇒[z_(1,2) =x∨y=−4.85±3.3i] .■$
	$x + y = p, x y = q$ $\Rightarrow {\begin{cases} p^{2} - 2 q = 25 \\ p (p^{2} - 3 q) = 91 \end{cases} \Rightarrow {\begin{cases} 3 p^{3} - 6 p q = 75 p \\ 2 p^{3} - 6 p q = 182 \end{cases}$ $\Rightarrow p^{3} - 75 p + 182 = 0$ $\Rightarrow (p - 7) (p^{2} + 7 p - 26) = 0$ $\Rightarrow p = 7, [\frac{- 7 \pm \sqrt{49 + 4 \times 26}}{2} = 2.68, - 9.68]$ $p = 7 \Rightarrow 49 - 2 q = 25 \Rightarrow q = 12$ $p = 2.68 \Rightarrow 7.18 - 2 q = 25 \Rightarrow q = - 8.91$ $p = - 9.68 \Rightarrow 93.7 - 2 q = 25 \Rightarrow q = 34.35$ $1 . [p = 7, q = 12] \Rightarrow z^{2} - 7 z + 12 = 0$ $\Rightarrow [z_{1} = x = 3, z_{2} = y = 4] \lor [x = 4, y = 3]$ $2 . [p = 2.68, q = - 8.91] \Rightarrow z^{2} - 2.68 z - 8.91 = 0$ $\Rightarrow [z_{1, 2} = x \lor y = \frac{2.68 \pm \sqrt{2 . 68^{2} + 4 \times 8.91}}{2}]$ $\Rightarrow [z_{1, 2} = x \lor y = 4.61 \lor - 1.93]$ $3 . [p = - 9.69, q = 34.35] \Rightarrow z^{2} + 9.69 z + 34.35 = 0$ $\Rightarrow [z_{1, 2} = \frac{- 9.69 \pm \sqrt{9 . 69^{2} - 4 \times 34.35}}{2}]$ $\Rightarrow [z_{1, 2} = x \lor y = - 4.85 \pm 3.3 i] . ◼$
	Commented by Tawa1 last updated on 27/Dec/18

	$God bless you sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum