Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 51614 by peter frank last updated on 29/Dec/18

Prove that length of lactus rectum when directrix are parallel to y−axis is y_1 −y_2 =((2b^2 )/a)

$${Prove}\:{that}\:{length}\:{of} \\ $$$${lactus}\:{rectum}\:{when}\: \\ $$$${directrix}\:{are}\:{parallel}\:{to} \\ $$$${y}−{axis}\:{is}\: \\ $$$${y}_{\mathrm{1}} −{y}_{\mathrm{2}} =\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 29/Dec/18

for ellipse (x^2 /a^2 )+(y^2 /b^2 )=1 ditectrix is ∥ to yaxis focus(c,0) and (−c,0) so eqn of st line ∥to yaxis passing through (c,0) is x=c solve x=c and (x^2 /a^2 )+(y^2 /b^2 )=1 (y^2 /b^2 )=1−(c^2 /a^2 ) so y=±(b/a)(√(a^2 −c^2 )) now diztance between (c,(b/a)(√(a^2 −c^2 )) )and(c,((−b)/a)(√(a^2 −c^2 )) ) is=((2b)/a)(√(a^2 −c^2 )) [for ellipse c^2 =a^2 −b^2 ] =((2b)/a)×b=((2b^2 )/a) for hyperbola (x^2 /a^2 )−(y^2 /b^2 )=1 directrix is ∥ to yaxis focus(c,0) (−c,0) eqn of st line passing through(c,0) and ∥ to yaxis is x=c solve x=c and (x^2 /a^2 )−(y^2 /b^2 )=1 (y^2 /b^2 )=(c^2 /a^2 )−1 y=±(b/a)(√(c^2 −a^2 )) y=±(b/a)×b [for hyperbola c^2 =a^2 +b^2 ] y=±(b^2 /a) so latus rectum is ((2b^2 )/a)

$${for}\:{ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:{ditectrix}\:{is}\:\parallel\:{to}\:{yaxis} \\ $$$${focus}\left({c},\mathrm{0}\right)\:{and}\:\left(−{c},\mathrm{0}\right)\:\:{so}\:{eqn}\:{of}\:{st}\:{line}\:\parallel{to}\:{yaxis} \\ $$$${passing}\:{through}\:\left({c},\mathrm{0}\right)\:{is}\:{x}={c} \\ $$$${solve}\:{x}={c}\:\:{and}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}−\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:\:{so}\:{y}=\pm\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }\: \\ $$$${now}\:{diztance}\:{between}\:\left({c},\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\right){and}\left({c},\frac{−{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\right) \\ $$$${is}=\frac{\mathrm{2}{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\:\:\left[{for}\:{ellipse}\:{c}^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{2}{b}}{{a}}×{b}=\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}} \\ $$$${for}\:{hyperbola}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${directrix}\:{is}\:\parallel\:{to}\:{yaxis} \\ $$$${focus}\left({c},\mathrm{0}\right)\:\left(−{c},\mathrm{0}\right) \\ $$$${eqn}\:{of}\:{st}\:{line}\:{passing}\:{through}\left({c},\mathrm{0}\right)\:{and}\:\parallel\:{to}\:{yaxis} \\ $$$${is}\:{x}={c} \\ $$$${solve}\:{x}={c}\:{and}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{1} \\ $$$${y}=\pm\frac{{b}}{{a}}\sqrt{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }\: \\ $$$${y}=\pm\frac{{b}}{{a}}×{b}\:\:\left[{for}\:{hyperbola}\:{c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right] \\ $$$${y}=\pm\frac{{b}^{\mathrm{2}} }{{a}} \\ $$$${so}\:{latus}\:{rectum}\:{is}\:\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}} \\ $$$$ \\ $$

Commented by peter frank last updated on 29/Dec/18

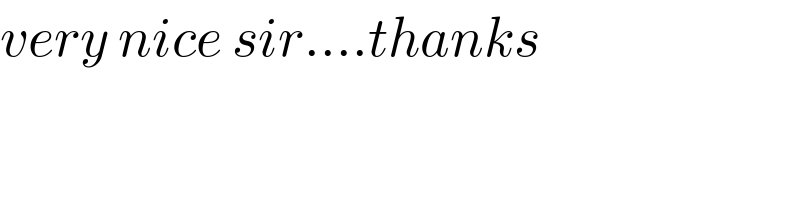
very nice sir....thanks

$${very}\:{nice}\:{sir}....{thanks} \\ $$

Answered by peter frank last updated on 29/Dec/18

(((x−h)^2 )/a^2 )−(((y−k)^2 )/b^2 )=1 x=h+ae(parallel to y−axis) (((h+ae−h)^2 )/a^2 )−(((y−k)^2 )/b^2 )=1 e^2 −1=(((y−k)^2 )/b^2 ) y−k=(√(b^2 (e^2 −1))) y−k=±b(√((e^2 −1))) y=k±b(√((e^2 −1))) y_(1 ) =k−b(√(e^2 −1)) ....(i) y_(2 ) =k+b(√(e^2 −1)) ....(ii) y_(2 ) −y_1 =−2b(√(e^2 −1)) y_(1 ) −y_2 =2b(√(e^2 −1)) from b^2 =a^2 (e^2 −1) y_(1 ) −y_2 =2b×(b/a) y_(1 ) −y_2 =((2b^2 )/a)

$$\frac{\left({x}−{h}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\left({y}−{k}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${x}={h}+{ae}\left({parallel}\:{to}\:{y}−{axis}\right) \\ $$$$\frac{\left({h}+{ae}−{h}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\left({y}−{k}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${e}^{\mathrm{2}} −\mathrm{1}=\frac{\left({y}−{k}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${y}−{k}=\sqrt{{b}^{\mathrm{2}} \left({e}^{\mathrm{2}} −\mathrm{1}\right)}\:\: \\ $$$${y}−{k}=\pm{b}\sqrt{\left({e}^{\mathrm{2}} −\mathrm{1}\right)}\:\: \\ $$$${y}={k}\pm{b}\sqrt{\left({e}^{\mathrm{2}} −\mathrm{1}\right)}\:\: \\ $$$${y}_{\mathrm{1}\:} ={k}−{b}\sqrt{{e}^{\mathrm{2}} −\mathrm{1}}\:....\left({i}\right) \\ $$$${y}_{\mathrm{2}\:} ={k}+{b}\sqrt{{e}^{\mathrm{2}} −\mathrm{1}}\:....\left({ii}\right) \\ $$$${y}_{\mathrm{2}\:} −{y}_{\mathrm{1}} =−\mathrm{2}{b}\sqrt{{e}^{\mathrm{2}} −\mathrm{1}}\: \\ $$$${y}_{\mathrm{1}\:} −{y}_{\mathrm{2}} =\mathrm{2}{b}\sqrt{{e}^{\mathrm{2}} −\mathrm{1}}\: \\ $$$${from} \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} \left({e}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${y}_{\mathrm{1}\:} −{y}_{\mathrm{2}} =\mathrm{2}{b}×\frac{{b}}{{a}} \\ $$$${y}_{\mathrm{1}\:} −{y}_{\mathrm{2}} =\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com